- Adäquatheitssatz
-
Adäquatheit bezeichnet in der Logik die Eigenschaft eines Kalküls, vollständig und korrekt zu sein. Adäquatheit ist eine Beziehung zwischen einem semantisch definierten Folgerungsoperator
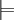 und einem syntaktisch definierten Herleitungsoperator
und einem syntaktisch definierten Herleitungsoperator 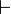 , die besagt, dass alles, was syntaktische hergeleitet werden kann, auch semantisch gefolgert werden kann, und umgekehrt:
, die besagt, dass alles, was syntaktische hergeleitet werden kann, auch semantisch gefolgert werden kann, und umgekehrt: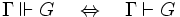
Das bedeutet, dass „sich die Begriffe der Beweisbarkeit und der Ableitbarkeit im Kalkül mit den jeweiligen Begriffen der Allgemeingültigkeit und der logischen Folgerung decken“.[1] Jede Tautologie ist dann also auch ein Theorem, und umgekehrt.
Quellen
- ↑ Hoyningen-Huene, Logik (1998), S. 270
Wikimedia Foundation.
