- Ehrenfeucht-Fraisse Spiel
-
Ehrenfeucht-Fraïssé-Spiele (EF-Spiele) sind eine Beweistechnik der Modelltheorie. Durch EF-Spiele lässt sich die Äquivalenz zweier Strukturen zeigen bzw. widerlegen. Strukturen dienen in der beschreibenden Komplexitätstheorie meist als Formalismus zur Beschreibung von Objekten wie Wörtern oder Graphen. Ehrenfeucht-Fraïssé-Spiele liefern so ein Hilfsmittel zum Beweisen von unteren Schranken, also zum Beweis, dass sich eine gegebene Klasse von Strukturen nicht durch eine bestimmte Logik ausdrücken lässt.
Entwickelt wurden sie von Andrzej Ehrenfeucht auf Grundlage der theoretischen Arbeit des Mathematikers Roland Fraïssé.
Ein EF-Spiel wird von zwei Spielern gespielt, gewöhnlich bezeichnet mit Spoiler und Duplicator (nach Joel Spencer) oder Samson und Delilah (nach Neil Immerman) [1].
Inhaltsverzeichnis
Bezeichnungen
- Sei
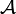 eine Struktur. Dann bezeichne
eine Struktur. Dann bezeichne 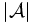 das entsprechende Universum (Grundmenge, Trägermenge).
das entsprechende Universum (Grundmenge, Trägermenge). - STRUKT[σ] bezeichne die Menge aller endlichen Strukturen der Signatur σ.
Das n-Runden-EF-Spiel
Ehrenfeucht-Fraïssé-Spiele in ihrer herkömmlichen Form haben einen engen Bezug zu Logiken erster Stufe. Diese Grundform ist wie folgt definiert.
Definition
Seien
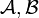 zwei Strukturen der gleichen Signatur,
zwei Strukturen der gleichen Signatur,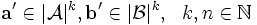 .
.
Ein n-Runden-Spiel wird auf den Interpretationen
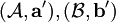 definiert:
definiert:- Das EF-Spiel
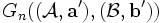 hat n Runden, die Ausgangsmenge ist
hat n Runden, die Ausgangsmenge ist 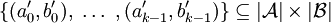 ;
;
-
- in jeder Runde i (i<n) wählt zunächst Samson ein beliebiges
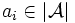 oder ein
oder ein 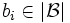 , welches noch nicht zuvor gewählt wurde
, welches noch nicht zuvor gewählt wurde - falls Samson ein Element aus
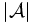 gewählt hat, wählt daraufhin Delilah auf dieselbe Weise ein beliebiges
gewählt hat, wählt daraufhin Delilah auf dieselbe Weise ein beliebiges 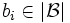 , sonst ein
, sonst ein 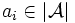
- das resultierende Tupel (ai,bi) wird zur Ausgangsmenge hinzugefügt.
- in jeder Runde i (i<n) wählt zunächst Samson ein beliebiges
- Nach n Runden resultiert eine Menge von 2-Tupeln
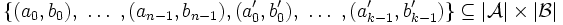 .
.
- Falls durch diese Menge ein partieller Isomorphismus
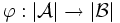 definiert wird, hat Delilah gewonnen, ansonsten hat Samson gewonnen.
definiert wird, hat Delilah gewonnen, ansonsten hat Samson gewonnen.
- Falls durch diese Menge ein partieller Isomorphismus
- Per Definition gewinnt Delilah das Spiel
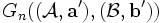 , falls sie eine zwingende Gewinnstrategie hat.
, falls sie eine zwingende Gewinnstrategie hat.
Oft gilt k = 0; man schreibt
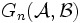 und die Ausgangsmenge ist leer.
und die Ausgangsmenge ist leer.Eigenschaften von EF-Spielen
Satz
Zwei Strukturen
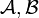 sind n-äquivalent,
sind n-äquivalent, 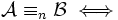 Delilah gewinnt
Delilah gewinnt 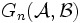 .
.Korollar
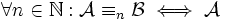 und
und 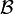 sind elementar äquivalent.
sind elementar äquivalent.Beweisen von unteren Schranken
Um zu beweisen, dass eine Menge I ⊆ STRUKT[σ] nicht durch FO[σ]-Formeln definiert werden kann, genügt es zu zeigen, dass es für jedes n ∈
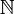 zwei Strukturen
zwei Strukturen 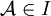 und
und ![\mathcal{B} \in STRUKT[\sigma]\setminus I](/pictures/dewiki/56/87b3539ebb091429b54e77020f212ad3.png) gibt, so dass Delilah eine Gewinnstrategie für
gibt, so dass Delilah eine Gewinnstrategie für 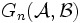 hat.
hat.EF-Spiele für die Prädikatenlogik zweiter Stufe
Ehrenfeucht-Fraïssé-Spiele können relativ problemlos auf Logiken zweiter Stufe erweitert werden. Das Beweisen von Gewinnstrategien wird hierbei jedoch deutlich schwieriger. Eine eingeschränkte Variante sind Spiele für die existentielle Prädikatenlogik zweiter Stufe (SO∃, ESO). SO∃ spielt durch die Charakterisierung der Komplexitätsklasse NP eine wichtige Rolle in der beschreibenden Komplexitätstheorie.
Beschränkt man die SO∃-Logik weiter auf monadische Prädikate (MSO∃), so ist diese Version der EF-Spiele äquivalent zu den Ajtai-Fagin-Spielen [2].
SO∃-Spiele
Definition
Seien
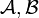 zwei Strukturen der gleichen Signatur
zwei Strukturen der gleichen Signatur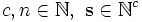
die Eingaben für ein SO∃-Spiel.
- Samson wählt die c Prädikate
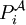 der Stelligkeit si über
der Stelligkeit si über 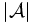
- Delilah wählt daraufhin die c Prädikate
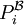 der Stelligkeit si über
der Stelligkeit si über 
- Auf der beiden erweiterten Strukturen wird schließlich das Ehrenfeucht-Fraïssé-Spiel
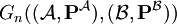 gespielt.
gespielt.
Bei MSO∃-Spielen (Beschränkung auf monadische Prädikate) gilt si = 1 für alle i.
Ajtai-Fagin-Spiele
Ajtai-Fagin-Spiele sind in dem Sinne äquivalent zu den MSO∃-Spielen, als dass Delilah das Ajtai-Fagin-Spiel auf einer Menge I ⊆ STRUKT[σ] gewinnt, genau dann, wenn es für jedes c und jedes n zwei Strukturen
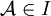 und
und ![\mathcal{B} \in STRUKT[\sigma]\setminus I](/pictures/dewiki/56/87b3539ebb091429b54e77020f212ad3.png) gibt, so dass sie das entsprechende MSO∃-Spiel gewinnt. Ajtai-Fagin-Spiele sind jedoch formal leichter handhabbar als MSO∃-Spiele.
gibt, so dass sie das entsprechende MSO∃-Spiel gewinnt. Ajtai-Fagin-Spiele sind jedoch formal leichter handhabbar als MSO∃-Spiele.Definition
Ein Ajtai-Fagin-Spiel wird auf einer Menge von Strukturen I ⊆ STRUKT[σ] gespielt:
- Zuerst wählt Samson zwei Zahlen
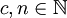
- Delilah wählt daraufhin eine Struktur
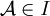
- Samson wählt die monadischen Prädikate
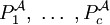 über
über 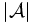
- Delilah wählt nun eine weitere Struktur
![\mathcal{B} \in STRUKT[\sigma]\setminus\emph{I}](/pictures/dewiki/49/1fbbc17e42a4c782d0649dce82c1039a.png) sowie die monadischen Prädikate
sowie die monadischen Prädikate 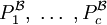 über
über 
- Nun wird auf den beiden erweiterten Strukturen das Ehrenfeucht-Fraïssé-Spiel
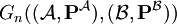 gespielt
gespielt
Satz
Sei I ⊆ STRUKT[σ].
Delilah gewinnt das Ajtai-Fagin-Spiel auf I
 I ist nicht durch MSO∃[σ]-Logik definierbar.
I ist nicht durch MSO∃[σ]-Logik definierbar.Referenzen
- ↑ Stanford Encyclopedia of Philosophy, Logic and Games.
- ↑ Neil Immerman: Descriptive Complexity. Springer, ISBN 978-0387986005
- Sei
Wikimedia Foundation.
