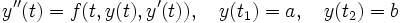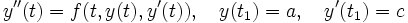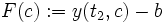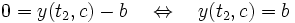- Einzelschießverfahren
-
Das Schießverfahren ist eine numerische Methode, um Randwertprobleme gewöhnlicher Differentialgleichungen zu lösen. Die Grundidee des Verfahrens besteht darin, das Problem auf die Lösung eines Anfangswertproblems zurückzuführen.
Das Verfahren erinnert an eine Methode, mit einem Geschoss ein entferntes Ziel zu treffen. Das Geschoss wird mit einer bestimmten Anfangssteigung abgefeuert. Diese Anfangssteigung variiert man solange, bis man das Ziel trifft. Daher rührt die Bezeichnung Schießverfahren.
Das Randwertproblem zweiter Ordnung mit gesuchter Funktion
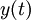 und rechter Seite f
und rechter Seite fwird umformuliert in ein Anfangswertproblem
Der zweite, unbekannte Anfangswert c ist frei wählbar. Das Anfangswertproblem wird so lange in Abhängigkeit vom Parameter c integriert, bis die Bedingung am anderen Rand
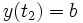 erfüllt ist. Die Lösung
erfüllt ist. Die Lösung 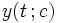 des Anfangswertproblems kann dabei mit einem numerischen Verfahren, z. B. Runge-Kutta gelöst werden.
des Anfangswertproblems kann dabei mit einem numerischen Verfahren, z. B. Runge-Kutta gelöst werden. 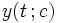 ist abhängig vom Anfangswert c. Definiere dazu eine Funktion F
ist abhängig vom Anfangswert c. Definiere dazu eine Funktion FDieses oft nichtlineare Gleichungssystem kann numerisch zum Beispiel mit dem Newton-Verfahren oder dem Bisektionsverfahren gelöst werden. Die Lösung des Anfangswertproblems ist genau dann eine Lösung des Randwertproblems, wenn F in c eine Nullstelle hat:
In der Praxis verwendet man aus Stabilitätsgründen die sogenannte Mehrzielvariante des Schießverfahrens, bei dem stückweise Lösungen in Teilintervallen eines Gitters
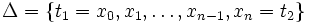 berechnet werden, aus denen sich anschließend die Lösung in [a,b] zusammensetzt.
berechnet werden, aus denen sich anschließend die Lösung in [a,b] zusammensetzt.Literatur
- J. Stoer, R. Bulirsch: Introduction to Numerical Analysis. Springer, New York 1980
- A. Willers: Methoden der praktischen Analysis. 2. Auflage. De Gruyter, Berlin 1950
- L. Collatz: Numerische Behandlung von Differentialgleichungen. Springer, Berlin 1951
- M. Hermann: Numerik gewöhnlicher Differentialgleichungen. Anfangs- und Randwertprobleme, Oldenbourg Wissenschaftsverlag München und Wien 2004, ISBN 3-486-27606-9
Wikimedia Foundation.