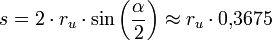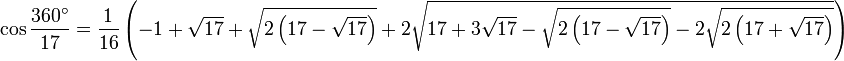17-Eck

regelmäßiges Siebzehneck

Das Siebzehneck (Heptadekagon) ist eine geometrische Figur, die zur Gruppe der Vielecke (Polygone) gehört. Es ist definiert durch siebzehn Punkte, welche durch siebzehn Strecken zu einem geschlossenen Linienzug verbunden sind. Hier geht es um das regelmäßige Siebzehneck, welches siebzehn gleichlange Seiten hat und dessen Ecken auf einem gemeinsamen Umkreis liegen.

Eigenschaften

Der Zentriwinkel α hat einen Wert von $\frac{360^\circ}{17} \approx 21{,}17647059^\circ$.

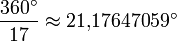Das Verhältnis der Länge einer Seite zum Umkreisradius beträgt:

$s = 2 \cdot r_u \cdot \sin \left( \frac{\alpha}{2} \right) \approx r_u \cdot 0{,}3675$

Das Besondere an einem regelmäßigen Siebzehneck ist die Tatsache, dass es konstruierbar ist, d. h., es kann unter alleiniger Verwendung von Zirkel und Lineal (den Euklidischen Werkzeugen) gezeichnet werden. Dies wurde von Carl Friedrich Gauß im Jahre 1796 nachgewiesen. Er zeigte, dass der Kosinus des Zentriwinkels der Formel

$\cos \frac{360^\circ}{17} = \frac{1}{16} \left( -1 + \sqrt{17} + \sqrt{ 2 \left(17- \sqrt{17} \right)} + 2 \sqrt{ 17 + 3 \sqrt{17} - \sqrt{2 \left(17- \sqrt{17} \right)} - 2 \sqrt{2 \left(17+ \sqrt{17} \right)} } \right)$

entspricht, woraus sich die Konstruierbarkeit ergibt.

Im Jahre 1825 veröffentlichte Johannes Erchinger erstmalig eine Konstruktionsanleitung für das regelmäßige Siebzehneck in 64 Schritten. Eine animierte Darstellung dieser Konstruktion folgt weiter unten.

Konstruktion

Exakte Konstruktion

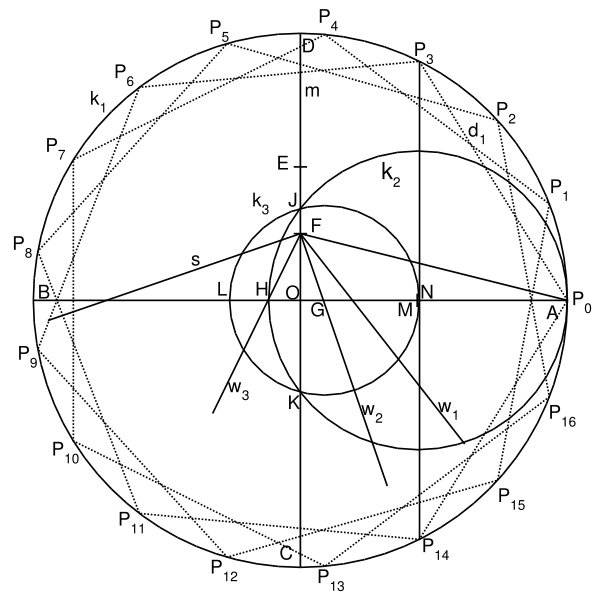
1. Zeichnen eines großen Kreises k₁ (des späteren Umkreises des entstehenden Siebzehnecks) um O,
2. Zeichnen eines Durchmessers AB,
3. Konstruktion der Mittelsenkrechten m, welche k₁ in C und D schneidet,
4. Konstruktion des Mittelpunktes E von DO,
5. Konstruktion des Mittelpunktes F von EO und Zeichnen von FA,
6. Konstruktion der Winkelhalbierenden w₁ des Winkels OFA,
7. Konstruktion der Winkelhalbierenden w₂ des Winkels zwischen m und w₁, Schnittpunkt mit AB ist Punkt G.
8. Konstruktion der Senkrechten s zu w₂ auf dem Punkt F,
9. Konstruktion der Winkelhalbierenden w₃ zwischen s und w₂. Schnittpunkt mit AB ist Punkt H.
10. Konstruktion des Thaleskreises k₂ über HA. Die Schnittpunkte mit CD sind J und K.
11. Konstruktion eines Kreises k₃ um G, der durch J und K verläuft. Die Schnittpunkte mit AB sind die Punkte L und N (dabei liegt N sehr nahe am Mittelpunkt M von k₂).
12. Konstruktion einer Tangente zu k₃ durch N.

Die Schnittpunkte dieser Tangente mit dem Ausgangskreis k₁ sind die Punkte P₃ und P₁₄ des regelmäßigen Siebzehnecks. Mit A = P₀ lassen sich durch je siebenmaliges Abtragen des Abstandes d₁ in jede Richtung auf dem Kreis alle weiteren Punkte des Siebzehnecks finden.

Variation:

1. bis 5. wie vorher

6. Konstruktion der Winkelhalbierenden w1 des Winkels OFA, Schnittpunkt mit AB ist Punkt Q.

7. Konstruktion eines Kreises k4 um Q, der durch F verläuft, Schnittpunkt von k4 mit AB ist H.

Weiter mit Schritt 10 der vorherigen Konstruktion.

Animation der Konstruktion Erchingers

Konstruktion des Siebzehnecks mit Zirkel und Lineal in 64 Schritten nach Johannes Erchinger

Literatur

• Karin Reich: Die Entdeckung und frühe Rezeption der Konstruierbarkeit des regelmäßigen 17-Ecks und dessen geometrische Konstruktion durch Johannes Erchinger (1825). In: Mathesis, Festschrift zum siebzigsten Geburtstag von Matthias Schramm. Hrsg. von Rüdiger Thiele, Berlin, Diepholz 2000, S. 101-118.

Weblinks

• Das Siebzehneck auf www.mathworld.com (englisch)