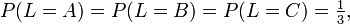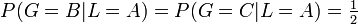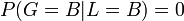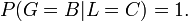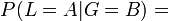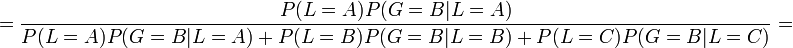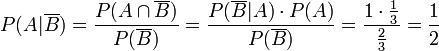Gefangenenparadox

Das Gefangenenparadoxon ist ein Paradoxon über bedingte Wahrscheinlichkeiten und die Bayesformel. Es ist nicht zu verwechseln mit dem Gefangenendilemma der Spieltheorie.

Formulierung des Problems

„In einem Gefängnis sitzen drei zum Tode verurteilte Gefangene: Anton, Brigitte und Clemens. Genau einer von ihnen soll begnadigt werden. Dazu wird ein Los gezogen, das allen die gleiche Chance gibt, begnadigt zu werden. Der Gefangene Anton, der also eine Überlebenswahrscheinlichkeit von 1/3 hat, bittet den Wärter, der das Ergebnis des Losentscheids kennt, ihm einen seiner Leidensgenossen Brigitte oder Clemens zu nennen, der oder die sterben muss. Der Wärter antwortet ‚Brigitte‘. Wie hoch ist nun Antons Überlebenswahrscheinlichkeit?“

Die Lösung ist: die Wahrscheinlichkeit bleibt 1/3.

In mathematischen Formeln sieht das so aus: Man setze Ω = {A,B,C} nach den Anfangsbuchstaben der Akteure, und hierauf die Zufallsvariable L, die den Losentscheid darstellt, und auf Ω abbildet. Es gilt

$P(L=A) = P(L=B) = P(L=C) = \tfrac13,$

das heißt: L ist gleichverteilt. Weiterhin sei G eine Zufallsvariable die angibt, wen der Wärter nennt, es gilt als Teil der Aufgabe:

$P(G=B|L=A) = P(G=C|L=A) = \tfrac 12$

$\!\,P(G=B|L=B)=0$

und

$\!\,P(G=B|L=C)=1.$

Die Überlebenswahrscheinlichkeit für Anton ist also nach der Bayesformel:

$\!\,P(L=A|G=B) =$

$={P(L=A) P(G=B|L=A) \over P(L=A) P(G=B|L=A) + P(L=B)P(G=B|L=B) + P(L=C) P(G=B|L=C)} =$

$= \frac{\frac{1}{3} \cdot \frac{1}{2}}{\frac{1}{3} \cdot \frac{1}{2} + \frac{1}{3} \cdot 0 + \frac{1}{3} \cdot 1} = \tfrac{1}{3}$.

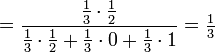Paradox

Das Paradoxe an dem Ergebnis ist, dass Antons Überlebenschance noch immer 1/3 ist, obwohl jetzt nur noch er und Clemens zur Debatte stehen. Die Überlebenswahrscheinlichkeit von Clemens ist jedoch auf 2/3 gestiegen.

Äquivalenz mit dem Ziegenproblem

Es liegt dem Gefangenenproblem derselbe Sachverhalt zugrunde wie dem Ziegenproblem. Dabei sind die Ereignisse der Begnadigung mit denen der Existenz des Gewinnes hinter einem Tor zu identifizieren, weiter das Öffnen eines Tores mit der Nennung eines Opfers und der Wärter mit dem Moderator. Wissen und Verhalten des Wärters ist dem des Moderators äquivalent. Im Moderator oder Wärter wird bloß das Verhalten der Wahrscheinlichkeiten subsumiert.

Anschauliche Lösung

Etwas verständlicher wird dies, wenn man 100 Gefangene betrachtet, von denen einer begnadigt werden soll. Antons Überlebenschancen als einer der Hundert liegen bei 1% und die Wahrscheinlichkeit, dass jemand anderes überlebt, beträgt 99%. Anton bittet den Wärter, 98 Sterbekandidaten aus den übrigen 99 zu nennen. Nach Abschluss der Aufzählung bleiben Clemens und Anton selbst übrig. Man kann nun argumentieren, dass in der neuen Situation Antons Wahrscheinlichkeit zu überleben durch das Aufzählen der Namen nicht erhöht worden ist. Und weil Clemens als einziger nicht genannt wurde, ist es sehr wahrscheinlich, dass er begnadigt wurde. Die Überlebenswahrscheinlichkeit von Anton beträgt weiterhin 1%, die von Clemens erhöht sich auf 99%.

Durch die Nennung eines Opfers gewährt der Wärter dem Fragenden neue Informationen. Jedoch betrifft diese Information nicht die Gewinnwahrscheinlichkeit des Fragenden. Der Wärter nennt einen vom Fragenden und vom Gewinner verschiedenen Gefangenen. Damit sind die Gefangenen in zwei Gruppen zu unterteilen, in die Gruppe des Fragenden und in eine Restgruppe. Die Informationsgebung des Wärters betrifft nur die Restmenge. Mit jedem Namen fällt die Gewinnwahrscheinlichkeit des genannten Opfers auf Null und die Gewinnwahrscheinlichkeit der Übrigen steigt entsprechend an, während die des Fragenden gleich bleibt.

Man nimmt an, dass die Auswahl-Wahrscheinlichkeit eines jeden Gefangenen zunächst gleich sei. Die Wahrscheinlichkeit, dass der Gewinner Element der Fragenden oder der Restmenge ist, steht durch die Verteilung der Zufallsvariablen fest.

Zusatz zu den obigen Überlegungen

„Nachdem also Anton die Antwort des Wärters bekommen hat, besucht der Wärter Clemens. Clemens fragt den Wärter, was dieser bei Anton gemacht habe. Der Wärter erzählt ihm die Geschichte. Worauf nun Clemens antwortet: Gott sei Dank habe ich nicht zuerst gefragt!“

Tatsächlich wäre bei der gleichen Antwort ‚Brigitte‘ die Gewinnchancen von Anton auf 2/3 gestiegen, während sie beim fragenden Clemens bei 1/3 geblieben wäre.

Das Paradox liegt darin, dass scheinbar die Gewinnchancen dessen steigen, der nicht gefragt hat. Natürlich bleiben die Gewinnchancen unabhängig der Fragerei gleich, nämlich bei 1/3. (Die Antwort auf die Frage erhöht nur die Information zu den Gewinnchancen der Gefangenen in der Restmenge.)

Betrachten wir noch die Frage: „Wie hoch ist die Wahrscheinlichkeit dafür, dass Anton begnadigt wurde unter der Bedingung, dass Brigitte nicht begnadigt wurde?“

Zunächst gelten die folgenden Wahrscheinlichkeiten:

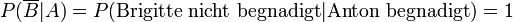$P(\overline B|A) = P(\text{Brigitte nicht begnadigt}|\text{Anton begnadigt}) = 1$ (Wenn Anton begnadigt ist, kann Brigitte nicht begnadigt sein)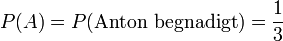

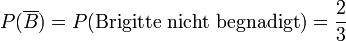
$P(A) = P(\text{Anton begnadigt}) = \frac{1}{3}$

$P(\overline B) = P(\text{Brigitte nicht begnadigt}) = \frac{2}{3}$

Das Ergebnis folgt dann unmittelbar aus der Definition der bedingten Wahrscheinlichkeit:

$P(A|\overline B) = \frac{P(A \cap \overline B)}{P(\overline B)} = \frac {P(\overline B|A) \cdot P(A)} {P(\overline B)} = \frac {1 \cdot \frac{1}{3}} {\frac{2}{3}} = \frac{1}{2}$

Nun haben wir zwei Lösungen, die sich scheinbar widersprechen. Was ist der Grund dafür?

Der Grund ist, dass die Antworten unter unterschiedlichen Bedingungen stattfinden. In der Fragestellung wird die Antwort des Wärters von der vorher stattgefundenen Auswahl (oben in der Trennung in Fragender und Restmenge) beeinflusst. Wird dieser Einfluss nicht mit berücksichtigt, gehen Informationen verloren, und das spiegelt sich in der Verschiebung der Wahrscheinlichkeit wider. (In der letzten Fragestellung wird keine Trennung der Gruppen vorgenommen, so kommt der Verlust der Gewinnchancen von Brigitte, den Gewinnchancen Anton und Clemens gleichermaßen zugute.)

Siehe auch

Verwandte Themen, bei denen man aus Teilinformation die optimale Entscheidung des Restproblems treffen kann:

• Odds-Strategie
• Sekretärinnenproblem
• Umtauschparadoxon
• Ziegenproblem
• Zwei-Zettel-Spiel