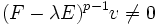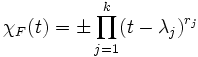- Hauptvektor
-
Der Hauptraum ist ein Begriff aus der linearen Algebra und eine Verallgemeinerung des Eigenraums. Haupträume spielen eine große Rolle beim Aufstellen der jordanschen Normalform und der Berechnung einer zugehörigen Basis.
Inhaltsverzeichnis
Definition des Hauptraums
Ist
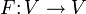 eine lineare Abbildung aus einem endlichdimensionalen Vektorraum V in sich selbst, λ ein Eigenwert von F und bezeichnet r die algebraische Vielfachheit des Eigenwertes λ, dann nennt man den Kern der r-fachen Hintereinanderausführung von (F − λ) Hauptraum zum Eigenwert λ, d. h.
eine lineare Abbildung aus einem endlichdimensionalen Vektorraum V in sich selbst, λ ein Eigenwert von F und bezeichnet r die algebraische Vielfachheit des Eigenwertes λ, dann nennt man den Kern der r-fachen Hintereinanderausführung von (F − λ) Hauptraum zum Eigenwert λ, d. h.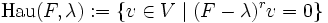 .
.
Der Hauptraum wird also von genau den Vektoren v aufgespannt, für die (F − λ)rv = 0 gilt. Insbesondere ist der Eigenraum zu einem Eigenwert ein Unterraum des Hauptraums zu diesem Eigenwert.
Hauptvektor
Die Elemente des Hauptraums werden manchmal auch Hauptvektoren genannt. Diesen Hauptvektoren kann man eine Stufe oder einen Level zuordnen. Sei F ein Endomorphismus und λ ein Eigenwert des Endomorphismus. Ein Vektor v heißt Hauptvektor der Stufe p, wenn
- (F − λE)pv = 0
aber
gilt. Die Eigenvektoren sind somit Hauptvektoren der Stufe 1.
Sei vp − 1 ein Hauptvektor der Stufe p − 1, so kann man den Hauptvektor der Stufe p berechnen, indem man das lineare Gleichungssystem
- (F − λE)vp = vp − 1
löst.
Satz über die Hauptraumzerlegung
Es sei F ein Endomorphismus, und sein charakteristisches Polynom
zerfalle vollständig in Linearfaktoren mit paarweise verschiedenen
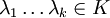 . Dann gilt:
. Dann gilt:- Der Hauptraum ist F-invariant, das heißt
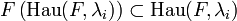 .
. - Die Dimensionen der Haupträume stimmen mit den Vielfachheiten der Nullstellen des charakteristischen Polynoms überein, also
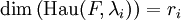 .
. - Die Haupträume bilden eine direkte Zerlegung von V. Es gilt also
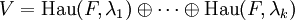 .
. - Der Endomorphismus F besitzt eine Zerlegung F = FD + FN. Darin ist FD diagonalisierbar, FN ist nilpotent, und es gilt
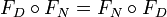 .
.
Literatur
- Gerd Fischer: Lineare Algebra, Vieweg-Verlag, ISBN 3-528-97217-3.
Wikimedia Foundation.