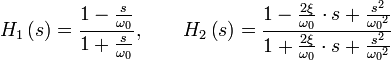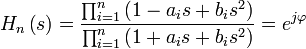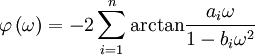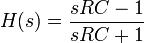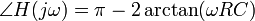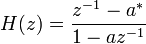- Allpass
-
Ein Allpassfilter, auch nur Allpass genannt, ist ein elektrisches Filter, das im Idealfall für alle Frequenzen einen konstanten Betragsfrequenzgang aufweist, während die Phasenverschiebung von der Frequenz abhängt. Allpässe werden unter anderem in nachrichtentechnischen Systemen zur Signalentzerrung verwendet.
Inhaltsverzeichnis
Allgemeines
Allpässe weisen eine frequenzabhängigen Gruppenlaufzeit auf, welche zur frequenzabhängigen Signalverzögerung bzw. der Phasenentzerrung verwendet werden kann. Es können damit frequenzabhängige und meist unerwünschte Signalverzögerungen in Übertragungskanälen kompensiert werden. Da die Gruppenlaufzeit die negative Ableitung des Phasenganges ist, ist diese nicht konstant und hängt von der Frequenz ab. Mit Hilfe von Allpässen kann auch eine Impedanztransformation durchgeführt werden.
Weiters werden Allpässe zur Hilberttransformation eingesetzt, um aus einem reellwertigen Signal ein analytisches Signal zu erzeugen. Bei der Hilberttransformation wird das Spektrum eines Signals in einem bestimmten Frequenzband um π/2 (90°) in der Phase gedreht. Jene Allpässe werden auch als „Hilbert-Transformator“ bezeichnet und werden, da sie in analogen elektrischen Schaltungen nur mit größeren Aufwand zu realisieren sind, bevorzugt im Bereich der digitalen Signalverarbeitung eingesetzt.
Allpässe können als passives Filter, als analoges aktives Filter oder im Rahmen der digitalen Signalverarbeitung als zeitdiskretes digitales Filter realisiert werden.
Allgemein weisen Allpässe folgende Beziehungen auf:
- Ein Allpass der Ordnung n hat n-Phasendrehungen entlang der Frequenzachse.
- Ein nicht minimalphasiges System kann in ein minimalphasiges Teilsystem und in einen Allpass aufgeteilt werden.
Pol- und Nullstellen
Die Übertragungsfunktion kontinuierlicher Allpässe, wie sie in Form analoger Schaltungen realisiert werden, haben in Paaren auftretende Null- und Polstellen im Pol-Nullstellen-Diagramm, die symmetrisch zur vertikalen jω-Achse in der s-Ebene liegen. Dabei liegen alle Nullstellen auf der rechten Halbebende (RHE), was den nicht minimalphasigen Phasengang bewirkt.
Bei zeitdiskreten Allpässen, angewendet im Bereich der digitalen Signalverarbeitung, liegen nach Anwendung der Z-Transformation alle Pole innerhalb und alle Nullstellen außerhalb des Einheitskreises in der komplexen Z-Ebene. Die Pol- und Nullstellen treten dabei paarweise gespiegelt am Einheitskreis auf.
Allpässe sind im Allgemeinen mit komplexen Filterkoeffizienten zu entwerfen. Bei dem Spezialfall reller Koeffizienten fallen die Pol- und Nullstellen auf der jω-Achse der s-Ebene bzw. am Einheitskreis in der z-Ebene zusammen.
Übertragungsfunktion
Die Übertragungsfunktion H1(s) eines zeitkontinulierlichen Allpasses 1. Ordnung bzw. H2(s) eines Allpasses 2. Ordnung ist:
Höhere Ordnungen entstehen, indem weitere Paare von Pol-Nullstellen zur Übertragungsfunktion hinzufügt werden. Ein Allpasss n-ter Ordnung ist gegeben durch:
mit den allgemeinen Koeffizienten ai und bi. Die im zweiten Ausdruck auftretende Phasenverschiebung φ ist eine Funktion der Kreisfrequenz ω mit s = j·ω mit folgendem Bezug:
Da der Frequenzgang idealerweise konstant ist, macht die Festlegung einer 3-dB-Grenzfrequenz im Betragsfrequenzgang keinen Sinn. Allpässe werden über die Gruppenlaufzeit Tgr als Funktion der Kreisfrequenz ω charakterisiert. Als Grenzfrequenz wird dabei üblicherweise das Absinken der Gruppenlaufzeit auf das
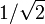 im Bezug zu dem Grenzwert der Gruppenlaufzeit bei der Frequenz 0 Hz festgelegt.
im Bezug zu dem Grenzwert der Gruppenlaufzeit bei der Frequenz 0 Hz festgelegt.Arten
Aktive analoge Implementierung
In nebenstehender Abbildung ist ein aktiver, analoger Allpass 1. Ordnung mit einem Operationsverstärker dargestellt. Seine Übertragungsfunktion (s = σ + j·ω) ist gegeben als:
mit einem Pol bei −1/RC und einer Nullstelle bei 1/RC. Der Phasengang als Funktion der Kreisfrequenz ω mit σ = 0 weist bei dieser Schaltung folgenden Verlauf auf:
Ein Vorteil der Realisierung mittels Operationsverstärkern besteht darin, dass in der Schaltung keine Spulen eingesetzt werden.
Passive analoge Implementierung
Passive Allpassfilter können auf verschiedene Arten realisiert werden. Beispielsweise kann sie in einer Gitterform (engl. Lattice) erfolgen oder als eine T-Schaltung. Der passive T-Allpass wurde unter anderem bei Festnetzanschlüssen zur Kompensation von Phasenverzerrungen zwischen Vermittlungsstelle und Endteilnehmeranschluss eingesetzt.
Passive analoge Allpässe Zeitdiskrete Implementierung
Die diskrete Übertragungsfunktion H(z) für einen Allpassfilter 1. Ordnung mit einer komplex konjugierten Pol-Nullstelle bei a weist folgende Form auf:
Literatur
- T. Deliyannis, Yichuang Sun, J. K. Fidler: Continuous-Time Active Filter Design. 1. Auflage. CRC Press, 1999, ISBN 0-84932573-0.
- Karl-Dirk Kammeyer, Kristian Kroschel: Digitale Signalverarbeitung. 6. Auflage. Teubner, 2006, ISBN 3-8351-0072-6.
Weblinks
Wikimedia Foundation.