- Heisenbergmodell
-
Dieser Artikel wurde aufgrund von inhaltlichen Mängeln auf der Qualitätssicherungsseite des Portals Physik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Physik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die nicht signifikant verbessert werden können. Hilf mit, die inhaltlichen Mängel dieses Artikels zu beseitigen, und beteilige dich an der Diskussion.
Das Heisenberg-Modell in der quantenmechanischen Formulierung ist ein mathematisches Modell zur Beschreibung von Ferromagnetismus (sowie Anti-Ferromagnetismus & Ferrimagnetismus) in Festkörpern. 1929 haben Werner Heisenberg[1] und Paul Dirac [2] erkannt, dass Ferromagnetismus in einem Festkörper durch einen effektiven Hamiltonoperator beschrieben werden kann, der lediglich aus wechselwirkenden lokalisierten Elektronenspins auf einem Gitter (dem Kristallgitter) aufgebaut ist. Die Wechselwirkung ist dabei (zunächst) reduziert auf benachbarte Spins (nächste Nachbarwechselwirkung):Die Austauschwechselwirkung zwischen den lokalisierten Spins wird durch die Coulomb-Abstoßung und das Pauli-Prinzip verursacht und wird mittels der Kopplungskonstante J ausgedrückt. Das Modell ist geeignet um Ferromagnetismus in Isolatoren qualitativ zu beschreiben, versagt aber bei den meisten Metallen (hier ist das Hubbard-Modell besser geeignet). Das Heisenberg-Modell ist ein Spezialfall des n-Vektor-Modells mit n = 3. Das Modell kann in einer Dimension exakt gelößt werden. In zwei und drei Dimensionen gibt es lediglich genäherte Lösungen z. B. mittels Quanten-Monte-Carlo-Methoden. Im Gegensatz zum klassischen Heisenberg-Modell werden die Spins mittels Spinoperatoren ausgedrückt und gehorchen den Regeln der Quantenmechanik.
Inhaltsverzeichnis
Erläuterungen zum Modell
Der Ferromagnetismus von Isolatoren wird bewirkt von lokalisierten magnetischen Momenten, die einer unvollständig gefüllten Elektronenschale (3d-, 4d, 4f oder 5f) zuzuschreiben sind. Diesen lokalisierten magnetischen Momenten
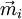 ist ein Drehimpuls
ist ein Drehimpuls 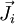 zugeordnet, welcher mit dem jeweiligen Spin
zugeordnet, welcher mit dem jeweiligen Spin 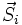 ausgedrückt werden kann:
ausgedrückt werden kann:Der Spinvektor
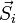 ist gegeben über die Spin-1/2-Operatoren, gJ ist der Landé-Faktor und μB ist das Bohrsches Magneton. Die Austauschwechselwirkung zwischen den magnetischen Momenten kann so mittels der der zugehörigen Spins ausgedrückt werden. Die Austauschwechselwirkung simuliert also die Coulombabstoßung und das Pauliprinzip. Die Kopplungskonstante J zwischen den lokalisierten Spins werden daher auch Austauschintegrale genannt. Man nimmt an, dass die Austauschintegrale nur für benachbarte Spins merklich von null verschieden sind. Insgesamt erhält man so also einen effektiven Hamiltonoperator der darauf ausgelegt ist lediglich den Ferromagnetismus bei Isolatoren zu erklären.
ist gegeben über die Spin-1/2-Operatoren, gJ ist der Landé-Faktor und μB ist das Bohrsches Magneton. Die Austauschwechselwirkung zwischen den magnetischen Momenten kann so mittels der der zugehörigen Spins ausgedrückt werden. Die Austauschwechselwirkung simuliert also die Coulombabstoßung und das Pauliprinzip. Die Kopplungskonstante J zwischen den lokalisierten Spins werden daher auch Austauschintegrale genannt. Man nimmt an, dass die Austauschintegrale nur für benachbarte Spins merklich von null verschieden sind. Insgesamt erhält man so also einen effektiven Hamiltonoperator der darauf ausgelegt ist lediglich den Ferromagnetismus bei Isolatoren zu erklären.Verallgemeinerungen des Modells
Das Heisenberg-Modell kann verallgemeinert werden, indem man die Kopplungskonstante richtungsabhängig macht.
Ein Spezialfall des verallgemeinerten Heisenberg-Modells ist das XXZ-Modell, welches erzeugt wird durch die Setzung von J = Jx = Jy und Jz = Δ:
Das Heisenberg-Modell und seine Spezialfälle werden oft im Zusammenhang mit einem angelegten Magnetfeld h = gJμBB0 in z-Richtung betrachtet. Der Hamiltonian lautet dann:
Eine weitere Verallgemeinerung beinhaltet die Einbeziehung von Kopplungen nicht nur zwischen nächsten Nachbarn und einer inhomogenen Kopplungskonstante
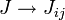 :
:
Die Zusammenhänge zum Ising-Modell und zum XY-Modell sind am Besten im N-Vektor-Modell zu sehen.Modell im k-Raum
Zur Analyse des Modells und zur Betrachtung der Anregungen ist es sinnvoll, dass Modell im k-Raum zu betrachten. Die Transformation (diskrete Fouriertransformation) für die Spinoperatoren a = {x,y,z, + , − } lautet:
Das verallgemeinerte Heisenbergmodells im Magnetfeld ohne Richtungsabhängigkeit
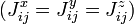 mit Jij = Jji und Jii = 0 läßt sich dann schreiben als:
mit Jij = Jji und Jii = 0 läßt sich dann schreiben als:wobei auch die Austauschintegrale wellenzahlabhängig sind:
Grundzustand
In diesem Abschnitt wird der Grundzustand des verallgemeinerte Heisenberg-Modells im Magnetfeld ohne Richtungsabhängigkeit betrachtet. Der Grundzustand ist der Eigenzustand des Systems mit geringster Energie. Dieser ist stark abhängig von Vorzeichen der Kopplungskonstante J.
Unter eine Drehung aller Spinvektoren ändert sich das Heisenberg-Modell nicht, es ist also invariant unter einer Rotation. Für J > 0 ist es für die Spins energetisch günstiger sich in dieselbe Richtung auszurichten und man spricht von einem ferromagnetischer Grundzustand. Aufgrund der Rotationsinvarianz ist keine Richtung ausgezeichnet, daher wird die Ausrichtung in z-Richtung angenommen. Die Richtung im Festkörper wird durch Anisotropien oder durch ein schwaches angelegtes Magnetfeld bestimmt. Im ferromagnetischen Grundzustand
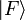 sind alle Spins ausgerichtet in eine Richtung. Spezialisiert man noch
sind alle Spins ausgerichtet in eine Richtung. Spezialisiert man nochJ0 = ∑ Jij = ∑ Jij i j dann kann die Grundzustandsenergie angeben werden als:
Dabei wurde der Eigenwert des
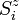 -Operators als
-Operators als 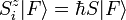 benutzt. Für das Spin-1/2-Heisenberg-Modell ist S = 1 / 2.
benutzt. Für das Spin-1/2-Heisenberg-Modell ist S = 1 / 2.Für J < 0 ist es energetisch günstiger, wenn benachbarte Spins in unterschiedliche Richtungen zeigen. Der Grundzustand ist daher stark vom unterliegenden Kristallgitter abhängig. Dieser kann dann antiferromagnetisch oder ferrimagnetisch sein. Für spezielle Kristallgitter kann es auch zu magnetischer Frustration kommen.
Magnonen und Spinwellen
In diesem Abschnitt werden die Anregungen aus dem ferromagnetischen Grundzustand des verallgemeinerte Heisenberg-Modells im Magnetfeld ohne Richtungsabhängigkeit betrachtet. Die Anregungszustände werden dem Quasiteilchen Magnon zugeordnet. Es handelt sich dabei um kollektive Anregungen des gesamten Kristallgitters und diese werden demnach auch als Spinwellen bezeichnet.
Die Eigenzustände des
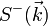 -Operators sind ebenfalls Eigenzustände des Hamiltonians, da
-Operators sind ebenfalls Eigenzustände des Hamiltonians, da 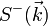 und H kommutieren:
und H kommutieren:Die einmalige Anwendung des
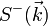 -Operators auf den ferromagnetischen Grundzustand gibt also einen angeregten Eigenzustand des Heisenberg-Modells und wird (normierter) Ein-Magnonenzustand genannt:
-Operators auf den ferromagnetischen Grundzustand gibt also einen angeregten Eigenzustand des Heisenberg-Modells und wird (normierter) Ein-Magnonenzustand genannt:die zugehörige Energie des Zustands ist gegeben als:
die Anregungsenergie
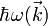 wird dem Quasiteilchen Magnon zugeschrieben. Betrachtet man den Erwartungswert des
wird dem Quasiteilchen Magnon zugeschrieben. Betrachtet man den Erwartungswert des 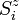 -Operators auf diesen Zustand so erhält man:
-Operators auf diesen Zustand so erhält man:Dabei ist die linke Seite der Gleichung nicht mehr vom Platz i abhängig. Anschaulich bedeutet dies, dass die Anregung aus dem Grundzustand (Ein-Magnonenzustand) nicht durch das einfache Umklappen eines Spins auf einem Gitterplatz erzeugt wird, sondern dass der Ein-Magnonenzustand über das Gitter gleichmäßig verteilt ist. Daher wird der Zustand
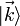 als kollektive Anregung angesehen und als Spinwelle bezeichnet.
als kollektive Anregung angesehen und als Spinwelle bezeichnet.1D-Heisenberg-Modell
Im eindimensionalen Heisenberg-Modell sind die Spins aufgereiht auf einer Kette. Bei periodischen Randbedingungen ist die Kette zu einem Ring geschlossen. Die Eigenzustände und Eigenenergien für das eindimensionale Heisenberg-Modell wurden 1931 von Hans Bethe[3] mit dem Bethe-Ansatz exakt bestimmt.
Eigenvektoren und Eigenzustände
Da der
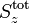 -Operator mit dem Hamiltooperator kommutiert zerfällt der gesamte Hilbertraum in verschiedene Unterräume, die einzeln diagonalisiert werden können.
-Operator mit dem Hamiltooperator kommutiert zerfällt der gesamte Hilbertraum in verschiedene Unterräume, die einzeln diagonalisiert werden können.Die verschieden Unterräume können durch ihre
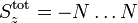 Quantenzahlen beschrieben werden. Das heißt, dass die Eigenvektoren Superpositionen aus Basiszuständen mit derselben
Quantenzahlen beschrieben werden. Das heißt, dass die Eigenvektoren Superpositionen aus Basiszuständen mit derselben 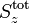 Quantenzahl sind. Im Bethe-Ansatz werden diese Zustände mittels der umgeklappten Zustände vom ferromagnetischen Grundzustand klassifiziert. Zum Beispiel wird der Zustand mit zwei umgeklappten Spins (also
Quantenzahl sind. Im Bethe-Ansatz werden diese Zustände mittels der umgeklappten Zustände vom ferromagnetischen Grundzustand klassifiziert. Zum Beispiel wird der Zustand mit zwei umgeklappten Spins (also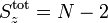 ) an den Gitterplätzen n1 und n2 angegeben als:
) an den Gitterplätzen n1 und n2 angegeben als:Die Eigenvektoren in einem Unterraum mit einer Sz Quantenzahl Sz = N − r sind Superpositionen aus allen möglichen Zuständen
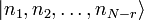
die Koeffizienten sind ebene Wellen und durch den Bethe-Ansatz gegeben.
Die Parameter können über die Bethe-Ansatz Gleichungen bestimmt werden
Die Eigenvektoren sind gegeben mit allen Kombinationen der Bethe Quantenzahlen
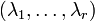 , die die Bethe Ansatz Gleichungen erfüllen. Eine Klassifikation der Eigenvektoren ist also über die Bethe Quantenzahlen möglich. Die Bestimmung aller Eigenvektoren ist allerdings nicht trivial. Diezugehörige Energie des Zustands ist gegeben als:
, die die Bethe Ansatz Gleichungen erfüllen. Eine Klassifikation der Eigenvektoren ist also über die Bethe Quantenzahlen möglich. Die Bestimmung aller Eigenvektoren ist allerdings nicht trivial. Diezugehörige Energie des Zustands ist gegeben als:Jordan-Wigner-Transformation
Das 1D-Heisenberg-Modell kann bei periodischen Randbedingungen mittels einer Jordan-Wigner-Transformation auf spinlose Fermionen auf einer Kette mit lediglich nächster Nachbarwechselwirkung abgebildet werden. Der Hamiltonian HHeis des 1D-Heisenberg Modells kann demnach geschrieben werden als:
Die
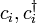 sind Erzeugungs- und Vernichtungsoperatoren für spinlose Fermionen.
sind Erzeugungs- und Vernichtungsoperatoren für spinlose Fermionen.Literatur
- Wolfgang Nolting Grundkurs Theoretische Physik 7 - Viel-Teilchen-Theorie, Springer Verlag
Quellen
- ↑ W. Heisenberg, Z. Phys. 38, 441 (1926)
- ↑ P. Dirac, Proc. Roy. Soc. London 112A, 661 (1926)
- ↑ H. Bethe, Zur Theorie der Metalle. I. Eigenwerte und Eigenfunktionen der linearen Atomkette. (On the theory of metals. I. Eigenvalues and eigenfunctions of the linear atom chain), Zeitschrift für Physik A, Vol. 71, pp. 205-226 (1931). SpringerLink.
Wikimedia Foundation.


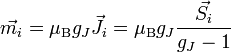
![\begin{align}
H_{\text{Heis}}&amp;amp;=-J\sum_{&amp;lt;i,j&amp;gt;}\vec{S_i}\vec{S_j} \qquad \text{mit } i,j\; \mathrm{n\ddot achste}\text{ Nachbarn}\\
&amp;amp;=-J\sum_{&amp;lt;i,j&amp;gt;}\left(S^x_iS^x_j+S^y_iS^y_j+S^z_iS^z_j\right) \\
&amp;amp;=-J\sum_{&amp;lt;i,j&amp;gt;}\left[\frac{1}{2}\left(S^+_iS^-_j+S^-_iS^+_j\right)+S^z_iS^z_j\right]
\end{align}](/pictures/dewiki/99/c020720a8ecbf73840aaaa450b90fc37.png)
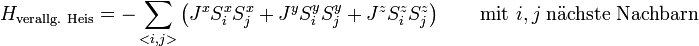
![\begin{align}
H_{\text{XXZ}}&amp;amp;=-\sum_{&amp;lt;i,j&amp;gt;}\left[ J\left( S^x_iS^x_j+S^y_iS^y_j \right)+\Delta S^z_iS^z_j \right] \qquad \text{mit } i,j\; \mathrm{n\ddot achste}\text{ Nachbarn}\\
&amp;amp;=-\sum_{&amp;lt;i,j&amp;gt;}\left[\frac{J}{2}\left(S^+_iS^-_j+S^-_iS^+_j\right)+\Delta S^z_iS^z_j\right]
\end{align}](/pictures/dewiki/98/b9ea6c2c80720187da2a28a2e809624b.png)
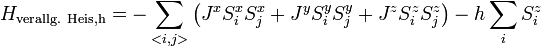
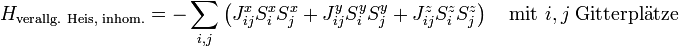
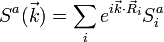
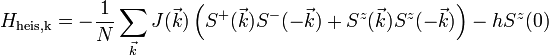
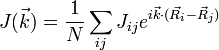
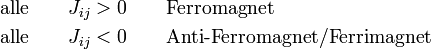
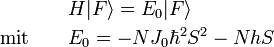
![[H_{\text{heis,k}},S^-(\vec{k})]=0](/pictures/dewiki/100/d5a872b5858cef914f0b94a1a709fc16.png)
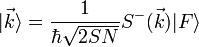
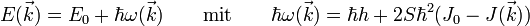
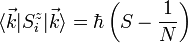
![[S_z^\text{tot},H]=\sum^N_{i=1}[S^z_i,H]=0](/pictures/dewiki/55/7aed48c15cda18ba92f23b289ec80691.png)
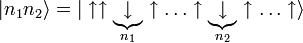

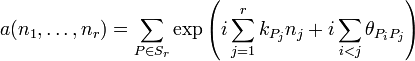
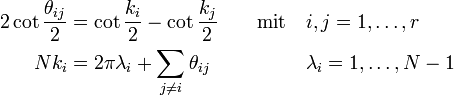
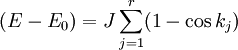
![\begin{align}
H_{\text{Heis}}&amp;amp;=-J\sum^N_{n=1}\vec{S}_n\cdot \vec{S}_{n+1}=-J\sum^N_{n=1}\left[\frac{1}{2}(S_n^+S^-_{n+1} + S_n^-S^+_{n+1})+S^z_nS^z_{n+1} \right] \\
&amp;amp;= -J\sum^N_{i=1}\left[ \left(c^\dagger_i c_{i+1} +\text{h.c}\right) + \left( c^\dagger_i c_i - \frac{1}{2}\right)\left(c^\dagger_{i+1} c_{i+1} - \frac{1}{2}\right) \right]\\
&amp;amp;= H_0 + H_J
\end{align}](/pictures/dewiki/99/cae990894165da32fb944ab7211a5c80.png)