- Katastrophentheorie (Mathematik)
-
Die mathematische Katastrophentheorie beschäftigt sich mit unstetigen, sprunghaften Veränderungen von bestimmten dynamischen Systemen. Diese können, auch wenn sie unter bestimmten Voraussetzungen einen stabilen Zustand anstreben, bei Änderungen der Parameter sprunghafte, nichtstetige, diskontinuierliche Änderungen der Lösung erfahren. Die Katastrophentheorie untersucht das Verzweigungs-Verhalten dieser Lösungen (Bifurkationen) bei Variation der Parameter und ist damit eine wichtige Grundlage zur mathematischen Behandlung der Chaostheorie. Manchmal wird in der Mathematik lieber von Theorie der Singularitäten differenzierbarer Abbildungen gesprochen, und der reißerische Name Katastrophentheorie vermieden.
Die Katastrophentheorie fußt grundlegend auf der Differentialgeometrie (bzw. Differentialtopologie). Entwickelt wurde sie Ende der 1960er Jahre von René Thom, Wladimir Arnold und anderen. Sie findet Anwendung unter anderem in der modernen Physik und Ökonomie, aber auch in der Linguistik und der Psychologie und war deshalb auf diesen Gebieten in den 1970er Jahren als eine unmittelbar anwendbare qualitative mathematische Methode beliebt. Besonders aktiv war dabei der englische Mathematiker Erik Christopher Zeeman, der die Theorie von der Schiffsstabilität bis zur Evolutionstheorie einsetzte. Thom selbst suchte, wie der Titel seines Buches von 1972 zeigt, vor allem Anwendungen in der Biologie (speziell der Embryo-Entwicklung, Morphogenese).
Inhaltsverzeichnis
Elementare Katastrophen
Die Katastrophentheorie analysiert entartete kritische Punkte von Potentialfunktionen. Das sind Punkte, bei denen neben allen ersten Ableitungen auch einige der höheren Ableitungen Null sind. Die Punkte bilden den Keim (germ) der Katastrophen-Geometrien. Die Entartung kann durch Entwicklung der Potentialfunktion in einer Taylorreihe und kleine Störung des Parameters „entfaltet“ werden.
Lassen sich die kritischen Punkte durch kleine Störungen nicht beseitigen, nennt man sie strukturell stabil. Ihre geometrische Struktur lässt sich bei drei oder weniger Variablen der Potentialfunktion und fünf oder weniger Parametern dieser Funktion durch nur sieben Typen von (Bifurkations-)Geometrien klassifizieren. Sie entsprechen den Normalformen, auf die die Taylorentwicklung um Katastrophen-Keime mit Hilfe von Diffeomorphismen (differenzierbaren Abbildungen) zurückgeführt werden kann.
Potentialfunktionen einer Variable
In der Praxis sind die Faltungsbifurkationen und die Spitzen-Katastrophe (Cusp-Geometrie) die bei weitem wichtigsten Fälle der Katastrophentheorie und treten in zahlreichen Fällen auf. Die restlichen Katastrophen sind dagegen sehr speziell und werden hier nur der Vollständigkeit halber aufgeführt.
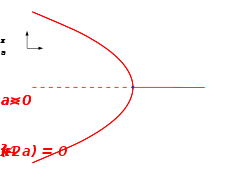
Faltungs-Katastrophe (fold)
Bei negativen Werten von a hat die Potentialfunktion ein stabiles und ein instabiles Extremum. Nimmt der Parameter a langsam zu, kann das System dem stabilen Minimum folgen. Bei a = 0 treffen sich die stabilen und instabilen Extrema und heben sich auf (Bifurkationspunkt). Für a>0 gibt es keine stabile Lösung mehr. Ein physikalisches System würde bei a = 0 seine für negative a vorhandene Stabilität plötzlich verlieren und sein Verhalten umkippen.
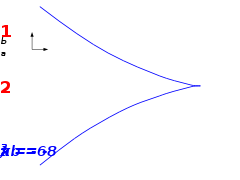
Spitzen-Katastrophe (Cusp)
Die Cusp-Katastrophe tritt ziemlich häufig auf bei Betrachtung des Verhaltens einer Faltungs-Katastrophe, wenn ein zweiter Parameter b dem Parameterraum hinzugefügt wird. Ändert man nun die Parameter, gibt es eine Kurve (in der Abbildung blau) von Punkten im Parameterraum (a,b), bei deren Überschreiten die Stabilität verlorengeht. Statt einem Extremum gibt es nun zwei zu denen das System springen kann. Ändert man periodisch b, kann man so auch im Ortsraum ein „Hin- und Herspringen“ erzeugen. Das ist allerdings nur für den Bereich a<0 möglich, je mehr sich a Null nähert, desto kleiner werden die Hysterese-Kurven und verschwinden bei a = 0 schließlich ganz.
Hält man umgekehrt b konstant und variiert a beobachtet man im symmetrischen Fall b = 0 eine Stimmgabel-Bifurkation (Pitchfork-Bifurcation): nimmt a ab, spaltet sich eine stabile Lösung plötzlich in zwei stabile und eine instabile Lösung auf, wenn das System den Cusp Punkt a=0, b=0 zu negativen Werten von a passiert. Das ist ein Beispiel für spontanen Symmetriebruch. Weiter weg vom Cusp-Punkt fehlt dieser plötzliche Wechsel in der Struktur der Lösung und es taucht einzig eine zweite mögliche Lösung auf.
Ein bekanntes Beispiel modelliert mit dem Cusp das Verhalten eines gestressten Hundes zwischen Unterwürfigkeit und Angriffslust. Bei mäßigem Stress (a>0) zeigt der Hund je nach Provokation (Parameter b) ein stetiges Übergangsverhalten zwischen beiden Verhaltensweisen. Bei höherem Stress (Region a < 0) bleibt der Hund auch bei abgeschwächter Provokation in eingeschüchtertem Zustand, um dann plötzlich bei Erreichen des Faltungspunktes in aggressives Verhalten umzukippen, was er auch bei Reduzierung des Provokationsparameters beibehält.
Schwalbenschwanz (Swallowtail) Katastrophe
Hier ist der Raum der Kontrollparameter dreidimensional. Die Bifurkationsmenge besteht aus drei Flächen von Faltungskatastrophen, die sich in zwei Cusp-Bifurkationen treffen. Diese wiederum treffen sich in einem einzigen Schwalbenschwanz-Bifurkationspunkt.
Gehen die Parameter durch die Flächen der Faltungs-Bifurkationen, verschwindet ein Minimum und ein Maximum der Potentialfunktion. An den Cusp-Bifurkationen werden zwei Minima und ein Maximum durch ein Minimum ersetzt, hinter ihnen verschwindet die Faltungs-Bifurkation. Im Schwalbenschwanz-Punkt treffen sich zwei Minima und zwei Maxima an einem einzigen Punkt x. Für Werte a>0, jenseits des Schwalbenschwanzes, gibt es abhängig von den Parameterwerten b und c entweder ein Maximum-Minimum-Paar oder überhaupt keines. Zwei der Flächen der Faltungs-Bifurkationen und die beiden Kurven der Cusp-Bifurkationen verschwinden im Schwalbenschwanz-Punkt und nur eine einzige Fläche von Faltungs-Bifurkationen bleibt. Salvador Dalí's letztes Gemälde Der Schwalbenschwanz basierte auf dieser Katastrophe.
Schmetterlings-Katastrophe (butterfly)
Abhängig von den Parametern kann die Potentialfunktion 3, 2 oder 1 lokales Minimum haben. Die verschiedenen Bereiche werden im Parameterraum durch Faltungsbifurkationen getrennt. Am Schmetterlings-Punkt treffen sich die verschiedenen 3-Flächen von Faltungsbifurkationen, 2-Flächen von Cusp-Bifurkationen und Kurven von Schmetterlings-Bifurkationen und verschwinden, um nur eine einzige Cusp-Struktur für a>0 übrigzulassen.
Potentialfunktionen in zwei Variablen
Umbilic catastrophes ("Nabel") sind Beispiele für Ko-Rang 2 Katastrophen. Sie tauchen z.B. in der Optik in den Brennpunktflächen von an Flächen in drei Dimensionen reflektiertem Licht auf und sind eng mit der Geometrie fast-sphärischer Flächen verbunden. Nach Thom modelliert die Hyperbolic umbilic-Katastrophe das Brechen einer Welle und die elliptic umbilic die Entstehung Haar-ähnlicher Strukturen.
Hyperbolic umbilic-Katastrophe
Elliptic umbilic-Katastrophe
Parabolic umbilic-Katastrophe
Arnold's Notation
Wladimir Arnold gab den Katastrophen die ADE-Klassifikation, die auf tiefliegenden Verbindungen zu Liegruppen und -algebren und ihren Dynkin-Diagrammen beruht.
- A0 - ein nicht-singulärer Punkt, V = x.
- A1 - ein lokales Extremum, entweder ein stabiles Minimum oder ein instabiles Maximum
 .
. - A2 - die Faltung, fold
- A3 - die Spitze, cusp
- A4 - der Schwalbenschwanz, swallowtail
- A5 - der Schmetterling, butterfly
- Ak - eine unendliche Folge von Formen in einer Variabler

- D4- - der elliptical umbilic
- D4+ - der hyperbolic umbilic
- D5 - der parabolic umbilic
- Dk - eine unendliche Folge weiterer umbilic Formen
- E6 - der symbolische umbilic V = x3 + y4 + axy2 + bxy + cx + dy
- E7
- E8
Auch den restlichen einfachen Liegruppen entsprechen Objekte in der Theorie der Singularitäten (in ADE steht A für die den speziellen unitären Gruppen entsprechenden Diagramme, D für die der orthogonalen Gruppe entsprechenden, E für spezielle einfache Liegruppen).
Literatur
- Wladimir Arnold: Catastrophe theory. Springer 1998.
- Robert Gilmore: Catastrophe Theory for Scientists and Engineers. Dover, New York 1993.
- Hermann Haken: Synergetik. Springer 1982.
- Tim Poston, Ian Stewart: Catastrophe Theory and Its Applications. Dover, New York 1998, ISBN 0-486-69271-X.
- René Thom: Structural Stability and Morphogenesis: An Outline of a General Theory of Models. Addison-Wesley, Reading, MA 1989, ISBN 0-201-09419-3.
- J. Thompson: Instabilities and Catastrophes in Science and Engineering. Wiley, New York 1982.
- Monte Davis, Alexander Woodcock: Catastrophe Theory. Dutton, New York 1978, Pelican 1980.
- E. C. Zeeman: Catastrophe Theory-Selected Papers 1972–1977. Addison-Wesley, Reading, MA 1977.
Weblinks
- Erklärung im Lexikon der Komplexitätstheorie, englisch
- Erklärung von Dujardin, englisch
- Vorlesungen von E.C.Zeeman, u.a. Katastrophentheorie, englisch
- Michor Elementary catastrophe theory, pdf Datei
Dieser Artikel beruht auf einer Übersetzung des englischsprachigen Artikels in der Version vom 3. April 2007.
Wikimedia Foundation.