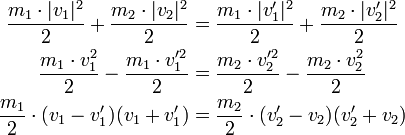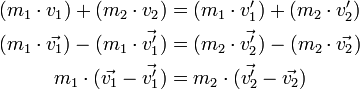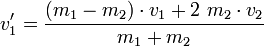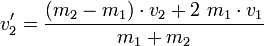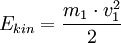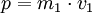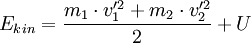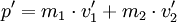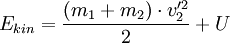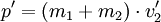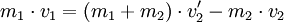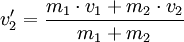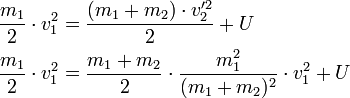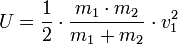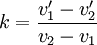- Anelastischer Stoß
-
 Das Kugelstoßpendel veranschaulicht den elastischen Stoß
Das Kugelstoßpendel veranschaulicht den elastischen StoßEin Stoß in der Physik ist eine sehr kurze Wechselwirkung zwischen zwei Teilchen, Körpern oder eine Kombination daraus. Durch den Stoß ändern sich im Allgemeinen Geschwindigkeiten, Impulse und Energien der Stoßpartner.
Man unterscheidet zwischen einem elastischen Stoß und einem plastischen Stoß (manchmal auch inelastisch oder unelastisch, selten auch anelastisch genannt). Beim elastischen Stoß wird kinetische Energie von Körper zu Körper weitergegeben, bleibt aber insgesamt als kinetische Energie erhalten. Beim inelastischen Stoß wird dagegen ein Teil der kinetischen Energie in innere Energie umgewandelt.
Die im folgenden aufgeführten Stoßgesetze zur mathematischen Beschreibung wurden in der Zeit zwischen 1651 und 1655 von Christiaan Huygens aufgestellt.
Inhaltsverzeichnis
Allgemeine Bezeichnungen und Klassifizierung von Stoßprozessen
Die gemeinsame Tangentialebene an die beiden Körper durch deren Berührpunkt liefert die Berührebene, die Normalgerade darauf durch den Berührpunkt die Stoßlinie. Die Massen der beiden Körper seien m1 und m2, ihre Anfangsgeschwindigkeiten
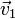 und
und 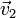 , die Ausgangsgeschwindigkeiten
, die Ausgangsgeschwindigkeiten 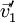 und
und 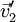 . Die gemeinsame Geschwindigkeit zum Zeitpunkt der Berührung sei
. Die gemeinsame Geschwindigkeit zum Zeitpunkt der Berührung sei 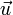 . Bei einem geraden Stoß liegen beide Körperschwerpunkte auf der Stoßlinie, beim schiefen Stoß ist dies nicht der Fall. Verlaufen die Vektoren der Ausgangsgeschwindigkeiten parallel zur Stoßlinie, so spricht man von einem zentralen Stoß, andernfalls von einem exzentrischen Stoß. Nehmen die Körper nach dem Stoß ihre ursprüngliche Form wieder an, so handelt es sich um einen elastischen Stoß, bei welchem keine mechanische Energie in Wärme umgewandelt wird, bleibt die Verformung vollständig wird dies als plastischer Stoß bezeichnet, alle Zwischenstufen nennt man realer Stoß.
. Bei einem geraden Stoß liegen beide Körperschwerpunkte auf der Stoßlinie, beim schiefen Stoß ist dies nicht der Fall. Verlaufen die Vektoren der Ausgangsgeschwindigkeiten parallel zur Stoßlinie, so spricht man von einem zentralen Stoß, andernfalls von einem exzentrischen Stoß. Nehmen die Körper nach dem Stoß ihre ursprüngliche Form wieder an, so handelt es sich um einen elastischen Stoß, bei welchem keine mechanische Energie in Wärme umgewandelt wird, bleibt die Verformung vollständig wird dies als plastischer Stoß bezeichnet, alle Zwischenstufen nennt man realer Stoß.Zentraler Stoß
Im folgenden wird nur der Fall des zentralen Stoßes betrachtet. Wird hierbei freie Beweglichkeit der Stoßpartner vorausgesetzt, so bleiben die Geschwindigkeitskomponenten beider Stoßpartner normal zur Stoßlinie unverändert:
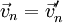 , da die Stoßkräfte nur entlang der Stoßlinie wirken können. Da die Schwerpunkte auf der Stoßlinie liegen, erfahren die Körper nach dem Stoß keine Rotationsbewegung. Im folgenden bezeichnen darum v1 und v2 die (skalaren) Geschwindigkeitskomponenten parallel zur Stoßlinie.
, da die Stoßkräfte nur entlang der Stoßlinie wirken können. Da die Schwerpunkte auf der Stoßlinie liegen, erfahren die Körper nach dem Stoß keine Rotationsbewegung. Im folgenden bezeichnen darum v1 und v2 die (skalaren) Geschwindigkeitskomponenten parallel zur Stoßlinie.Ideal elastischer Stoß
Zwei Körper stoßen aufeinander, ohne dass dabei Energie in innere Energie, beispielsweise Wärme oder Deformation, umgewandelt wird. Nach dem Energieerhaltungssatz ist also die Summe der Bewegungsenergien (kinetische Energien) vor dem Stoß gleich der Summe der kinetischen Energien (Bewegungsenergien) nach dem Stoß. Dasselbe gilt nach dem Impulserhaltungssatz auch für die vektorielle Summe der Impulse.
Der ideale elastische Stoß bei makroskopischen Objekten ist ein physikalisches Modell. Aufgrund von Reibung und weiterer Faktoren geht dem System kinetische Energie verloren. Sehr nahe am Modell sind beispielsweise Billard-Kugeln oder ein Gummiball.
Beim Stoß von Atomen und Elementarteilchen gibt es auf Grund der Quantenmechanik eine Mindestenergie, die für eine Anregung eines Atoms oder Teilchens oder die Erzeugung und Umwandlung von Teilchen in der Elementarteilchenphysik benötigt wird. Wird diese Energie nicht erreicht, kommt es zum ideal elastischen Stoß.
Nach Energieerhaltungssatz muss die Summe der kinetischen Energie vor und nach dem Stoß gleich hoch sein:
Der Impulserhaltungssatz über den Geschwindigkeitsvektoren lautet:
Beim Impuls ist darauf zu achten, die Richtung nicht zu vernachlässigen, da die Betragsaddition in n-dimensionalen Räumen für n > 1 zu große Werte liefert. Beim Quadrat der Vektoren im Energieerhaltungssatz handelt es sich um Skalare. Es ist darauf zu achten, dass die folgende Berechnung nur für die Geschwindigkeiten in Stoßrichtung gelten (tangential), nicht aber für die, die orthogonal dazu liegen.
Im Eindimensionalen reichen die beiden Gleichungen aus, um die zwei Unbekannten v1' und v2' zu berechnen:
Wie man leicht sieht, ist für m1 = m2 die Lösung der Gleichung:- v1' = v2
- v2' = v1
Im Zwei- und Mehrdimensionalen müssen die Bewegungen anhand des Aufprallwinkels zerlegt werden.Plastischer Stoß
Beim unelastischen Stoß wird ein Teil der kinetischen Energie in innere Energie (U) umgewandelt. Wenn diese – was in der Regel der Fall ist – zu einer bleibenden Deformation oder Erwärmung der beteiligten Körper führt, nennt man diesen Stoß auch plastisch.
Wiederum gelten die beiden Erhaltungssätze:
- vor dem Stoß:
- nach dem Stoß:
Beim vollkommen unelastischen Stoß wird der maximal mögliche Anteil der kinetischen Energie in innere Energie umgewandelt, dabei 'kleben' die beiden Massen nach dem Stoß aneinander und fliegen mit derselben Geschwindigkeit, im Folgenden v2' genannt, weiter. Ein Beispiel sind zwei Plastilinkugeln, die nach dem Stoß aneinander haften.
- nach dem Stoß:
Aus dem Impulserhaltungssatz kann man folgendes ableiten:
Aus dem Energieerhaltungssatz lässt sich die innere Energie U berechnen:
Realer Stoß
Ein realer Stoß zwischen 2 Massen stellt immer eine Mischform aus ideal elastischem und ideal plastischem Stoß dar. Diese Mischform wird dargestellt durch die Stoßzahl k.
- k = 0: vollkommen plastischer Stoß
- k = 1: vollkommen elastischer Stoß
Betrachtet man als System nur einen der Körper, so herrscht keine Impulserhaltung, sondern das System ändert seinen Zustand. Dann nennt man die Differenz
- p' − p = Δp = I den Kraftstoß
Er stellt den Antrieb des Körpers dar, der seine Bewegungsgeschwindigkeit und/oder -richtung ändert.
Superelastischer Stoß
Beim superelastischen Stoß geht innere Energie von mindestens einem der Stoßpartner in kinetische Energie über. Die kinetische Energie ist nach diesem Stoß größer als vor dem Stoß. Die mathematische Behandlung erfolgt wie beim allgemeinen inelastischen Stoß, nur ist U < 0.
Reaktiver Stoß
Beim reaktiven Stoß kommt es zu Reaktionen, wie z. B. chemische Reaktionen, oder zur Erzeugung neuer Teilchen durch Stöße hochenergetischer Teilchen in der Elementarteilchenphysik. Dabei muss berücksichtigt werden, dass vor und nach dem Stoß unterschiedliche Teilchen zu Energie und Impuls beitragen. Es ändern sich also neben der Geschwindigkeit auch die Massen und unter Umständen die Anzahl der Teilchen.
Eine Art des reaktiven Stoßes ist z. B. der Ladungsaustausch, ein atomphysikalischer Prozess, bei dem während eines Stoßes zwischen Atomen, Molekülen oder Ionen ein oder mehrere Elektronen ausgetauscht werden. Mit großer Wahrscheinlichkeit werden dabei die Elektronen auf den Stoßpartner mit der positiveren Ladung übergehen. So können z. B. im Sonnenwind enthaltene positive Ionen (siehe auch hochgeladenes Ion) beim Durchgang durch die einen Kometen umgebende dünne Gasatmosphäre Elektronen einfangen und dabei Strahlung, u. a. im Röntgenbereich, emittieren.
Streuung
In der Teilchenphysik, Atomphysik oder wenn Photonen beteiligt sind, spricht man auch von Streuung. Auch hier bedeutet inelastische Streuung (inelastischer Stoß), dass die kinetische Energie nicht als solche erhalten bleibt, sondern teilweise z. B. in Anregungsenergie verwandelt oder zum Aufbrechen von Bindungen verwendet wird. Wenn ein Photon an einer inelastischen Streuung beteiligt sind, ändert sich im Allgemeinen seine Wellenlänge. Näheres siehe Streuung und Streutheorie.
Siehe auch
- Stoßwelle (Schockwelle) – eine energiereiche Druckwelle
- Verdichtungsstoß - Stoßwelle in überschall-schneller Strömung
Literatur
- Christiaan Huygens, Felix Hausdorff: Christiaan Huygens' nachgelassene Abhandlungen: Über die Bewegung der Körper durch den Stoss : Über die Centrifugalkraft / Hrsg. von Felix Hausdorff. Akademische Verlagsgesellschaft, Leipzig, um 1921
Weblinks
- Der elastische Stoß in drei Dimensionen einschließlich Herleitung unter Benutzung der Impuls- und Energieerhaltung
- [1] Dissertation von Dennis Bodewits zum Thema kometarer Röntgenemission.
Wikimedia Foundation.