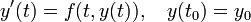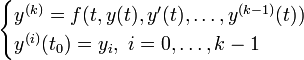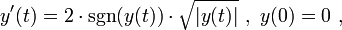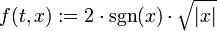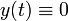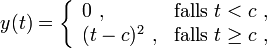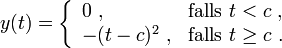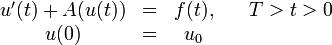- Anfangswertaufgabe
-
Als Anfangswertproblem (AWP) (manchmal auch als Anfangswertaufgabe (AWA) oder Cauchy-Problem genannt) bezeichnet man in der Analysis eine wichtige Klasse von Differentialgleichungen, bei denen aus vorgegebenen Anfangsdaten, nämlich dem Anfangswert y0 und einem Zeitpunkt
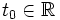 , die Lösung y einer gegebenen Differentialgleichung berechnet werden soll, die zusätzlich y(t0) = y0 genügt. Genauer heißt
, die Lösung y einer gegebenen Differentialgleichung berechnet werden soll, die zusätzlich y(t0) = y0 genügt. Genauer heißtAnfangswertproblem 1. Ordnung.
Inhaltsverzeichnis
Allgemeine Definition
Gegeben seien
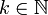 und eine Funktion
und eine Funktion 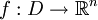 . Der Definitionsbereich D von f sei hierbei eine Teilmenge von
. Der Definitionsbereich D von f sei hierbei eine Teilmenge von 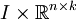 , worin
, worin 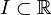 ein Intervall bezeichnet, welches t0 umfasst. Dann heißt
ein Intervall bezeichnet, welches t0 umfasst. Dann heißtein Anfangswertproblem k-ter Ordnung. Jedes Anfangswertproblem k-ter Ordnung lässt sich umschreiben in ein Anfangswertproblem 1. Ordnung.
Ein spezielles Anfangswertproblem ist das Riemann-Problem, bei dem die Anfangsdaten konstant sind bis auf eine Unstetigkeitsstelle.
Anfangswertprobleme treten zum Beispiel in den Naturwissenschaften auf, wenn für natürliche Prozesse ein mathematisches Modell gesucht wird.
Wichtige Sätze, die die Lösbarkeit von Anfangswertproblemen für gewöhnliche Differentialgleichungen betreffen, sind der (lokale) Existenzsatz von Peano und der Existenz- und Eindeutigkeitssatz von Picard-Lindelöf. Ein Hilfsmittel ist die grönwallsche Ungleichung.
Beispiel
Das Anfangswertproblem
welches zu
korrespondiert, hat unendlich viele Lösungen, nämlich neben der trivialen Lösung
auch noch für jedes
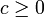 die Lösungen
die Lösungensowie
Damit Anfangswertprobleme eindeutige Lösungen besitzen, sind Zusatzeigenschaften (an f) nachzuweisen. Ein hinreichendes Kriterium hierfür liefert der Satz von Picard-Lindelöf, welches in diesem Beispiel jedoch verletzt ist.
Abstraktes Cauchy-Problem
Seien X ein Banachraum und
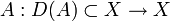 ein linearer oder nichtlinearer Operator. Die Fragestellung, ob bei gegebenem T > 0,
ein linearer oder nichtlinearer Operator. Die Fragestellung, ob bei gegebenem T > 0, 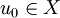 und
und 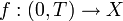 eine differenzierbare Funktion
eine differenzierbare Funktion 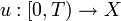 mit
mit 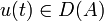 für alle T > t > 0 existiert, die das Anfangswertproblem
für alle T > t > 0 existiert, die das Anfangswertproblemerfüllt, bezeichnet man als abstraktes Cauchy-Problem. Zu ihrer Lösbarkeit benötigt man die Theorie der stark stetigen Halbgruppen bzw. der analytischen Halbgruppen. Zu den verschiedenen Anfangsbedingungen und Operatoren gibt es verschiedene Arten des Lösungsbegriffes, im linearen distributionelle Lösungen, im nichtlinearen die integrale Lösung. Mit klassisch differenzierbaren, beziehungsweise fast überall differenzierbaren Lösungen beschäftigt sich die nachgelagerte Regularitätstheorie.
Numerische Lösung
Zur numerischen Lösung von Anfangswertproblemen werden Einschritt- oder Mehrschrittverfahren eingesetzt. Dabei wird die Differentialgleichung mittels einer Diskretisierung approximiert.
Literatur
- Wolfgang Walter: Gewöhnliche Differentialgleichungen: Eine Einführung, 7. Auflage, Springer, 2000, ISBN 3540676422
- Isao Miyadera, Choong Yun Cho: Nonlinear Semigroups
- Amnon Pazy: Semigroups of Linear Operators and Applications to Partial Differential Equations
Weblinks
- Prof. Gert Lube: Anfangswertaufgaben (Skript, Universität Göttingen)
- Prof. Clemens Brand: Illustrationen zu einem einfachen Anfangswertproblem (Skript, Uni Leoben)
Wikimedia Foundation.