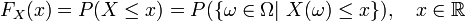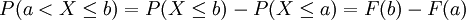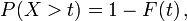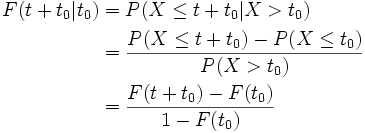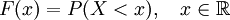- Kumulierte Verteilungsfunktion
-
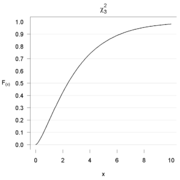
Die (kumulative) Verteilungsfunktion F(x) wird in der Wahrscheinlichkeitstheorie verwendet, um die Wahrscheinlichkeitsverteilung einer reellen Zufallsvariable X zu beschreiben. In der Regel spricht man einfach von einer Verteilungsfunktion. Die explizite Kennzeichnung als kumulativ kann helfen, Verwechslungen mit der Wahrscheinlichkeitsfunktion oder Dichtefunktion zu vermeiden.
Inhaltsverzeichnis
Definition
Auf einem Wahrscheinlichkeitsraum (Ω,Σ,P) wird die Verteilungsfunktion einer reellen Zufallsvariablen :
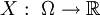 meist als diejenige Funktion
meist als diejenige Funktion 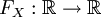 definiert, die angibt, mit welcher Wahrscheinlichkeit die Zufallsvariable einen Wert kleiner oder gleich x annimmt:[1]
definiert, die angibt, mit welcher Wahrscheinlichkeit die Zufallsvariable einen Wert kleiner oder gleich x annimmt:[1]Wenn klar ist, bezüglich welcher Zufallsvariablen die Verteilungsfunktion definiert ist, so wird diese mit F(x) angegeben.
Gelegentlich findet sich auch eine leicht abweichende Definition, siehe den Abschnitt alternative Definition.
Eigenschaften von Verteilungsfunktionen
Jede Verteilungsfunktion
![F:\R\rightarrow [0,1]](/pictures/dewiki/55/7e61075ae165601770e4d571e4600b2d.png) hat folgende Eigenschaften:
hat folgende Eigenschaften:- F ist monoton steigend.
- F ist rechtsseitig stetig.
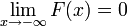 und
und 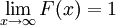 .
.
Rechnen mit Verteilungsfunktionen
Ist von einer Zufallsvariablen die Verteilungsfunktion bekannt, so kann man die Wahrscheinlichkeit berechnen, mit der die Zufallsvariable Werte zwischen zwei reellen Zahlen annimmt:
- Beispiel
Beim Würfeln errechnet sich die Wahrscheinlichkeit eine Zahl zwischen 3 und 5 einschließlich zu würfeln zu
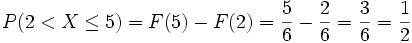 .
.
Überlebenswahrscheinlichkeit
Beschreibt die Verteilungsfunktion F(t) die Wahrscheinlichkeit das Auftreten eines Defektes in einem System zum Zeitpunkt t, dann erhält man die Wahrscheinlichkeit für das einwandfreie Funktionieren (Überleben) über t hinaus
wobei X den Zeitpunkt des Defektes (oder Todes) bezeichnet.
Bezieht man sich nicht auf den Zeitpunkt 0, sondern auf einen späteren Zeitpunkt t0 > 0, dann erhält man die bedingte Überlebenswahrscheinlichkeit
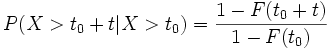 .
.
Mit der Beziehung für die Überlebenswahrscheinlichkeit ergibt sich sofort eine Beziehung für die Restlebensdauer
Weiteres
- Verteilungsfunktionen können zur Definition der Konvergenz in Verteilung verwendet werden und spielen bei der Inversionsmethode eine Rolle.
- Durch die Folge der relativen Summenhäufigkeiten wird die empirische Verteilungsfunktion bestimmt.
- Zu jeder Funktion
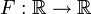 mit den oben genannten Eigenschaften (monoton nicht-fallend, rechtsseitig stetig, Grenzwerteigenschaften) existiert genau eine Verteilung PF über
mit den oben genannten Eigenschaften (monoton nicht-fallend, rechtsseitig stetig, Grenzwerteigenschaften) existiert genau eine Verteilung PF über 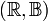 , das F die zu PF gehörige Verteilungsfunktion ist. In der Literatur wird dieser Sachverhalt manchmal Korrespondenzsatz genannt[2].
, das F die zu PF gehörige Verteilungsfunktion ist. In der Literatur wird dieser Sachverhalt manchmal Korrespondenzsatz genannt[2].
Alternative Definition
Gelegentlich wird in der Literatur die Verteilungsfunktion mit echt-kleiner statt mit kleiner-gleich definiert,[3] also
Bei stetigen Wahrscheinlichkeitsverteilungen stimmen beide Definitionen überein; bei diskreten Verteilungen unterscheiden sie sich darin, dass bei der „echt-kleiner“-Definition die Verteilungsfunktion an den Sprungstellen nicht rechtsseitig, sondern linksseitig stetig ist. Beispielsweise ergibt sich für die Binomialverteilung die Verteilungsfunktion bei der „kleiner-gleich“-Definition als
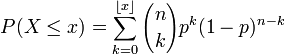 ,
,
bei der „echt-kleiner“-Definition hingegen als
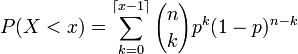 .
.
Im Prinzip sind aber beide Definitionen gleichwertig.
Siehe auch
Einzelnachweise
- ↑ Robert B. Ash: Real Analysis and Probability. Academic Press, New York 1972. ISBN 0-12-065201-3. Definition 5.6.2.
- ↑ Schmitz, N Vorlesungen über Wahrscheinlichkeitstheorie, Teubner, 1996
- ↑ z.B. Marek Fisz: Wahrscheinlichkeitsrechnung und mathematische Statistik. VEB Deutscher Verlag der Wissenschaften, Elfte Auflage, Berlin 1989, Definition 2.2.1, Seite 51.
Wikimedia Foundation.