- LR(k)
-
In der theoretischen Informatik und dem Compilerbau bezeichnet LR(k)-Grammatik eine spezielle kontextfreie Grammatik, welche die Grundlage eines LR(k)-Parsers bildet.
Man nennt eine kontextfreie Grammatik LR(k)-Grammatik, wenn jeder Reduktionsschritt eindeutig durch k Symbole der Eingabe (Lookahead) bestimmt ist. Das bedeutet, die Frage, zu welchem Nichtterminalsymbol mit welcher Regel als nächstes reduziert werden soll, kann eindeutig mit Hilfe der nächsten k Symbole der Eingabe bestimmt werden.
Ein Unterschied der Sprachklasse, die mit LR(k)-Grammatiken beschrieben werden kann, zeigt sich nur für die beiden Fälle k = 0 und k > 0. Die Ausdrucksstärke von kontextfreien Grammatiken wird von LR(1) nicht erreicht. Damit gibt es kontextfreie Grammatiken, die für kein k LR(k)-Grammatiken sind, zum Beispiel die inhärent mehrdeutigen Sprachen. Man nennt die durch LR(k)-Grammatiken definierte Sprachklasse auch deterministisch kontextfreie Sprachen.
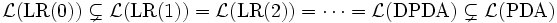 (DPDA = Deterministic Push-Down Automaton, PDA = Push-Down Automaton)
(DPDA = Deterministic Push-Down Automaton, PDA = Push-Down Automaton)Formale Definition LR(k)-Grammatik
Eine kontextfreie Grammatik
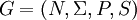 ist
ist 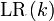 -Grammatik genau dann, wenn für alle Rechtsreduktionen der Form
-Grammatik genau dann, wenn für alle Rechtsreduktionen der Form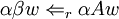
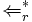
S 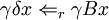
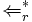
mit
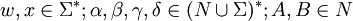 und
und 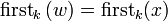 gilt:
gilt:α = γ, A = B sowie β = δ Siehe auch
Weblinks
Wikimedia Foundation.
