- Laplacegleichung
-
Dieser Artikel erläutert die partielle Differentialgleichung; die Berechnung des Drucks in einem kleinen Wassertropfen, der von der Oberflächenspannung hervorgerufen wird, ermöglicht die Young-Laplace-Gleichung.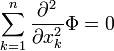 
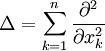
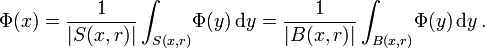
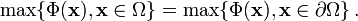
- Burg, Haf, Wille: Höhere Mathematik für Ingenieure 5. Funktionalanalysis und Partielle Differentialgleichungen, 3. Auflage, 2004, Teubner
Die Laplace-Gleichung (nach Pierre-Simon Laplace) ist die partielle Differentialgleichung zweiter Ordnung
für eine Funktion Φ in einem Gebiet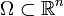 
. Damit ist sie die homogene Poisson-Gleichung, das heißt, die rechte Seite ist null. Die Laplace-Gleichung ist der Prototyp einer elliptischen partiellen Differentialgleichung.
Ist der Rand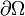 
glatt und gibt man dort stetige Werte von Φ (Dirichlet-Randbedingung) oder stetige Werte der Normalenableitung von Φ (Neumann-Randbedingung) vor, so existiert eine Lösung der Laplace-Gleichung und die Lösung ist (im zweiten Fall bis auf eine Konstante) eindeutig.
heißt Laplace-Operator.
Eine Funktion Φ heißt harmonisch im Gebiet Ω, falls sie dort zweimal stetig differenzierbar ist und die Laplace-Gleichung erfüllt.
Mittelwerteigenschaft und Minimax-Prinzip
Ist Φ im Gebiet Ω harmonisch, so ist ihr Funktionswert Φ(x) an jeder Stelle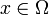 
gleich dem Mittelwert von Φ auf der Oberfläche jeder Kugel B(x,r) um x mit Radius r, sofern die Kugel in Ω liegt,
Hierbei ist S(x,r) die Kugeloberfläche der Kugel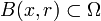 
mit Mittelpunkt 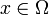und Radius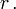 
Weil der Mittelwert zwischen dem Minimum und Maximum liegt, nimmt eine harmonische Funktion, die auf dem Abschluss von Ω stetig ist, ihr Minimum und Maximum auf dem Rand an,
Bedeutung in der Physik
In der Elektrostatik genügt das elektrische Potential im ladungsfreien Raum der Laplace-Gleichung. Sind eine geometrische Leiteranordnung sowie das Potential der Leiter gegeben, so liegen Dirichlet-Randbedingungen vor (sofern die Leiter kein beschränktes Gebiet umschließen, nimmt man als weitere Randbedingung an, dass das Potential im Unendlichen gegen null geht). Dann gibt es genau eine Lösung der Laplace-Gleichung, das elektrostatische Potential. Beispielsweise ist das Potential in einem Faradayschen Käfig konstant.
Literatur
Wikimedia Foundation.
