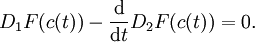- Lineares Funktional
-
Das Funktional bezeichnet in der Mathematik zumeist eine Funktion aus einem Vektorraum V in den Körper K, über dem der Vektorraum modelliert ist.
Oft ist V ein Funktionenraum, also ein Vektorraum, dessen Elemente reell- oder komplexwertige Funktionen sind. Ein Funktional ist somit eine Funktion auf Funktionen. Der mathematische Teilbereich der Funktionalanalysis bekam seinen Namen, da er historisch aus dem Studium solcher Funktionale hervorging.
Als grundlegende Unterscheidung ist es sinnvoll, lineare und nichtlineare Funktionale gesondert zu betrachten, da diese beiden Arten von Funktionalen auf sehr unterschiedliche Weise in der Mathematik behandelt werden. In beiden Fällen beschränken wir uns hier auf die fast ausschließlich untersuchten Fälle, in denen der Zahlenkörper (Skalarkörper) der Körper der reellen Zahlen K=R oder der Körper der komplexen Zahlen K=C ist.
Inhaltsverzeichnis
Einfache Beispiele
Ein einfaches lineares Funktional auf dem Vektorraum der Funktionen auf der reellen Achse ist das Auswertungsfunktional an der Null, das so genannte Dirac-Delta:
Ein einfaches nichtlineares Funktional auf dem Vektorraum der Kurven im Raum, speziell hier stetig differenzierbare Funktionen von [0,1] nach R3, ist das Bogenlängenfunktional:
Lineare Funktionale
In den meisten Bereichen der Funktionalanalysis, etwa in der Theorie der topologischen Vektorräume, wird der Begriff Funktional (ohne weiteren Zusatz) als Synonym für lineare Funktionale benutzt. Ein solches Funktional ist definitionsgemäß eine lineare Abbildung des Vektorraumes V in seinen Skalarkörper K. Die Menge all dieser Funktionale ist wiederum in natürlicher Form ein Vektorraum über dem gleichen Körper K, indem man für zwei Elemente f und g aus V die Addition und Skalarmultiplikation punktweise definiert, d. h.
Der Vektorraum der linearen Funktionale auf dem Vektorraum V wird der algebraische Dualraum genannt und oft mit V* bezeichnet.
Beispiele von Dualräumen
Für den Vektorraum V=Rn ist der Dualraum kanonisch isomorph zum Vektorraum selbst, d. h.
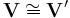 . Der kanonische Isomorphismus
. Der kanonische Isomorphismus 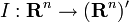 wird dabei über das kanonische Skalarprodukt vermittelt:
wird dabei über das kanonische Skalarprodukt vermittelt:Für den Vektorraum V=Cn gilt ähnliches wie im ersten Fall, allerdings ist die kanonische Abbildung
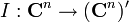 in diesem Fall antilinear:
in diesem Fall antilinear:Der Dualraum ist in diesem Fall also gleich groß, hat aber bezüglich der kanonischen Abbildung eine andere Skalarmultiplikation. Im Sinne der linearen Algebra sagt man auch der Dualraum ist kanonisch isomorph zum komplex konjugierten Vektorraum.
Für allgemeine endlichdimensionale Vektorräume kann man durch die Wahl einer Basis und Anwendung der beiden ersten Fälle zeigen, dass der Dualraum immer die gleiche Dimension wie der Ursprungsraum hat. Die Abbildungen zwischen dem Vektorraum und dem Dualraum sind dann aber im Allgemeinen nicht kanonisch.
Für unendlichdimensionale Vektorräume ist der Fall wesentlich komplizierter. In einigen wichtigen Fällen, z. B. für Hilberträume, ist der Vektorraum zwar ein kanonischer Unterraum, im Allgemeinen gilt dies allerdings nicht. Der algebraische Dualraum eines unendlichdimensionalen Vektorraums hat zudem immer größere Dimension (im Sinne der Kardinalität einer algebraischen Basis) als der Ursprungsraum.
Stetige lineare Funktionale
Wie gerade gesehen, ist der algebraische Dualraum eines unendlichdimensionalen Vektorraums immer größer als der ursprüngliche Vektorraum. Man kann sogar behaupten, dass diese Dualräume oft riesig sind und viele Elemente enthalten, die mathematisch kaum handhabbar sind. Das Ziel der Funktionalanalysis ist es allerdings, die Methoden der mehrdimensionalen Analysis auf unendlichdimensionale Räume auszudehnen und dabei insbesondere Konzepte wie Stetigkeit und Differenzierbarkeit zu untersuchen. Daher werden a priori nur Vektorräume betrachtet, die zumindest den Stetigkeitsbegriff sinnvoll zulassen. Dies sind die topologischen Vektorräume, zu denen alle normierten Vektorräume, insbesondere Banachräume, und Hilberträume gehören.
In einem topologischen Vektorraum sind nun im Allgemeinen nicht alle linearen Funktionale stetig. Die Menge der stetigen Funktionale, die in der Funktionalanalysis von primärem Interesse ist, heißt der topologische Dualraum und wird mit V bezeichnet.
Beispiele topologischer Dualräume
Für endlichdimensionale Vektorräume gibt es eine natürliche Topologie, die aus der euklidischen Norm hervorgeht (genauer gesagt: aus einer beliebigen euklidischen Norm, wenn man eine Basis wählt.). Dies ist gerade die Topologie die der normalen Standard-Analysis zugrunde liegt und in dieser ist jedes lineare Funktional stetig. Das heißt, der algebraische Dualraum ist gleich dem topologischen Dualraum.
Im unendlichdimensionalen Fall ist der topologische Dualraum (fast) immer ein echter Teilraum des algebraischen Dualraumes.
In normierten Vektorräumen ist ein Funktional f genau dann stetig, wenn es beschränkt ist, d. h.
Der topologische Dualraum ist dann automatisch ein Banachraum mit der oben angegebenen Supremumsnorm.
In Hilberträumen ist der topologische Dualraum kanonisch mit dem Ursprungsraum identifizierbar (Rieszscher Darstellungssatz). Die Identifikation erfolgt wie im endlichdimensionalen Fall über das Skalarprodukt:
Der topologische Dualraum des Raumes der unendlich oft stetig differenzierbaren Funktionen mit kompaktem Träger auf der reellen Achse (die so genannten Testfunktionen) mit einer bestimmten (hier nicht näher erklärten) Topologie wird als Raum der Distributionen bezeichnet. In diesem Raum liegt auch das weiter oben genannte Beispiel des Dirac-Delta-Funktionals.
Nichtlineare Funktionale
Nichtlineare Funktionale traten historisch erstmals in der Variationsrechnung auf. Ihr Studium unterscheidet sich grundlegend von dem der oben beschriebenen linearen Funktionale. In der Variationsrechnung setzt man es sich beispielsweise zum Ziel, die Extremalpunkte solcher Funktionalpunkte zu bestimmen. Zu diesem Zweck benötigt man eine Verallgemeinerung des Ableitungsbegriffs der mehrdimensionalen Analysis, d. h. eine Definition des Differentials des Funktionals. In der Variationsrechnung und in den Anwendungen ist dieses Differential unter dem Namen Variationsableitung bekannt, mathematisch präzisiert wird der Begriff z. B. durch die Fréchet-Ableitung und die Gateaux-Ableitung.
Beispiele von nichtlinearen Funktionalen
Große Bedeutung in der Anwendung, insbesondere in der klassischen Mechanik haben nichtlineare Funktionale auf Kurvenräumen, wie in dem Beispiel des Bogenlängenfunktionals weiter oben. Man kann dieses Beispiel leicht verallgemeinern.
Wir betrachten wiederum einen Kurvenraum und zusätzlich eine stetig differenzierbare Funktion
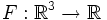 . Damit definieren wir:
. Damit definieren wir:Man sagt, das Funktional L habe einen stationären Punkt bei einer Kurve c, wenn das Differential
für alle Variationen h, das sind Kurven mit Anfangs- und Endpunkt in der Null, verschwindet. Dies ist hier genau dann der Fall, wenn das (gewöhnliche) Differential von F auf der ganzen Kurve c verschwindet:
- DF(c(t)) = 0.
Betrachtet man einen Kurvenraum und zweifach stetige Funktionen mit zwei Argumenten
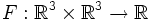 , so erhält man analog:
, so erhält man analog:stationären Punkte bei einer Kurve c, wenn das Differential
für alle Variationen h, verschwindet. Dies ist in diesem einfachen Fall genau dann der Fall, wenn c die Euler-Lagrange-Gleichung erfüllt, d. h.
Bisweilen, insbesondere in anwendungsnahen Texten, schreibt man eine funktionale Abhängigkeit (im Gegensatz zu der gewöhnlichen funktionellen Abhängigkeit) mit eckigen oder geschweiften statt mit runden Klammern und nennt dabei eventuell ein Dummy-Argument der Argumentfunktion, also I[f] oder I{f(x)} statt I(f).
Literatur
- Siegfried Großmann: Funktionalanalysis im Hinblick auf Anwendung in der Physik, AULA Verlag, 4. Aufl. 1988, ISBN 978-3891044797
Wikimedia Foundation.

![\delta:\mathfrak{F}(\mathbb{R},\mathbb{K})\to\mathbb{K} \quad
f\mapsto \delta[f]=f(0).](/pictures/dewiki/52/4d9a814e8326bb9711275a750e52131d.png)
![L:\mathcal{C}^1([0,1],\mathbb{R}^3)\to\mathbb{R} \quad
c\mapsto L[c]=\int_0^1 \|\dot{c}(t)\| \mathrm{d}t.](/pictures/dewiki/54/68edf5e8db8001311f290a896c38191b.png)
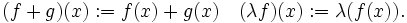
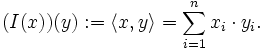
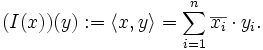
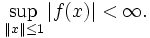
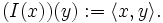
![L:\mathcal{C}([0,1],\mathbb{R}^3)\to\mathbb{R} \quad c\mapsto L[c]=\int_0^1 F(c(t)) \mathrm{d}t.](/pictures/dewiki/101/eead97e6ab46314e02cef4cb14a54d56.png)
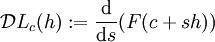
![L:\mathcal{C}^1([0,1],\mathbb{R}^3)\to\mathbb{R} \quad c\mapsto L[c]=\int_0^1 F(c(t),\dot{c}(t)) \mathrm{d}t,](/pictures/dewiki/101/e34bd8980920845c36c0364232742702.png)