Antiliminale C*-Algebra

Liminale C*-Algebren sind eine in der Mathematik betrachtete Klasse von C*-Algebren.

Diese C*-Algebren werden von manchen Autoren auch CCR-Algebren (CCR steht für completely continuous representations, d.h. kompakte Darstellungen) genannt, unter diesem Namen wurden sie 1951 von Irving Kaplansky eingeführt. Es besteht jedoch dann ein Namenskonflikt zu in der Quantenfeldtheorie betrachteten Algebren (CCR steht dort für canonical commutation relations, d.h. kanonische Vertauschungsrelationen). Wir schließen uns hier der auf Jacques Dixmier zurückgehenden Benennung an (frz.: liminaire, engl.: liminal).

Definition

Eine C*-Algebra heißt liminal, wenn die Bilder irreduzibler Darstellungen aus kompakten Operatoren bestehen.

Beispiele

• Duale C*-Algebren sind liminal.
• Kommutative C*-Algebren sind liminal, denn jede irreduzible Darstellung ist eindimensional. Die kommutative C*-Algebra C[0,1] der stetigen Funktionen $[0,1]\rightarrow \C$ ist liminal, aber nicht dual.
• Ist X lokalkompakt, so ist 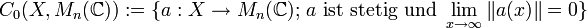$C_0(X,M_n(\C)) := \{a:X\rightarrow M_n(\C);\,a\mbox{ ist stetig und }\lim_{x\to\infty}\|a(x)\| = 0\}$ liminal, denn jede irreduzible Darstellung hat bis auf Äquivalenz die Form 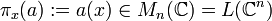$\pi_x(a) := a(x) \in M_n(\C) = L(\C^n)$ für ein $x\in X$.
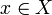• Es sei H ein unendlich-dimensionaler Hilbertraum. Dann ist A = L(H) nicht liminal, denn 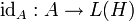$\mbox{id}_A:A\rightarrow L(H)$ ist irreduzibel und hat nicht-kompakte Operatoren im Bild.

Das größte liminale Ideal

Ist A eine C*-Algbra, so ist

$I:=\{a\in A; \pi(a)\,\mbox{ ist kompakt für jede irreduzible Darstellung von}\, A\}$

ein abgeschlossenes, zweiseitiges Ideal, das liminal ist und jedes andere liminale Ideal enthält, kurz das größte liminale Ideal. Demnach ist eine C*-Algebra genau dann liminal, wenn sie mit ihrem größten liminalen Ideal zusammenfällt. Der Quotient A / I kann durchaus wieder ein von {0} verschiedenes liminales Ideal enthalten; diese Beobachtung führt zum wichtigen Begriff der postliminalen C*-Algebra.

Eigenschaften

• Jede Unter-C*-Algebra einer liminalen C*-Algebra ist wieder liminal.
• Ist A eine liminale C*-Algebra und 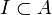$I\subset A$ ein abgeschlossenes zweiseitiges Ideal, so ist A / I wieder liminal.
• Ist A eine liminale C*-Algebra und 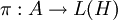$\pi:A\rightarrow L(H)$ eine irreduzible Darstellung, so gilt π(A) = K(H). Dabei ist K(H) die Algebra der kompakten Operatoren auf H, die Definition verlangte nur die Inklusion $\pi(A) \subset K(H)$.

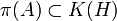Antiliminale C*-Algebren

Eine C*-Algebra A heißt antiliminal, wenn das einzige liminale Ideal in A das Nullideal ist, das heißt wenn das größte liminale Ideal {0} ist. Die Calkin-Algebra ist ein Beispiel für eine antiliminale C*-Algebra.

C*-Algebren mit stetiger Spur

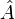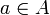Für eine C*-Algebra A sei $\hat{A}$ das Spektrum von A, das heißt die Menge aller Äquivalenzklassen [π] irreduzibler Darstellungen π von A (siehe Hilbertraum-Darstellung). Ist $[\pi]\in \hat{A}$ und $a\in A$ positiv, so ist π(a) ein positiver kompakter Operator auf H und man kann die Spur $Sp(\pi(a))\in [0,\infty]$ bilden, wobei diese Zahl nicht von π sondern nur von der Äquivalenzklasse [π] abhängt. Sei weiter

$P:=\{a\in A;\, a \ge 0,\, [\pi]\mapsto Sp(\pi(a)) \mbox{ ist eine stetige Funktion }\,\hat{A}\rightarrow [0,\infty)\}$.

Dann ist die Menge aller 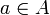$a\in A$, für die 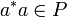$a^*a\in P$ gilt, ein zweiseitiges Ideal in A. Wenn dieses Ideal dicht in A liegt, so sagt man, A sei eine C*-Algebra mit stetiger Spur. Es gilt folgender Satz.

• C*-Algebren mit stetiger Spur sind liminal, das Spektrum einer solchen C*-Algebra ist ein Hausdorffraum.

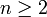Die oben genannte C*-Algebra $C([0,1],M_n(\C))$ ist ein Beispiel für eine C*-Algebra mit stetiger Spur. Die Unter-C*-Algebra $\{a\in C([0,1],M_n(\C));\, a(0) \mbox{ ist eine Diagonalmatrix} \}$ ist keine C*-Algebra mit stetiger Spur (für $n \ge 2$), aber als Unteralgebra natürlich liminal.

Quellen

• W. Arveson: Invitation to C*-algebras, ISBN 0387901760
• J. Dixmier: Les C*-algèbres et leurs représentations, Gauthier-Villars, 1969