- 1'-Akzeptanz
-
Der Staiger-Wagner-Automat (benannt nach Ludwig Staiger und Klaus Wagner) ist ein ω-Automat und bildet ein Analogon zum Muller-Automaten. Die von Staiger-Wagner-Automaten erkannten Sprachen sind eine Untermenge der ω-regulären Sprachen.
Inhaltsverzeichnis
Formale Definition
Ein Staiger-Wagner-Automat ist ein 5-Tupel
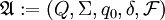 mit
mit- Q Zustandsmenge
- Σ Eingabealphabet
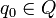 Startzustand
Startzustand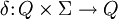 Transitionsfunktion.
Transitionsfunktion.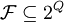 und
und 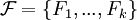 für
für 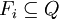
Eigenschaften
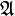 akzeptiert
akzeptiert 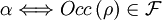 (z.B.
(z.B. 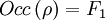 oder ... oder
oder ... oder 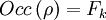 ) gilt für den Lauf ρ von
) gilt für den Lauf ρ von 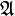 auf dem Wort α.
auf dem Wort α.Eine ω-Sprache ist Staiger-Wagner-erkennbar, gdw. sie eine boolesche Kombination von E-erkennbaren ω-Sprachen ist. Sie ist außerdem Staiger-Wagner-erkennbar, gdw. sie deterministisch Büchi-erkennbar und deterministisch co-Büchi-erkennbar ist.
Beispiel
Sei
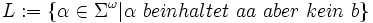 eine ω-Sprache über Σ = {a,b,c}
eine ω-Sprache über Σ = {a,b,c}Ein deterministischer Staiger-Wagner-Automat, der L erkennt ist dann z.B.:
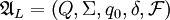 mit
mit 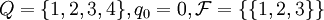 und
und
δ = {1/a → 2, 1/b → 4, 1/c → 1,
2/a → 3, 2/b → 4, 2/c → 1,
3/a → 3, 3/b → 4, 3/c → 3,
4/a → 4, 4/b → 4, 4/c → 4}Genau dann wenn der Automat die Zustände 1, 2 und 3 aber nicht 4 besucht, wird α akzeptiert.
Verwandte Akzeptanzbedingungen
Mit der Staiger-Wagner-Bedingung sind die beiden folgenden Akzeptanzbedingungen nahe verwandt.
1-Akzeptanz
Hier gibt es nur eine Menge F akzeptierender Zustände und die Bedingung ist
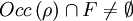 .
.1'-Akzepztanz
Auch hier gibt es nur eine Menge akzeptierender Zustände und die Bedingung lautet
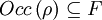 .
.Transformation in einen Büchi-Automaten
Um einen Staiger-Wagner-Automaten in einen Büchi-Automaten, der dieselbe Sprache erkennt, zu transformieren, werden im Allgemeinen exponentiell viele Zustände gebraucht. Diese Explosion der Zustandsmenge entfällt bei 1-Akzeptanz und 1'-Akzeptanz.
Literatur
- Ludwig Staiger und Klaus W. Wagner , Automatentheoretische und automatenfreie Characterisierungen topologischer Klassen regulärer Folgemengen, Elektronische Informationsverarbeitung und Kybernetik EIK, 10 (1974) 379–392.
- Erich Grädel, Wolfgang Thomas und Thomas Wilke (Herausgeber), Automata, Logics, and Infinite Games, LNCS 2500, 2002, Seite 20 (auf englisch)
Wikimedia Foundation.

