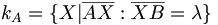- Apollonische Kreise
-
In der Geometrie ist der Kreis des Apollonios (auch Kreis des Apollonius oder apollonischer Kreis) ein spezieller geometrischer Ort, nämlich die Menge aller Punkte, für die das Verhältnis der Entfernungen zu zwei vorgegebenen Punkten einen vorgegebenen Wert hat. Der Kreis des Apollonios ist nicht zu verwechseln mit dem apollonischen Problem, einem Berührkreis-Problem. Namensgeber ist in beiden Fällen Apollonios von Perge.
Satz und Definition
- Gegeben seien eine Strecke [AB] und eine positive reelle Zahl
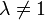 . Dann ist die Punktmenge
. Dann ist die Punktmenge
ein Kreis, der als Kreis des Apollonios bezeichnet wird.
Zur Begründung der Kreiseigenschaft verwendet man den inneren und den äußeren Teilungspunkt der Strecke [AB] im Verhältnis λ. Diese beiden Punkte (Ti und Ta) erfüllen die oben geforderte Bedingung und teilen die Strecke [AB] harmonisch. Ist nun X ein beliebiger Punkt mit der Eigenschaft
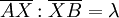 , so teilt die Gerade XTi die gegebene Strecke [AB] im Verhältnis
, so teilt die Gerade XTi die gegebene Strecke [AB] im Verhältnis 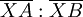 . XTi muss daher mit der Winkelhalbierenden des Winkels AXB übereinstimmen. Entsprechend lässt sich zeigen, dass die Gerade XTa den Nebenwinkel von
. XTi muss daher mit der Winkelhalbierenden des Winkels AXB übereinstimmen. Entsprechend lässt sich zeigen, dass die Gerade XTa den Nebenwinkel von 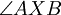 halbiert. Da die Winkelhalbierenden von Nebenwinkeln zueinander senkrecht stehen, muss X auf dem Thaleskreis über [TiTa] liegen.
halbiert. Da die Winkelhalbierenden von Nebenwinkeln zueinander senkrecht stehen, muss X auf dem Thaleskreis über [TiTa] liegen.Umgekehrt erfüllt jeder Punkt X des genannten Thaleskreises die Bedingung
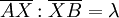 .
.Im speziellen Fall λ = 1 ist die gesuchte Punktmenge die Mittelsenkrechte der Punkte A und B.
Weitere Eigenschaften
- Der Radius des Apollonios-Kreises beträgt
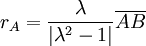 .
.
- Der durch Ti gehende Apollonioskreis für die Strecke [AB] ist der durch Ti gehende Inversionskreis, bezogen auf den die Endpunkte A,B zueinander invers sind.
- Wenn A und B bei Inversion am Apollonioskreis ineinander übergehen, wird jeder durch A und B gehende Kreis ebenfalls in sich selbst invertiert, und schneidet den Apollonioskreis deshalb rechtwinklig, insbesondere auch der über [AB] geschlagene Kreis. Wegen der Reziprozität der harmonischen Teilung - teilt ein Punktpaar ein anderes (sc. die von dem andern gebildete Strecke) harmonisch, so ist es selbst von diesem harmonisch geteilt (im Verhältnis
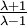 statt λ ) - ist der Kreis über [AB] Apollonioskreis für die Strecke [TiTa].
statt λ ) - ist der Kreis über [AB] Apollonioskreis für die Strecke [TiTa].
Weblinks
- Gegeben seien eine Strecke [AB] und eine positive reelle Zahl
Wikimedia Foundation.