- Archimedeszahl
-
Die Archimedes-Zahl ist eine dimensionslose Kennzahl, benannt nach dem antiken Gelehrten Archimedes. Sie kann als Verhältnis von Auftriebskraft zu Reibungskraft interpretiert werden, und ist definiert als
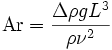 .
.
Formelzeichen Bezeichnung SI-Einheit ρ Dichte 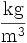
g Erdbeschleunigung 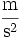
L charakteristische Länge m ν kinematische Viskosität 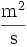
In älteren Texten (beispielsweise dem Vorlesungsmanuskript von Prof. Renz der RWTH Aachen WS 2002/2003, Link leider nicht verfügbar) findet sich auch eine andere Definition der Archimedes-Zahl, welche als das Verhältnis von Auftriebskraft zu Trägheitskraft gedeutet werden kann:
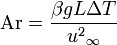 mit
mit
Formelzeichen Bezeichnung SI-Einheit β isobarer Ausdehnungskoeffizient 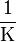
g Erdbeschleunigung 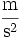
L charakteristische Länge m ΔT treibende Temperaturdifferenz : 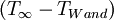
K 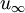
Umgebungs-Geschwindigkeit 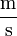
Diese Definition ist identisch mit der Definition der Richardson-Zahl.
Wikimedia Foundation.
