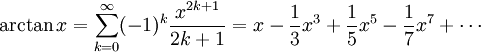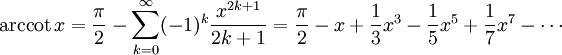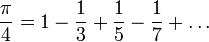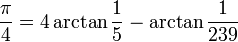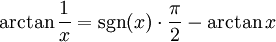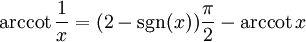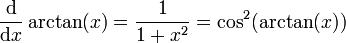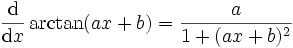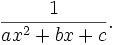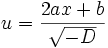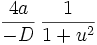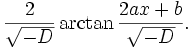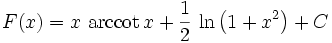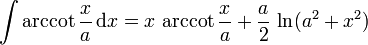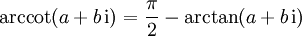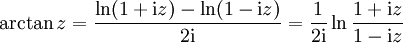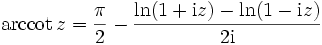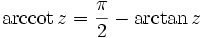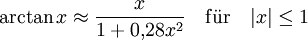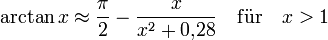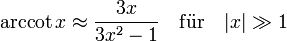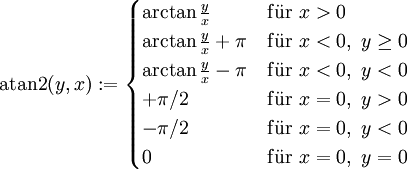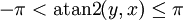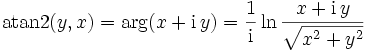- Arctan
-
Arkustangens und Arkuskotangens sind mathematische Funktionen. Sie sind die Umkehrfunktionen des Tangens bzw. des Kotangens und damit Arkusfunktionen. Da der Tangens periodisch ist, wird zur Umkehrung der Definitionsbereich von Tangens auf ( − π / 2,π / 2) beschränkt. Beim Arkuskotangens erfolgt eine Beschränkung auf
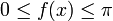 .
.Inhaltsverzeichnis
Eigenschaften
Arkustangens Arkuskotangens Definitionsbereich 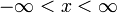
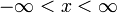
Wertebereich 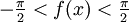
0 < f(x) < π Monotonie streng monoton steigend streng monoton fallend Symmetrien Ungerade Funktion: arctan( − x) = − arctanx Punktsymmetrie zu 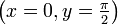
arccotx = π − arccot( − x)Asymptoten 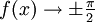 für
für 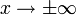
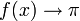 für
für 
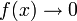 für
für 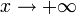
Nullstellen x = 0 keine Sprungstellen keine keine Polstellen keine keine Extrema keine keine Wendepunkte (0;0) 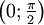
Spezielle Werte
x 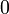
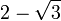
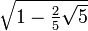
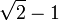
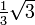
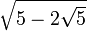
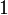
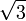
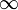
arctan(x) 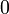
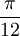
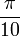
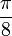
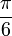
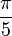
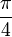
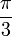
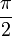
Wegen der Punktsymmetrie gelten die entsprechenden Wertepaare auch im Negativen. Solche speziellen Werte gibt es unendlich viele, aufgelistet sind nur die einfachsten.
Reihenentwicklung
Die Taylorreihe des Arkustangens mit dem Entwicklungspunkt x=0 lautet:
Die Taylorreihe des Arkuskotangens mit dem Entwicklungspunkt x=0 lautet:
Diese Reihen konvergieren genau dann, wenn
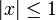 und
und 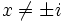 ist. Zur Berechnung des Arkustangens für
ist. Zur Berechnung des Arkustangens für 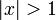 kann man ihn auf einen Arkustangens von kleineren Argumenten zurückführen. Dazu kann man entweder die Funktionalgleichung hernehmen, oder (um ohne π auszukommen) die Gleichung
kann man ihn auf einen Arkustangens von kleineren Argumenten zurückführen. Dazu kann man entweder die Funktionalgleichung hernehmen, oder (um ohne π auszukommen) die GleichungHiermit lässt sich das Argument nach mehrfacher Anwendung beliebig verkleinern, was eine sehr effiziente Berechnung durch die Reihe ermöglicht.
Berechnung der Kreiszahl
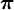 mit Hilfe des Arkustangens
mit Hilfe des ArkustangensDie Reihenentwicklung kann zur näherungsweisen Berechnung der Zahl π verwendet werden: Die einfachste Formel ist der Spezialfall x = 1, die Leibniz-Formel
Da sie nur sehr langsam konvergiert, verwendete John Machin 1706 die kompliziertere Formel
um die ersten 100 Nachkommastellen von π zu berechnen. Letztere konvergiert schneller und wird auch heute noch für die Berechnung von π verwendet.
Funktionalgleichung
Die Arkustangenswerte über 1 oder unter -1 lassen sich aus den Werten zwischen -1 und 1 ableiten:
Die Arkuskotangenswerte über 1 oder unter -1 lassen sich aus den Werten zwischen -1 und 1 ableiten:
Ableitungen
Arkustangens:
Arkuskotangens:
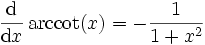 .
.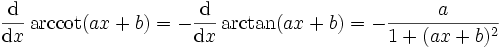
Stammfunktionen
Arkustangens:
Der Arkustangens spielt eine wesentliche Rolle bei der symbolischen Integration von Ausdrücken der Form
Ist die Diskriminante D = b2 − 4ac nicht negativ, so kann man eine Stammfunktion mittels Partialbruchzerlegung bestimmen. Ist die Diskriminante negativ, so kann man den Ausdruck durch die Substitution
in die Form
bringen; eine Stammfunktion ist also
Eine Stammfunktion des Arkustangens selbst ist
Arkuskotangens:
Komplexes Argument
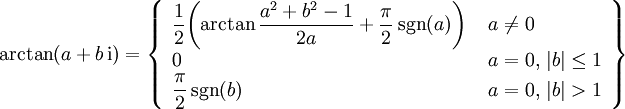
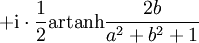 mit
mit 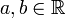
Anmerkungen
Arkustangens:
Man kann den Arkustangens durch den komplexen Logarithmus ausdrücken:
Arkuskotangens:
Man kann den Arkuskotangens durch einen komplexen Logarithmus ausdrücken:
Zwischen Arkustangens und Arkuskotangens besteht folgende Beziehung:
Näherungsweise Berechnung
Es gelten folgende Näherungen:
Arkustangens (maximale Abweichung unter 0,005 Radianten):
Weitere Informationen dazu und eine genauere Approximation hier.
Arkuskotangens:
Der „Arkustangens“ mit zwei Argumenten (atan2)
Diese Funktion dient bei der Umrechnung von kartesischen Koordinaten P(x;y) in Polarkoordinaten
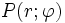 der Ermittlung des Winkels
der Ermittlung des Winkels 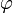 . Da der Arkustangens mit einfachem Argument nicht die Möglichkeit bietet, den Winkel im korrekten Quadranten zu ermitteln, und außerdem die Tangensfunktion für einen Funktionswert von
. Da der Arkustangens mit einfachem Argument nicht die Möglichkeit bietet, den Winkel im korrekten Quadranten zu ermitteln, und außerdem die Tangensfunktion für einen Funktionswert von 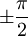 nicht umkehrbar ist, gibt es in verschiedenen Programmiersprachen (z. B. in C, Fortran) eine Funktion, die mit 2 Argumenten aufgerufen wird. Sie wird üblicherweise mit
nicht umkehrbar ist, gibt es in verschiedenen Programmiersprachen (z. B. in C, Fortran) eine Funktion, die mit 2 Argumenten aufgerufen wird. Sie wird üblicherweise mit 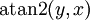 o. Ä. bezeichnet.
o. Ä. bezeichnet.Die Funktion
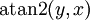 kann über die folgende Eigenschaft definiert werden: Sind x,y reelle Zahlen und
kann über die folgende Eigenschaft definiert werden: Sind x,y reelle Zahlen und 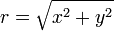 , so gilt:
, so gilt: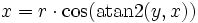
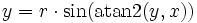
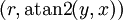 sind hierbei die Polarkoordinaten des Punktes mit den kartesischen Koordinaten (x,y).
sind hierbei die Polarkoordinaten des Punktes mit den kartesischen Koordinaten (x,y).Definition
Eine von mehreren in der Praxis vorkommenden Definitionen:
Für x = y = 0 ist die Funktion manchmal nicht definiert. Auch Sonderfälle wie Not a Number und Inf werden unterschiedlich behandelt.
Wertebereich
Bei der o. g. Definition:
Anmerkungen
Eine weitere Möglichkeit besteht darin, die Funktion
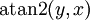 für (x,y) ≠ (0,0) über den Hauptwert des komplexen Logarithmus zu definieren:
für (x,y) ≠ (0,0) über den Hauptwert des komplexen Logarithmus zu definieren:Diese Funktion wird zum Beispiel in der inversen Kinematik genutzt, um korrekte Gelenkeinstellungen berechnen zu können.
Siehe auch
Primäre trigonometrische Funktionen
Sinus und Kosinus | Tangens und Kotangens | Sekans und KosekansUmkehrfunktionen (Arkusfunktionen)
Arkussinus und Arkuskosinus | Arkustangens und Arkuskotangens | Arkussekans und ArkuskosekansHyperbelfunktionen
Sinus Hyperbolicus und Kosinus Hyperbolicus | Tangens Hyperbolicus und Kotangens Hyperbolicus | Sekans Hyperbolicus und Kosekans HyperbolicusAreafunktionen
Areasinus Hyperbolicus und Areakosinus Hyperbolicus | Areatangens Hyperbolicus und Areakotangens Hyperbolicus | Areasekans Hyperbolicus und Areakosekans Hyperbolicus
Wikimedia Foundation.