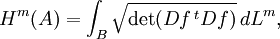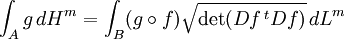- Areaformel
-
Unter der Flächenformel versteht man eine Integrationsregel für die Berechnung von Flächeninhalten m-dimensionaler Flächen im
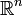 (m ≤ n), sie lautet
(m ≤ n), sie lautetwobei A = f(B) eine in parametrisierter Form vorliegende Fläche bezeichnet bei einer injektiven differenzierbaren Funktion
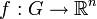 mit
mit 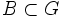 , G ein Gebiet im
, G ein Gebiet im 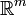 . Hm(A) ist das m-dimensionale Hausdorff-Maß (der m-dimensionale Flächeninhalt) von A und Lm das m-dimensionale Lebesgue-Maß (Volumenmaß) im
. Hm(A) ist das m-dimensionale Hausdorff-Maß (der m-dimensionale Flächeninhalt) von A und Lm das m-dimensionale Lebesgue-Maß (Volumenmaß) im 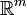 . Der Integrand wird die verallgemeinerte Jacobi-Determinante von f genannt; Df ist die Ableitung (Funktionalmatrix) von f und Df t deren Transponierte.
. Der Integrand wird die verallgemeinerte Jacobi-Determinante von f genannt; Df ist die Ableitung (Funktionalmatrix) von f und Df t deren Transponierte.Eine allgemeinere Formulierung der Flächenformel lautet
und liefert den Wert des Integrals einer auf der Fläche A definierten Funktion g nach dem Hausdorff-Maß Hm.
Als Voraussetzungen für diese Formeln sind Lm-Messbarkeit von B und Hm-Messbarkeit von g zu nennen, was allerdings keine wesentliche Einschränkung bedeutet, da alle in der Praxis vorkommenden Mengen bzw. Funktionen diese Eigenschaft besitzen.
Im Spezialfall m = n ergibt die Flächenformel die Transformationsformel aus der Maß- und Integrationstheorie.
Literatur
- Herbert Federer: Geometric Measure Theory. Grundlehren der mathematischen Wissenschaften, Vol. 153, Springer-Verlag Berlin Heidelberg New York, 1969
Wikimedia Foundation.