- Angriffsmoment
Angriffsmoment in einem beliebigen Querschnitt x eines Stabes heißt das resultierende Moment Mx der äußeren Kräfte auf einer Seite von x in bezug auf den der Stabachse angehörigen Punkt dieses Querschnitts.
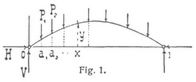
So hat man z.B. in dem durch Fig. 1 angedeuteten Falle, wenn die Pfeile äußere Kräfte vertreten:
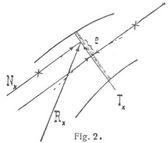
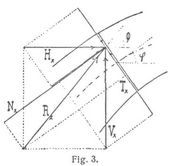
Das Angriffsmoment ist hiernach auch das Moment der resultierenden Kraft Rx, mit welcher der Stahlen auf der einen Seite des Querschnitts x auf den Stahlen auf der andern Seite desselben wirkt, in Hinsicht auf den Achspunkt des Querschnitts. Da das Moment Mx eine Biegung des Stabes zur Folge hat (s. Biegung), so wird Mx auch mitunter Biegungsmoment genannt. Im folgenden setzen wir gerade oder einfach gekrümmte Stäbe (s. Achse eines Stabes) mit gegenüber den ursprünglichen Abmessungen verschwindenden Formänderungen voraus. Die resultierende Schnittkraft Rx kann nach Angriffspunkt (im Querschnitt), Größe und Richtung verschieden sein. Sie läßt sich jedoch stets zerlegen in eine Komponente Nx normal dem Querschnitt und eine Komponente Tx längs desselben (Fig. 2), welche die Normalkraft und Transversalkraft oder Tangentialkraft des Querschnitts heißen. Denkt man sich im Achspunkte des letzteren zwei Kräfte parallel und numerisch gleich Nx, aber von entgegengesetzten Richtungen hinzugebracht (Fig. 2), wodurch am Gleichgewicht (oder der Bewegung) nichts geändert wird, so erkennt man, daß Rx ersetzt werden kann durch eine in der Achse wirkende Kraft Nx (Axialkraft), die in der Querschnittsebene wirkende Kraft Tx und ein Kräftepaar vom Moment Mx = eNx. Das Angriffsmoment ist also für die betrachteten kleinen Formänderungen auch das Moment der Normalkraft Nx in bezug auf den Achspunkt des Querschnitts. Die Gesamtheit der Angriffspunkte von Nx oder Rx in allen Querschnitten bildet eine stetige Linie, welche die Stützlinie genannt wird und besonders bei Bogenträgern (s.d.) eine Rolle spielt. Sind Vx, Hx die Vertikalkomponente und Horizontalkomponente von Rx, und φ der Neigungswinkel der Stabachse gegen eine horizontale x-Achse, so hat man (Fig. 3)
Nx = Vx sin φ + Hx cos φ,
Tx = Vx cos φ – Hx sin φ.
Die Ausdrücke von Mx, Vx, Hx sind von der Anordnung des Stabs und der Stützen, sowie von den äußeren Kräften abhängig (s. Balken, Bogen und [1], [2]). Sind alle äußeren Kräfte einschließlich der Stützenreaktionen vertikal, so folgen mit Hx = 0
Nx = Vx sin φ, Tx = Vx cos φ,
und bei horizontaler Stabachse mit φ = 0
Νx = 0, Tx = Vx
(horizontale Balken). Wenn in letzterem Falle das Angriffsmoment nicht Null ist, so muß nach dem Ausdrucke Mx = eNx für dasselbe e = ∞ sein. Bezüglich der Erweiterung des Begriffs der Angriffsmomente mit Rücksicht auf Fachwerke u.s.w. s. Schnittkräfte und [3], [4].
Literatur: [1] Weyrauch, Aufgaben zur Theorie elastischer Körper, Leipzig 1885, S. 89, 117, sowie S. 96, 129, 132 u.s.w. – [2] Ders., Die elastischen Bogenträger, München 1897, S. 4. – [3] Ders., Theorie der statisch bestimmten Träger für Brücken und Dächer, Leipzig 1887, §§ 7–9. – [4] Ders., Beispiele und Aufgaben zur Berechnung der statisch bestimmten Träger für Brücken und Dächer, Leipzig 1888, S. 4 u. f.
Weyrauch.
http://www.zeno.org/Lueger-1904.