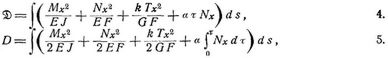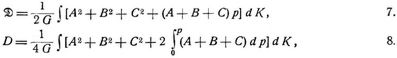- Verschiebungsarbeit
Verschiebungsarbeit (Formänderungsarbeit, Deformationsarbeit), die Arbeit D zur Ueberwindung der inneren Kräfte (Bd. 1, S. 103, Bd. 6, S. 333) während irgendwelcher Verschiebungen der Teile eines Körpers. Virtuelle Verschiebungsarbeit heißt die Arbeit D, welche zur Ueberwindung der inneren Kräfte nötig wäre, wenn die letzteren konstante Werte wie am Ende der Verschiebungen hätten. Bezüglich andrer, unzweckmäßiger Begriffsbestimmungen und Abarten der Verschiebungsarbeit s. [34].
Die Ausdrücke der Arbeiten D, D hängen von den in Betracht gezogenen Verschiebungen und inneren Kräften ab. Für ein beliebiges System materieller Punkte (Bd. 6, S. 333), zwischen welchen lediglich Kräfte S beliebiger Gesetze in den Verbindungsgeraden wirken, hat man während irgendwelcher Längenänderungen λ der letzteren [18], S. 182, 185:,
wobei die Summe Σ auf alle Verbindungsgeraden mit Kräften zu erstrecken ist. – Als ein derartiges System ist auch die Gesamtheit der Knotenpunkte eines beliebigen ebenen oder räumlichen Fachwerks unter den üblichen Voraussetzungen der Fachwerkstheorie (Bd. 3, S. 535) anzusehen. Bezeichnen s, F, E, S, α, τ die Längen, Querschnitte, Elastizitätsmoduln, Stabkräfte, linearen Ausdehnungskoeffizienten und Temperaturänderungen (gegenüber den Temperaturen im anfänglichen spannungslosen Zustande) der einzelnen Stäbe, wobei E, α als konstant gelten, dann hat man die Längenänderung eines Stabes [18], S. 213:
λ = S/E F s + α τ s,
und damit nach 1. für das ganze Stabsystem [18] S. 222:
worin die Summen Σ, alle Stäbe umfassen. Für einen einzelnen axial gezogenen oder gedrückten geraden Stab gelten also [18], S. 213:
wobei Biegung ausgeschlossen ist.
Unter den Voraussetzungen der technischen Biegungstheorie (Bd. 1, S. 792) mit Berücksichtigung des Einflusses der Querschubspannungen (Bd. 1, S. 797) ergeben sich für gerade und einfach gekrümmte Stäbe, wenn F, J, Mx, Nx, Tx, r, E, G, k, α, d s Querschnitt, Trägheitsmoment, Angriffsmoment, Normalkraft, Transversalkraft, Temperaturänderung, Elastizitätsmodul, Schubelastizitätsmodul, Koeffizient der Schubwirkung, Ausdehnungskoeffizient und Axdifferential bei x bedeuten [19], S. 204, 206:
worin das Glied mit Tx häufig vernachlässigt wird, was bei Bogenträgern (Bd. 2, S. 141, 153, 155) immer zulässig ist. Für horizontale Balkenträger (Bd. 1, S. 503, 507, 518) ist Tx = Vx, unter Vx die Vertikalkraft bei x verbanden, ferner bei horizontaler x-Achse d s = d x, und wenn wie gewöhnlich nur vertikale Aktivkräfte (Lasten u.s.w.) auf den Träger kommen Nx = 0, während für Ketten (Bd. 5, S. 448; Bd. 4, S. 710) und andre nur axial beanspruchte Stäbe Mx = 0, Tx = 0 sind. Ausdrücke von 5. für spezielle Fälle s. Biegungsarbeit, Bd. 2, S. 1. – Für einen lediglich auf Torsion beanspruchten prismatischen Stab der Länge l hat man unter den gewöhnlichen Voraussetzungen der Torsionstheorie (S. 574 ff.), wenn M das Torsionsmoment, ϑ den Torsionswinkel bezeichnet [19] S. 72:
D = ϑ l M, D = ϑ l/2 M.
6.
Betreffend Ausdrücke für spezielle Fälle s. Torsionsarbeit.
[778] Für einen beliebigen isotropen festen Körper, welchem der Elastizitätsmodul E und Schubelastizitätsmodul G (Bd. 3, S. 392), der Elastizitätsquotient ε (Bd. 3, S. 395), und an der Stelle des Volumenelements d K die Hauptspannungen A, B, C entsprechen (Bd. 4, S. 791), bestehen unter den gewöhnlichen Voraussetzungen der Elastizitätslehre (Bd. 3, S. 389) die Gleichungen [19] S. 202:
worin zur Abkürzung gesetzt ist:
und die Integration alle Volumenelemente zu umfassen hat. Spezielle Fälle von 7., 8. bilden die Ausdrücke 2. bis 5. Wie man steht, gilt im Falle isotroper Körper stets:
für τ = 0 D = 2 D.
10.
Die Gleichungen 7., 8. gelten übrigens auch für isotrope Körper, bei welchen nicht wie bei festen Körpern die Spannungen vor Eintritt von Verschiebungen gleich Null angenommen werden, in welchem Falle nur in dem Ausdrucke 9. von p die Anfangsspannung P zu addieren ist. Vgl. Bd. 3, S. 392 und [19], S. 158, 202. – Für vollkommene gasförmige und tropfbare Flüssigkeiten (Bd. 3, S. 391; Bd. 5, S. 544) ergeben sich beim Uebergange vom Volumen v0 zum Volumen v, wenn der Druck p im Innern überall als gleich gilt [19], S. 79:
D = p (v0 – v), D = – ∫ p d v.
11.
Spezielle Ausdrücke von D sind als – L aus Bd. 1, S. 102, zu entnehmen. Werte von D für reibende Flüssigkeiten s. [18], S. 160. – Für jeden beliebigen Körper hat man bei den Bd. 3, S. 389 eingeführten Bezeichnungen [18], S. 108:
worin die Integration auf alle Volumenelemente d K zu erstrecken ist, und unter den üblichen Voraussetzungen Xy = Yx, Yz = Zy, Zx = Xz ist (Bd. 3, S. 390). Vgl. Potential, elastisches, Bd. 7, S. 199. Die Ausdrücke 2. bis 11. lassen sich aus 12. bis 13. ableiten. – Beziehungen der Verschiebungsarbeit zu andern Größen s. [18], S. 100, [19], S. 71, 78.
In neuerer Zeit hat die Verschiebungsarbeit im Ingenieurwesen besonders durch das Prinzip der kleinsten Verschiebungsarbeit und die im Anschluß daran gewonnenen allgemeineren Beziehungen Bedeutung erlangt. Bei Fachwerken und sonstigen Konstruktionen treten häufig Größen X auf (Stabkräfte, Stützenreaktionen, Momente u.s.w.), von welchen die Verschiebungsarbeit mit abhängt, die aber durch die Statik allein, unabhängig von den Eigenschaften des Materials, nicht bestimmbar sind (vgl. Fachwerke, statisch unbestimmte, Bd. 3, S. 551, Träger, zusammengesetzte, S. 590, Balken, Bd. 1, S. 503, 507,518, Bogen, Bd. 2, S. 141, 153, 155 u.s.w.). Menabrea erkannte [1] und Castigliano bewies [2], daß diese Größen X für Fachwerke und beliebige isotrope feste Körper unter den üblichen Voraussetzungen so bestimmt sind, daß
∂D/∂X = 0 (womit ∂2D/∂X2 positiv),
d.h. daß die Verschiebungsarbeit ein Minimum wird. Vorausgesetzt war dabei, daß die Temperatur konstant und die Stützpunkte fest oder nur senkrecht zu den Reaktionen verschiebbar sind, so daß die letzteren während der Deformationen keine Arbeit leisten. Die Bedingungen zur Berechnung statisch unbestimmter Größen X wurden später auch auf Temperaturänderungen [7], [14] und Bewegungen der Stützpunkte [14], [19], S. 211, 213, 223, 233 ausgedehnt. Im folgenden seien sie in dieser Allgemeinheit gegeben. Vgl. bezüglich der Zweckmäßigkeit [34].
Es möge U die Arbeit der mit ihren Endwerten konstant gedachten, statisch unbestimmten Reaktionen während der betrachteten Verrückungen und ∂ U die Aenderung von U infolge einer Aenderung ∂ X der statisch unbestimmten Größe X bei konstanten Verrückungen bezeichnen. Die Bedingungsgleichung zur Berechnung einer statisch unbestimmten Größe X lautet dann im Falle 1:
Σλ∂S/∂X = ∂U/∂X,
14.
welche Formel auch für Fachwerke von beliebigen Beziehungen zwischen Stabkräften S und Längenänderungen λ gilt. Für die Fachwerke des Falles 2. aus prismatischen Stäben von konstantem E, α nimmt 14. die Form an:
Σ (S/E F + α τ) s ∂S/∂X = ∂U/∂X,
15.
In den Fällen 4., 5. eines geraden oder einfach gekrümmten, auf Biegung beanspruchten Stabes gilt die Bedingung:
und in dem Falle 7., 8. eines beliebigen isotropen Körpers:
Mit Rücksicht auf die Ausdrücke von D hat man in allen diesen Fällen bei festen Körpern:
wenn speziell τ = 0, U = 0, ∂D/∂X = 0,
18.
es tritt dann, wie schon erwähnt, das Prinzip der kleinsten Verschiebungsarbeit ein. Selbstverständlich ist stets U = 0, wenn die durch statisch unbestimmte Reaktionen ergriffenen Knotenpunkte[779] festliegen oder nur senkrecht zu jenen Reaktionen verschiebbar sind. Andernfalls sind die Beiträge zu U positiv oder negativ, je nachdem die Verrückungen in den Richtungen der betreffenden Reaktionen oder entgegengesetzt denselben stattfinden. Soll beispielsweise bei der Berechnung des Horizontalschubs X = H eines Zweigelenkbogens (Bd. 2, S. 164; Bd. 3, S. 553) eine Aenderung ∆ l der Spannweite berücksichtigt werden, so hat man, weil einer Zunahme ∆ l von l eine Bewegung entgegen H entsprechen würde:
U = – H ∆ l, ∂U/∂X = – ∆ l.
Wird ein Träger oder sonstiges materielles System betrachtet, welches aus mehreren der oben erwähnten Teile besteht, so hat man die den letzteren entsprechenden linken Seiten der Bedingungsgleichungen für die X zu addieren, während die rechte Seite ungeändert bleibt (vgl. Träger, zusammengesetzte, S. 590, wo auch Beispiele behandelt sind). Da man stets ebensoviel Bedingungsgleichungen vorstehender Formen anschreiben kann, als statisch unbestimmte Größen X auftreten, so lassen sich diese sämtlich berechnen. Näheres hierüber enthält die angeführte Literatur.
In obiger Darstellung sind Reibungen in Gelenken und Gleitungen, wie überhaupt Kräfte in Unstetigkeitsschnitten der Verrückungen wie üblich vernachlässigt. Wäre R die Arbeit dieser mit ihren Endwerten konstant gedachten Kräfte, so würde behufs ihrer Berücksichtigung in 14. bis 17. U + R an Stelle von U zu setzen sein [14], [19] S. 211, 213. Alle für feste Körper unter den üblichen Voraussetzungen angeführten Beziehungen gelten nur für elastische Verschiebungen bei konstanten Elastizitätsmoduln E, G (vgl. Bd. 3, S. 382, 383, 392) und konstanten Ausdehnungskoeffizienten α (Bd. 1, S. 392). Bezüglich der Arbeiten zur Ueberwindung der inneren Kräfte bei beliebigen Verschiebungen fester Körper s. Proportionale Widerstände, Bd. 7, S. 269.
Literatur: [1] Menabrea, Nouveau principe sur la distribution des tensions dans les systemes élastiques, Comptes rendus 1858, XLVI, S. 1056 (s.a. 1885, XCVIII, S. 714). – [2] Castigliano, Theorie de l'equilibre des systemes élastiques et ses applications, Turin 1880 (deutsch von Hauff, Wien 1886). – [3] Fränkel, Das Prinzip der kleinsten Arbeit der inneren Kräfte elastischer Systeme und seine Anwendung auf die Lösung baustatischer Aufgaben, Zeitschr. d. Arch.- u. Ing.-Vereins zu Hannover 1882, S. 63. – [4] Koenen, Vereinfachung der Berechnung kontinuierlicher Balken mit Hilfe des Satzes von der Arbeit, Wochenbl. f. Arch. u. Ing. 1882, S. 402, 416. – [5] Müller-Breslau, Ueber die Anwendung des Prinzips der Arbeit in der Festigkeitslehre, Wochenbl. f. Arch. u. Ing. 1883, S. 87, 96 (s.a. S. 171, 274, 299). – [6] Melan, Beitrag zur Berechnung eiserner Hallengesperre unter Anwendung des Satzes von der kleinsten Deformationsarbeit, Wochenschr. d. Oesterr. Ing.- u. Arch.-Ver. 1883, S. 149, 162. – [7] Ders., Ueber den Einfluß der Wärme auf elastische Systeme, ebend., S. 183, 202. – [8] Müller-Breslau, Beiträge zur Theorie der Versteifung labiler und flexibler Bogenträger, Zeitschr. f. Bauwesen 1883, S. 311. – [9] Melan, Beitrag zur Berechnung statisch unbestimmter Stabsysteme, Zeitschr. d. Oesterr. Ing.- u. Arch.-Ver. 1884, S. 100. – [10] Winkler, Berechnung der Windverstrebungen in Brücken mit zwei Trägern, Civilingenieur 1884, S. 111. – [11] Müller, Breslau, Der Satz von der Abgeleiteten der ideellen Formänderungsarbeit, Zeitschr. d. Arch.- u. Ing.-Vereins zu Hannover 1884, S. 211. – [12] Krohn, Das Prinzip der kleinsten Deformationsarbeit, Zeitschr. d. Ver. deutsch. Ing. 1884, S. 320 (s.a. Müller-Breslau, S. 577). – [13] Fränkel, Das Prinzip der kleinsten Deformationsarbeit der inneren Kräfte elastischer Systeme, ebend. S. 513 (s. dagegen Weyrauch, Zeitschr. f. Baukunde 1884, S. 452). – [14] Weyrauch, Arbeitsbedingungen für statisch unbestimmte Systeme, Wochenschr. f. Arch. u. Ing. 1884, S. 290. – [15] Müller-Breslau, Bedingungsgleichungen für statisch unbestimmte Körper, Berechnung der Formänderungen, Wochenbl. f. Arch. u. Ing. 1884, S. 373, 383. – [16] Ders., Ueber kontinuierliche Bogen und Balken, ebend., S. 463, 470, 481, 490. – [17] Ders., Die Sätze von der Formänderungsarbeit und ihre Bedeutung für die Festigkeitslehre, Zeitschr. d. Ver. deutsch. Ing. 1884, S. 577. – [18] Weyrauch, Theorie elastischer Körper, Leipzig 1884, S. 108, 153, 185, 222. – [19] Ders., Aufgaben zur Theorie elastischer Körper, Leipzig 1885, Aufgaben 35–42, 82–89, 94, 98–106. – [20] Landsberg, Ebene Fachwerke mit -festen Knotenpunkten und das Prinzip der Deformationsarbeit, Zentralbl. d. Bauverw. 1885, S. 165. – [21] Mohr, Beitrag zur Theorie des Fachwerks, Civilingenieur 1885, S. 289. – [22] Ders., Ueber die Elastizität der Deformationsarbeit, ebend. 1886, S. 395 (s.a. Müller-Breslau, S. 553). – [23] Engesser, Ueber statisch unbestimmte Träger bei beliebigem Formänderungsgesetz und über den Satz von der kleinsten Ergänzungsarbeit, Zeitschr. f. Architektur und Ingenieurwesen 1889, S. 733. – [24] Foeppl, Vorlesungen über technische Mechanik, III, Leipzig 1900, S. 176; V, Leipzig 1907, S. 259. – [25] Müller-Breslau, Die graphische Statik der Baukonstruktionen, II, 1, Leipzig 1903, S. 9, 13, 17, 30, 38, 45, 49; II, 2, Leipzig 1908, S. 107, 309, 341. – [26] Ders., Die neueren Methoden der Festigkeitslehre, Leipzig 1904, S. 22, 58, 72, 77, 227, 235, 245, 306, 329. – [27] Ostenfeld, Technische Statik, Leipzig 1904, S. 213, 378. – [28] Mehrtens, Vorlesungen über Statik der Baukonstruktionen und Festigkeitslehre, III, Leipzig 1905, S. 1, 64, 215 u.s.w. – [29] Bach, Elastizität und Fertigkeit, Berlin 1905, S. 381. – [30] Kriemter, Von der Erhaltung der Energie und dem Gleichgewicht des nachgiebigen Körpers, Zeitschr. f. Architektur und Ingenieurwesen 1905, S. 311 (s.a. 1908, S. 17). – [31] Mohr, Abhandlungen aus dem Gebiete der technischen Mechanik, Berlin 1906, S. 343. – [32] Engesser, Ueber die Berechnung statisch unbestimmter Systeme, Zentralbl. d. Bauverw. 1907, S. 606. – [33] Keck-Hotop, Vorträge über Elastizitätslehre, II, Leipzig 1908, S. 8, 333. – [34] Weyrauch, Ueber statisch unbestimmte Fachwerke und den Begriff der Deformationsarbeit, Zeitschr. f. Architektur u. Ingenieurwesen 1908, S. 91. – S.a. Biegungsarbeit, Torsionsarbeit, Clapeyrons Theorem, Fachwerke, statisch unbestimmte (Bd. 3, S. 551), Träger, zusammengesetzte, Gegenseitigkeit der Verrückungen, Potential, elastisches, Proportionale Widerstände.
Weyrauch.
http://www.zeno.org/Lueger-1904.