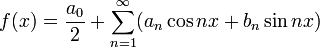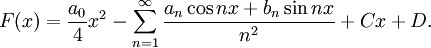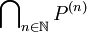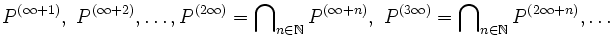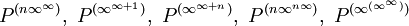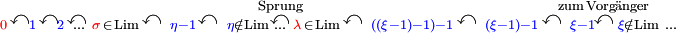- Ordinalzahlen
-
Beim Zählen benutzt man Ordinalzahlen (auch Ordnungszahlen genannt), um die Position eines Elements in einer Folge anzugeben: „Erstes, zweites, drittes, … Element“. Sprachlich benutzt man dazu bestimmte Zahlwörter. Auf diese Weise ordnet man jedem Element der Folge eine natürliche Zahl zu, die zum Index dieses Elementes wird. Mit Hilfe der Indizes kann man feststellen, ob ein Element vor einem anderen Element steht, wie „weit“ es vom Anfang der Folge entfernt ist und - falls es einen Vorgänger hat - diesen Vorgänger bestimmen. Solche Schlussfolgerungen kann man nicht nur für die Folge insgesamt treffen, sondern auch für jede ihrer Teilfolgen, die genau so wie die gesamte Folge ein Anfangselement und Nachfolgeelemente besitzen.
Eine natürliche Zahl kann für zwei Zwecke benutzt werden: Zum einen, um die Anzahl der Elemente einer (endlichen) Menge zu beschreiben, und zum anderen, um die Position eines Elements in einer geordneten Menge anzugeben. Georg Cantor hatte die Idee, wie man diese Konzepte innerhalb der Mengenlehre auf unendliche Mengen verallgemeinern kann. Während die beiden Konzepte – Zahl als Messinstrument für Größe und Zahl als Index – für endliche Mengen übereinstimmen, muss man sie für unendliche Mengen unterscheiden.
Die Beschreibung der Größe einer Menge führt zu dem Begriff Kardinalzahl, während die Beschreibung der Position in einer geordneten Menge zu dem Begriff Ordinalzahl führt, wie er in diesem Artikel beschrieben wird. Die Gesamtheit der Ordinalzahlen, die man meistens mit On oder Ord bezeichnet, bildet in der modernen Mengenlehre – genauso wie die Gesamtheit der Kardinalzahlen – eine echte Klasse.
Inhaltsverzeichnis
Geschichte der Entdeckung
Dass es einer Erweiterung des Systems der natürlichen Zahlen bedarf, ist von Cantor festgestellt worden, als er die Frage untersucht hat, welche von den reellen Funktionen eine eindeutige Darstellung durch trigonometrische Reihen haben. Ihm war aus Vorarbeiten von E. Heine bekannt, dass die im Intervall ( − π,π) stetigen Funktionen eine solche Darstellung haben. Cantor zeigte (1870), dass dies für jede Funktion richtig ist, deren trigonometrische Reihe überall konvergiert. Die Frage nach der Existenz von weiteren Funktionenklassen, die diese Eigenschaft besitzen, ist damit aber noch nicht beantwortet. Schon der Satz von Heine ist für Funktionen richtig, die fast überall stetig sind, also solche mit einer endlichen Menge E von Unstetigkeitsstellen. Die Frage nach der Eindeutigkeit ist äquivalent zu der Frage, ob das Verschwinden der trigonometrischen Reihe
auf der Menge ( − π,π) \ E auch das Verschwinden der Koeffizienten {an}n = 0,1,... und {bn}n = 1,2,... nach sich zieht. Mengen E mit dieser Eigenschaft werden Mengen vom Typ U genannt (aus dem französischen unicité – Eindeutigkeit) und alle anderen Mengen – Mengen vom Typ M (multiplicité – Mehrdeutigkeit).[1] Endliche Mengen sind also Mengen vom Typ U. Indem man f(x) zweimal integriert, erhält man die Riemann-Funktion:[2]
Wenn F(x) linear ist, dann sind alle {an}n = 0,1,... und {bn}n = 1,2,... gleich 0. Wenn man also für eine Menge P beweisen würde, dass aus
 x
x  (( − π,π) \ P) (f(x) = 0) die Linearität von F(x) folgt, dann wäre damit auch die Zugehörigkeit von P zum Typ U bewiesen worden. Cantor verwendet diese Idee in seinem Artikel „Über die Ausdehnung eines Satzes aus der Theorie der trigonometrischen Reihen“[3] vom Jahre 1871 und zeigt:
(( − π,π) \ P) (f(x) = 0) die Linearität von F(x) folgt, dann wäre damit auch die Zugehörigkeit von P zum Typ U bewiesen worden. Cantor verwendet diese Idee in seinem Artikel „Über die Ausdehnung eines Satzes aus der Theorie der trigonometrischen Reihen“[3] vom Jahre 1871 und zeigt:- „Ist (p,q) irgendein Intervall, in der nur eine endliche Anzahl von Punkten der Menge P liegt, so ist F(x) in diesem Intervalle linear …“ (dort Seite 131)
Falls P unendlich ist, dann hat sie mindestens einen Häufungspunkt. Cantor nennt die Menge der Häufungspunkte einer Menge P abgeleitete Menge und bezeichnet sie mit P(1), die abgeleitete von P(1) bezeichnet er mit P(2) usw. (siehe Hauptartikel: Ableitung einer Menge). Falls nach endlich vielen Schritten eine endliche Menge P(n) erreicht wird, dann nennt Cantor die Menge P eine Menge n-ter Art. Cantor stellt fest, dass sich die Linearität von F(x) in dem Intervall (p,q) auch dann beweisen lässt, wenn (p,q) endlich viele Punkte der Menge P(k) enthält, wobei die Korrektheit dieser Aussage von der Wahl der natürlichen Zahl k nicht abhängig ist. Mengen mit einer leeren mehrfachen Ableitung sind also immer vom Typ U.
In diesem Artikel gehen die Cantorschen Überlegungen noch nicht über endliche Iterationsprozesse hinaus; allerdings enthält er schon Denkmuster, die später die gesamte Mengenlehre prägen werden. Er ordnet der Veranschaulichung der reellen Zahlen durch geometrische Punkte eine zweitrangige Rolle zu, indem er die reellen Zahlen als Cauchy-Folgen aus Elementen der Menge A der rationalen Zahlen definiert. Die Menge dieser Folgen bezeichnet er mit B und definiert dort die für A üblichen Rechenarten. Cauchy-Folgen aus Elementen der Menge B bilden eine weitere Menge C. Dieser Prozess lässt sich theoretisch ins Unendliche fortsetzen. Cantor versteht von nun an unter Punkt ein Element irgendwelcher Mengen A, B, C, … Der Aufbau solcher geordneter Hierarchien, bei denen der Übergang von einer Stufe zur Nächsten durch Grenzübergänge erfolgt, ist später zu einem häufig eingesetzten Mittel zur Einführung neuer mengentheoretischen Begriffe geworden. Wir werden sehen, dass eine solche Hierarchie auch bei den Ordnungszahlen zu erkennen ist.
Nach dieser Arbeit über trigonometrischen Reihen hat sich das Interesse Cantors für das Problem einer gleichzeitig notwendigen und hinreichenden Bedingung für die Eindeutigkeit der Entwicklung von Funktionen in trigonometrischen Reihen abgeschwächt. Die Frage ist später sehr intensiv von du Bois-Reymond, de la Vallée Poussin, Young, Denjoy, Bari, Raichmann und Menschow untersucht worden allerdings ohne dabei zu einem zufriedenstellenden Ergebnis zu kommen.[1] Cantor selbst hat sich der Aufgabe gewidmet, die Punktmengen danach zu klassifizieren, wann der Prozess des Ableitens endet. Mengen, bei denen das nach endlich vielen Schritten passiert, nennt Cantor Mengen der ersten Gattung. Eine Menge P ist genau dann eine Menge der ersten Gattung, wenn der Durchschnitt
nicht leer ist. Ein natürlicher Gedanke dabei ist, genau diese Menge zu der ersten Ableitung transfiniter Ordnung zu machen für Mengen zweiter Gattung. Cantor bezeichnet sie mit
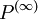 . Darauf folgen die Ableitungen
. Darauf folgen die AbleitungenCantor schreibt in seinem Artikel Über unendliche, lineare Punktmannichfaltigkeiten von 1880: [4]
- „Durch consequentes Fortschreiten gewinnt man successive die weiteren Begriffe:
- usw.; wir sehen hier eine dialektische Begriffserzeugung, welche immer weiter führt und dabei frei von jeglicher Willkür in sich nothwendig und consequent bleibt.“
In diesem nicht mal fünf Seiten langen Artikel ist der so gut wie ganze Weg gezeichnet worden, wie man aus den natürlichen Zahlen ein vollständiges transfinites System von Ordnungszahlen entwickeln kann. Den Begriff der Ordnungszahl definierte er dann als Ordnungstyp wohlgeordneter Mengen in seinen beiden Artikeln der Beiträge zur Begründung der transifiniten Mengenlehre von 1895/97.[5]
Die natürlichen Zahlen als geordnete Mengen
Die Ordinalzahlen sind in der modernen Mathematik ein Begriff der Mengenlehre. Um sie als Verallgemeinerung der natürlichen Zahlen zu definieren, ist es naheliegend die natürlichen Zahlen in eine mengentheoretische Hierarchie einzubetten.[6] Dabei erklärt man die leere Menge für die Null der natürlichen Zahlenfolge. Die leere Menge ist also die im Peano-Axiomensystem der natürlichen Zahlen speziell ausgezeichnete und nicht explizit definierte Zahl ohne Vorgänger. Nach einem Vorschlag von John von Neumann definiert man dann jede weitere Zahl als die Menge der Zahlen, die schon definiert sind:[7]
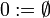
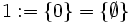

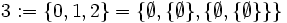

- …
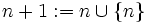
- …
Die Mengen 0, 1, 2 usw. sind durch die Elementrelation (n
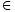 n + 1) wohlgeordnet. Zum Beispiel hat die Zahl 4 die Elemente 0, 1, 2, 3, die als 0 < 1 < 2 < 3 geordnet werden. Man schreibt deshalb auch 4: = {0 < 1 < 2 < 3}. Eine natürliche Zahl a ist also kleiner als eine Zahl b wenn a ein Element von b ist. Für die gesamte Menge der natürlichen Zahlen setzt man: ω: = {0 < 1 < 2 < 3 < ...}. Die Menge ω stellt ein Modell des Peano-Axiomensystems dar. Ihre Existenz wird in der Zermelo-Fraenkelschen Mengenlehre durch das Unendlichkeitsaxiom gesichert.
n + 1) wohlgeordnet. Zum Beispiel hat die Zahl 4 die Elemente 0, 1, 2, 3, die als 0 < 1 < 2 < 3 geordnet werden. Man schreibt deshalb auch 4: = {0 < 1 < 2 < 3}. Eine natürliche Zahl a ist also kleiner als eine Zahl b wenn a ein Element von b ist. Für die gesamte Menge der natürlichen Zahlen setzt man: ω: = {0 < 1 < 2 < 3 < ...}. Die Menge ω stellt ein Modell des Peano-Axiomensystems dar. Ihre Existenz wird in der Zermelo-Fraenkelschen Mengenlehre durch das Unendlichkeitsaxiom gesichert.Motivation und Definition
Die Theorie der Ordinalzahlen ist eine Abstraktionstheorie, bei der von der „wahren Natur“ der Mengenelemente abgesehen wird und nur solche Eigenschaften untersucht werden, die aus ihrer Anordnung abgeleitet werden können. Man definiert dazu: Eine Bijektion f: A→B von der total geordneten Menge (A, ≤A) auf die total geordneten Menge (B, ≤B) heißt Ordnungsisomorphismus (oder ähnliche Abbildung), wenn a ≤A b und f(a) ≤B f(b) für alle a,b
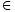 A äquivalent sind. Man sagt: die Mengen A und B sind ordnungsisomorph (oder ähnlich) und schreibt A
A äquivalent sind. Man sagt: die Mengen A und B sind ordnungsisomorph (oder ähnlich) und schreibt A 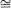 B, wenn es zwischen A und B einen Ordnungsisomorphismus gibt. Die Gesamtheit aller zueinander ordnungsisomorphen Mengen stellt eine Äquivalenzklasse dar, die Ordnungstypus genannt wird.
B, wenn es zwischen A und B einen Ordnungsisomorphismus gibt. Die Gesamtheit aller zueinander ordnungsisomorphen Mengen stellt eine Äquivalenzklasse dar, die Ordnungstypus genannt wird.Man kann zeigen, dass jede endliche wohlgeordnete Menge ordnungsisomorph zu (genau) einer natürlichen Zahl ist. Außerdem sind für eine wohlgeordnete Menge die folgenden drei Aussagen äquivalent: 1.) Sie ist endlich. 2.) Die umgekehrte Ordnung ist eine Wohlordnung. 3.) Jede nichtleere Teilmenge hat ein größtes Element.
Dies liefert die Grundlage für die Verallgemeinerung der natürlichen Zahlen zu Ordinalzahlen, die als spezielle wohlgeordnete Mengen so gewählt werden, dass jede wohlgeordnete Menge ordnungsisomorph zu genau einer Ordinalzahl ist. Somit ist jede Ordinalzahl also spezieller Repräsentant eines bestimmten Ordnungstypus. Die folgende Definition verbessert Cantors Ansatz und wurde zuerst von John von Neumann angegeben:[7]
Definition I. (setzt das Fundierungsaxiom voraus): Eine Menge S heißt Ordinalzahl, wenn jedes Element von S auch Teilmenge von S ist und S bezüglich der Mengeninklusion „
 “ total geordnet ist.
“ total geordnet ist.Eine solche Menge S ist automatisch wohlgeordnet aufgrund des Fundierungssaxioms, welches besagt: Jede nichtleere Menge S hat ein Element a, das disjunkt zu S ist. Die natürlichen Zahlen sind nach dieser Definition Ordinalzahlen. Zum Beispiel ist 2 = {0,1} ein Element von 4 = {0,1,2,3} und gleichzeitig eine Teilmenge. ω ist ebenfalls eine Ordinalzahl, die kleinste transfinite Ordinalzahl (größer als jede natürliche Zahl). Die Neumannsche Definition hat gegenüber der ersten Definition den Vorteil, dass sie aus der Sicht der Grundlagenforschung ein innerhalb der axiomatischen Mengenlehre einwandfrei definiertes mengentheoretisches Objekt bestimmt. Jede wohlgeordnete Menge X ist ordnungsisomorph zu genau einer Ordinalzahl, die man meistens mit ord(X) oder X bezeichnet.
Bemerkungen und andere Definitionen
Das Verwenden von Äquivalenzklassen aller Mengen bezüglich des Ordnungsisomorphismus gilt aus der Sicht der modernen Mathematik deshalb als problematisch, weil diese „unfassbar große Objekte“ darstellen, die im Gegensatz zu den von Neumannschen Ordinalzahlen genetisch und nicht substantiell definiert sind. Ihre Existenz wird in der naiven Mengenlehre ohne explizite Begründung angenommen und kann innerhalb von ZFC ohne Verwendung von Ordinalzahlen nicht begründet werden.[8]
In jeder Mengenlehre bezeichnet man als Ordinalzahlen solche Objekte, die das Ordinalzahlaxiom erfüllen.[9] Dieses besagt: Jeder wohlgeordneten Menge (oder gegebenenfalls anderer wohlgeordneten Struktur) kann eine Ordinalzahl so zugewiesen werden, dass beliebige an zwei verschiedenen Mengen zugewiesene Ordinalzahlen genau dann gleich sind, wenn die beiden Mengen ordnungsisomorph zueinander sind. In allen axiomatischen Mengenlehren versucht man, um die Einführung neuer Grundobjekte zu vermeiden, geeignete von der Theorie vorgegebene Objekte zu finden, die das Ordinalzahlaxiom erfüllen. Eine Möglichkeit dafür ist es spezielle Mengenhierarchien (wie die der von Neumannschen Zahlen) aufzubauen.
Mit welchen Schwierigkeiten der Verzicht auf solche Hierarchien verbunden sein kann, lässt sich am Beispiel der allgemeinen linearen Ordnungen verdeutlichen, für die man keine geeignete Mengenhierarchie kennt (2004). Das Postulieren der Existenz von Ordnungstypen kann in diesem Fall nur durch Rückgriff auf Rang- oder Stufenfunktionen vermieden werden.[10] Nachdem spezielle Objekte, die zur Einführung von Ordinalzahlen geeignet wären, schon benannt worden sind, wird das Ordinalzahlaxiom (falls überhaupt möglich) eliminiert (auf ein Theorem zurückgestuft). Innerhalb von ZFC braucht man dafür das von Fraenkel 1922 zu dem Zermeloschen Axiomensystem extra dazugefügte Ersetzungsaxiom.[11]
Wie groß die mengentheoretische Stärke des Ordinalzahlaxioms ist, deutet die Tatsache an, dass für den Beweis der Existenz „vieler“ von Neumannschen Ordinalzahlen das Unendlichkeits-, das Ersetzungs- und für manche sogar das Auswahlaxiom herangezogen werden muss.[12] Die von Neumannsche Definition der Ordinalzahlen ist die heutzutage am meisten verwendete. Aber auch in den axiomatischen Mengenlehren sind Definitionen von Ordinalzahlen zu finden, die zur Bildung von Äquivalenzklassen greifen, was aber um Antinomien zu vermeiden unter Berücksichtigung bestimmter Restriktionen passiert. So ist z. B. die Menge der abzählbaren Ordinalzahlen ω1 nach Hartogs die Menge der Äquivalenzklassen bezüglich des Ordnungsisomorphismus in der Teilmenge der wohlgeordneten Elementen von {(M,O) | M
 N; O
N; O  M×M}, wenn N = ω ist.[13] (ω1, < ) ist mit (η, < η) < (β, < β)
M×M}, wenn N = ω ist.[13] (ω1, < ) ist mit (η, < η) < (β, < β) 
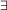 ξ
ξ  β (({x | x < βξ}, < β)
β (({x | x < βξ}, < β) 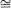 (η, < η)) wohlgeordnete Menge.[14] Diese Hierarchie lässt sich fortsetzen, indem man N = ωn setzt und die Mengen ωn + 1 für n = 1,2,... bildet. Die Definition von Hartogs verwendet keine Repräsentantenauswahl und ist ausreichend für viele Anwendungen der Ordinalzahlen in der Analysis und in der Topologie. Äquivalenzklassen von ordnungsisomorphen Mengen werden auch in den Mengenlehren mit stufentheoretischem Aufbau gebildet (Russell,[15] Quine,[16] Scott,[17] Klaua u. a.). In der AM von Klaua z. B. sind alle Mengen Elemente von Allmengen.[18] Die Ordinalzahl der wohlgeordneten Menge A ist dann die Äquivalenzklasse aller zu A ordnungsisomorphen Elemente der kleinsten Allmenge, die zu A ordnungsisomorphe Mengen enthält.[19] In der Scott-Potter-Mengenlehre, die Beispiel für Mengenlehre ohne Ersetzungsaxiom ist, werden die von Neumannschen Ordinalzahlen Pseudoordinalzahlen genannt.[20],[21] Die Ordinalzahlen in dieser Mengenlehre werden für jede wohlgeordnete Kollektion a durch ord(a) =
(η, < η)) wohlgeordnete Menge.[14] Diese Hierarchie lässt sich fortsetzen, indem man N = ωn setzt und die Mengen ωn + 1 für n = 1,2,... bildet. Die Definition von Hartogs verwendet keine Repräsentantenauswahl und ist ausreichend für viele Anwendungen der Ordinalzahlen in der Analysis und in der Topologie. Äquivalenzklassen von ordnungsisomorphen Mengen werden auch in den Mengenlehren mit stufentheoretischem Aufbau gebildet (Russell,[15] Quine,[16] Scott,[17] Klaua u. a.). In der AM von Klaua z. B. sind alle Mengen Elemente von Allmengen.[18] Die Ordinalzahl der wohlgeordneten Menge A ist dann die Äquivalenzklasse aller zu A ordnungsisomorphen Elemente der kleinsten Allmenge, die zu A ordnungsisomorphe Mengen enthält.[19] In der Scott-Potter-Mengenlehre, die Beispiel für Mengenlehre ohne Ersetzungsaxiom ist, werden die von Neumannschen Ordinalzahlen Pseudoordinalzahlen genannt.[20],[21] Die Ordinalzahlen in dieser Mengenlehre werden für jede wohlgeordnete Kollektion a durch ord(a) = 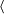 x | x
x | x 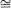 a
a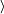 definiert[22] und die Ordinalzahlen der wohlgeordneten Mengen als kleine Ordinalzahlen bezeichnet. On ist die Kollektion der kleinen Ordinalzahlen und Ord(On) – die kleinste große Ordinalzahl. Eine Kollektion aller Ordinalzahlen gibt es in der Scott-Potter-Mengenlehre nicht.
definiert[22] und die Ordinalzahlen der wohlgeordneten Mengen als kleine Ordinalzahlen bezeichnet. On ist die Kollektion der kleinen Ordinalzahlen und Ord(On) – die kleinste große Ordinalzahl. Eine Kollektion aller Ordinalzahlen gibt es in der Scott-Potter-Mengenlehre nicht.Wie schon erwähnt kann die Wohlordnungseigenschaft der Ordinalzahlen in ZF aus dem Fundierungsaxioms abgeleitet werden. Allerdings ist es in der mengentheoretischen Literatur üblich Definitionen möglichst unabhängig von den Axiomen zu formulieren. Wir geben hier sieben weitere Definitionen der Ordinalzahlen, die alle in ZF ohne das Fundierungsaxiom zu einander und in ZF mit dem Fundierungsaxiom auch zu der oben formulierten Definition äquivalent sind.[23] Vorher zwei Begriffe: Eine Menge X heißt transitiv, wenn
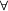 y
y  X
X 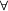 z
z  y (z
y (z  X). Eine Menge X ist genau dann transitiv, wenn
X). Eine Menge X ist genau dann transitiv, wenn 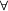 y
y  X (y
X (y  X). Eine Menge X heißt fundiert, wenn es ein y
X). Eine Menge X heißt fundiert, wenn es ein y  X gibt, so dass y und X disjunkt sind.
X gibt, so dass y und X disjunkt sind.Definition II. (Zermelo, 1915): Die Menge X heißt Ordinalzahl, wenn für jedes y
 X die Menge y
X die Menge y 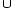 {y} entweder ein Element von X oder identisch mit X ist und für jede Teilmenge Y von X die Vereinigung der Elemente von Y entweder ein Element von X oder identisch mit X ist. [24]
{y} entweder ein Element von X oder identisch mit X ist und für jede Teilmenge Y von X die Vereinigung der Elemente von Y entweder ein Element von X oder identisch mit X ist. [24]Definition III. (von Neumann, 1923): Eine wohlgeordnete Menge X heißt Ordinalzahl, wenn
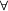 y
y  X (y = {z | z
X (y = {z | z  X; z < y}) .[25]
X; z < y}) .[25]Definition IV. (Gödel, 1937): Die transitive Menge X, deren Elemente transitiv sind, heißt Ordinalzahl, wenn jede nicht-leere Teilmenge von X fundiert ist.
Definition V. (Robinson, 1937): Die transitive Menge X, deren Elemente transitiv sind, heißt Ordinalzahl, wenn für jede zwei Elemente y und z von X entweder y
 z oder z
z oder z  y gilt.[26]
y gilt.[26]Definition VI. (Bernays, 1941): Die transitive Menge X heißt Ordinalzahl, wenn alle transitive echte Teilmengen von X Elemente von X sind.
Definition VII. Eine irreflexiv geordnete Menge (X,
 ) heißt Ordinalzahl, wenn sie transitiv und wohlgeordnet ist.
) heißt Ordinalzahl, wenn sie transitiv und wohlgeordnet ist.Definition VIII. Ordinalzahlen sind die Bilder der Funktionen E(a) = {E(x) | x < a; x
 A} für wohlgeordnete Mengen A.
A} für wohlgeordnete Mengen A.Die letzte Definition zeichnet sich durch besondere Eleganz aus, da sie auch gleich zeigt wie man die Ordinalzahl einer wohlgeordneten Menge bestimmen kann. Dass die Funktionen E(a) wohldefiniert sind, folgt aus dem Satz über die transfinite Rekursion und dass ihre Bilder – genannt Epsilonbilder – Mengen sind, aus dem Ersetzungsaxiom.
Limes- und Nachfolgerzahlen
Die Elemente einer (von Neumannschen) Ordinalzahl sind selbst Ordinalzahlen.[27] Hat man zwei Ordinalzahlen σ und τ, dann ist σ ein Element von τ genau dann, wenn σ eine echte Teilmenge von τ ist, und es gilt, dass entweder σ ein Element von τ, oder τ ein Element von σ, oder σ = τ ist.[27] Damit ist durch die Elementenbeziehung zwischen den Elementen einer Ordinalzahl eine irreflexive Totalordnungsrelation definiert. Es gilt sogar noch mehr: jede Menge von Ordinalzahlen ist wohlgeordnet.[28] Dies verallgemeinert das Wohlordnungsprinzip, dass jede Menge von natürlichen Zahlen wohlgeordnet ist, und erlaubt die freie Anwendung der transfiniten Induktion und der Beweismethode des „unendlichen Abstiegs“ auf Ordinalzahlen.
Jede Ordinalzahl σ hat genau die Ordinalzahlen als Elemente, die kleiner sind als σ. Die mengentheoretische Struktur einer Ordinalzahl ist also vollständig durch kleinere Ordinalzahlen beschrieben. Jeder Durchschnitt oder Vereinigung von Ordinalzahlen ist eine Menge von Ordinalzahlen. Weil jede Menge von Ordinalzahlen wohlgeordnet ist, ist jede transitive Menge von Ordinalzahlen selbst eine Ordinalzahl (s. Definition VII.).[27] Man folgt daraus, dass auch jeder Durchschnitt oder Vereinigung von Ordinalzahlen eine Ordinalzahl ist.[29] Die Vereinigung aller Elemente einer Menge von Ordinalzahlen S wird Supremum von S genannt und mit sup S bezeichnet. Es ist nicht schwer zu zeigen, dass β
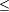 supS für jedes β
supS für jedes β S gilt und dass es zu jedem β < supS ein ξ
S gilt und dass es zu jedem β < supS ein ξ S mit β < ξ gibt. Im Sinne dieser Definition ist das Supremum der leeren Menge die leere Menge, also die Ordinalzahl 0.
S mit β < ξ gibt. Im Sinne dieser Definition ist das Supremum der leeren Menge die leere Menge, also die Ordinalzahl 0.Wohlgeordnete Mengen sind nie einer ihrer Anfangsstrecken ordnungsisomorph.[27] Deshalb existiert zwischen zwei Ordinalzahlen nur dann eine ähnliche Abbildung, wenn sie gleich sind. Die Klasse aller Ordinalzahlen ist keine Menge (s. auch: das Burali-Forti-Paradoxon). Wäre sie nämlich eine Menge, dann wäre sie eine wohlgeordnete und transitive Menge – also eine Ordinalzahl θ, für die θ
 θ gilt. Ordinalzahlen θ, die sich selbst als Element enthalten, existieren allerdings nicht,[30] weil sie ordnungsisomorph zu einer ihrer Anfangsstrecken sein müssten (nämlich zu {β | β < θ}). Aus dem Satz, dass On eine echte Klasse ist, folgt, dass für jede Menge aus Ordinalzahlen S Ordinalzahlen existieren, die größer sind als jedes Element von S. [31] Unter den Ordinalzahlen größer als jedes Element einer Menge aus Ordinalzahlen gibt es immer eine kleinste.[32] Man nennt sie obere Grenze[33],[34] der Menge S und bezeichnet sie mit sup + S.
θ gilt. Ordinalzahlen θ, die sich selbst als Element enthalten, existieren allerdings nicht,[30] weil sie ordnungsisomorph zu einer ihrer Anfangsstrecken sein müssten (nämlich zu {β | β < θ}). Aus dem Satz, dass On eine echte Klasse ist, folgt, dass für jede Menge aus Ordinalzahlen S Ordinalzahlen existieren, die größer sind als jedes Element von S. [31] Unter den Ordinalzahlen größer als jedes Element einer Menge aus Ordinalzahlen gibt es immer eine kleinste.[32] Man nennt sie obere Grenze[33],[34] der Menge S und bezeichnet sie mit sup + S.Die kleinste Ordinalzahl s(ξ) größer als die Ordinalzahl ξ heißt Nachfolger von ξ. Der Nachfolger der Ordinalzahl ξ wird oft mit ξ + 1 bezeichnet. Diese Bezeichnung ergibt somit einen Sinn auch außerhalb der transfiniten Arithmetik (ohne zu dieser in Widerspruch zu stehen). Falls ξ ein größtes Element hat, dann wird dieses Vorgänger von ξ genannt und mit ξ − 1 bezeichnet. Nicht jede Ordinalzahl hat einen Vorgänger (wie z. B. ω). Man nennt eine Ordinalzahl, die einen Vorgänger hat (wie z. B. die 1), Nachfolgerzahl oder Zahl erster Art. Eine Ordinalzahl ξ ist genau dann von erster Art, wenn ξ = s(sup ξ). Die Ordinalzahlen erster Art und die 0 nennt man isoliert. Eine positive Ordinalzahl ohne Vorgänger wird Limeszahl (oder Grenzzahl) genannt. Eine positive Ordinalzahl ξ ist genau dann Limeszahl, wenn ξ = sup ξ. Als Ordinalzahlen zweiter Art bezeichnet man die Limeszahlen sowie die 0. Jede Ordinalzahl ist somit eine Zahl entweder der ersten oder zweiten Art und entweder Limeszahl oder isoliert, wobei für positive Zahlen die Begriffe Limeszahl und Zahl zweiter Art sowie isolierte Zahl und Zahl erster Art übereinstimmen. Die Zahl 0 ist die einzige isolierte Zahl zweiter Art.[33]
Der Vorgänger von s(ξ) ist für jede Ordinalzahl ξ die Ordinalzahl ξ selbst. Die Limeszahlen bilden eine echte Klasse, die mit Lim bezeichnet wird. Falls ξ eine Ordinalzahl erster Art ist, dann existiert eine endliche aber keine unendliche Folge: ξ, ξ − 1, (ξ − 1) − 1, ((ξ − 1) − 1) − 1, ...[35] Angefangen bei ξ erreicht man nach endlich vielen Abstiegen von einer Ordinalzahl zu ihrem Vorgänger eine Zahl zweiter Art. Es gilt sogar noch mehr: Falls ξ eine transfinite Ordinalzahl ist, dann kann man zwar beliebig lange echt fallende Folgen mit erstem Element ξ bilden, aber keine unendliche solche.[35]
Unendliche Folgen von Ordinalzahlen enthalten immer unendliche nicht fallende Teilfolgen.[35]
On als rekursiver Datentyp
In der Metamathematik und ganz speziell in der Beweistheorie werden die Ordinalzahlen oft rekursiv oder axiomatisch definiert, so wie die natürlichen Zahlen durch die Peano-Axiome definiert werden.[36] Der Zweck solcher Definitionen besteht aber im Unterschied zu der Ordinalzahldefinitionen der Mengenlehre nicht darin, eine echte Klasse von Ordinalzahlen zu bestimmen sondern möglichst lange Anfangsstrecken von On zu finden, die mit aus der Sicht eines metamathematischen Programms zulässigen Mitteln definiert und untersucht werden können (s. Hauptartikel: Konstruktive Ordinalzahl). Während innerhalb der Metamathematik von Schreibfiguren die Rede ist, verwendet man in der Mengenlehre und der Rekursionstheorie den von Kleene eingeführten Begriff Ordinalzahlnotation. Für die Metamathematik sind hauptsächlich die aus der Wohlordnung folgenden sowie einige arithmetischen Eigenschaften der Ordinalzahlen von Bedeutung. Wenn man die Existenz von Nachfolger- und Limeszahlen als Grundeigenschaften betrachtet, dann lässt sich innerhalb der Theorie der rekursiven Datentypen (induktiv definierten Klassen) folgende Definition für die Klasse der Ordinalzahlen On formulieren.[37] succ und sup seien die Konstruktoren des rekursiven Datentypus Ordinalzahl, 0 – der Fundierer und
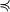 – eine Halbordnungsrelation auf On mit den Eigenschaften:
– eine Halbordnungsrelation auf On mit den Eigenschaften: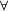 μ
μ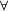 β
β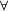 ξ(μ
ξ(μ 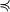 β
β 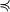 ξ
ξ 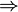 μ
μ 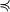 ξ)
ξ)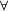 ξ(ξ
ξ(ξ 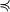 ξ)
ξ)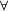 μ
μ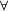 ξ(μ
ξ(μ 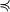 ξ
ξ 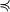 μ
μ 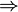 μ = ξ)
μ = ξ)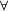 ξ(0
ξ(0 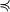 ξ)
ξ)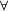 ξ(ξ
ξ(ξ 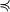 succξ)
succξ)
 ξ(ξ = succξ)
ξ(ξ = succξ)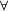 μ
μ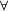 ξ(μ
ξ(μ 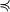 ξ
ξ 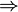 succμ
succμ 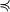 succξ)
succξ)- für jede Kette K:
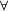 ξ(ξ
ξ(ξ K
K 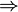 ξ
ξ 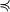 supK)
supK) - für jede Kette K:
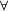 ξ(
ξ(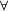 β
β K(β
K(β 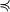 ξ)
ξ) 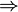 supK
supK 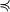 ξ)
ξ)
Man kann mittels struktureller Induktion zeigen, dass (On,
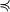 ) eine wohlgeordnete Klasse ist. In der Terminologie der Theorie der rekursiven Datentypen stellen die von Neumannschen Ordinalzahlen eine Implementierung des rekursiven Datentypus Ordinalzahl dar.
) eine wohlgeordnete Klasse ist. In der Terminologie der Theorie der rekursiven Datentypen stellen die von Neumannschen Ordinalzahlen eine Implementierung des rekursiven Datentypus Ordinalzahl dar.Rechenoperationen
- Hauptartikel: Transfinite Arithmetik
Die arithmetischen Operationen mit Ordinalzahlen werden als Verallgemeinerung der aus der elementaren Arithmetik bekannten Rechenarten eingeführt. Unter Summe zweier Ordinalzahlen η und ξ versteht man die Ordinalzahl einer wohlgeordneten Menge, die aus den Elementen der beiden Mengen besteht, wenn alle Elemente von η in der Wohlordnung vor den Elementen von ξ stehen. Dies entspricht genau die Vorstellung, die uns aus den endlichen Zahlen vertraut ist, dass beim Konkatenieren von zwei endlichen Folgen der Länge n und m eine endliche Folge der Länge m + n entsteht. Da man bei den transfiniten Ordinalzahlen zwischen isolierten und Limeszahlen unterscheiden muss, wird bei der Einführung der arithmetischen Operationen darauf geachtet, dass diese stetige Fortsetzungen der finiten arithmetischen Operationen sind. Die Stetigkeit der Rechenoperationen bei den Ordinalzahlen sieht man am deutlichsten in der sogenannten funktionalen Einführung der transfiniten Arithmetik. Die funktionale Einführung der Ordinalzahlarithmetik wird mittels transfiniter Rekursion begründet. Nicht alle aus der finiten Arithmetik bekannte Eigenschaften der Rechenoperationen sind in das Unendliche übertragbar. So ist die Addition im Allgemeinen nicht kommutativ. Mit Hilfe der Cantorschen Polynomdarstellung, die eine Art transfinites Stellenwertsystem ist, lassen sich alternative Rechenoperationen einführen: die so genannten natürlichen Operationen zwischen Ordinalzahlen, so dass keine der aus den finiten Arithmetik bekannten Regeln vermisst werden muss.
Topologische Eigenschaften
Jede Ordinalzahl lässt sich aufgrund ihrer totalen Ordnung durch die Ordnungstopologie zu einem topologischen Raum machen. In dieser Topologie konvergiert die Folge (0, 1, 2, …) gegen ω, und die Folge
- (ω, ωω, ωωω, …)
konvergiert gegen ε0. Ordinalzahlen ohne Vorgänger können stets als Grenzwert eines Netzes von kleineren Ordinalzahlen dargestellt werden. Im allgemeinen sind sie jedoch nicht Grenzwert einer Folge kleinerer Ordinalzahlen, wie z. B. die kleinste überabzählbare Ordinalzahl ω1.[38]
Die topologischen Räume ω1 und ω1+1 werden in Büchern oft als Beispiel einer nicht abzählbaren Topologie genannt. Zum Beispiel gilt im Raum ω1+1, dass das Element ω1 im Abschluss der Teilmenge ω1 liegt, aber keine Folge in ω1 gegen das Element ω1 konvergiert. Der Raum ω1 erfüllt das erste, aber nicht das zweite Abzählbarkeitsaxiom und ω1+1 keines von beiden.
Literatur
Bei Verwendung der von Neumannschen Definition:
- H. Bachmann: Transfinite Zahlen. Springer, 1967.
- O. Deiser: Einführung in die Mengenlehre. Springer, 2004, ISBN 978-3540204015.
- P. Cohen: Set Theory and the Continuum Hypothesis. W. A. Benjamin Inc., New York 1966, ISBN 978-0805323276.
- P. Komjath, V. Totik: Problems and Theorems in Classical Set Theory. Springer, 2006, ISBN 978-0387302935.
- K. Hrbacek, T. Jech: Introduction to Set Theory. Marcel Dekker Inc., New York 1999, ISBN 0-8247-7915-0.
- H. Enderton: Elements of Set Theory. Academic Press Inc., New York 1977, ISBN 978-0122384400.
- J. Barwise (Hrsg.): Handbook of Mathematical Logic. North Holland, 1977, ISBN 978-0-444-86388-1.
- A. Levy: Basic Set Theory. Springer, 1979, ISBN 3-540-08417-7.
- T. Forster: Logic, Induction and Sets. Cambridge University Press, 2003, ISBN 0-52153-361-9.
- M. Zuckerman: Sets and Transfinite Numbers. Macmillian Publishing Co., 1974, ISBN 0-02-432110-9.
- M. Deutsch: Einführung in die Grundlagen der Mathematik. Universitätsdruckerei Bremen, 1999, ISBN 3-88722-438-8.
Bei Verwendung von Ordnungstypen:
- D. Klaua: Kardinal- und Ordinalzahlen. Teil 2. Vieweg, Braunschweig 1974, ISBN 3-528-06141-3[39]
- D. Klaua: Allgemeine Mengenlehre. I., 1968 und II., 1969, Akademie Verlag Berlin.[39]
- W. Sierpinski: Cardinal and ordinal numbers. 1965, ISBN 978-0900318023.
- K. Kuratowski, A. Mostowski: Set theory. North-Holland, 1968, ISBN 978-0720404708.[40]
- M. Potter: Mengentheorie. Spektrum Akademischer Verlag, 1994, ISBN 3-86025-303-4.[39]
- E. Jacobsthal: Über den Aufbau der transfiniten Arithmetik. In: Mathematische Annalen. 66, 1909, S. 145–194
- F. Hausdorff: Grundzüge der Mengenlehre. Chelsea Publishing Company, New York 1949.
- I. P. Natanson: Theorie der Funktionen einer reellen Veränderlichen. Verlag Harri Deutsch, Frankfurt am Main 1977, ISBN 3-87144-217-8. (Auch in digitaler Form auf Russisch bei INSTITUTE OF COMPUTATIONAL MODELLING SB RAS, Krasnojarsk)
Weitere Quellen:
- K. Schütte: Proof Theory. Springer, 1977, ISBN 0-387-07911-4.
- A. Fraenkel, Y. Bar-Hillel: Foundations of set theory. North-Holland Publishing Co., 1958.
Weblinks
- Peter Hancock: Ordinals and Interactive Programs (pdf), University of Edinburgh, 2000
Einzelnachweise und Anmerkungen
- ↑ a b S. Natanson, 1977, Kapitel X., § 6.
- ↑ S. Riemann Function (bei MathWorld).
- ↑ in: Mathematische Annalen 5 (1872) S.123-132
- ↑ 2. Artikel in: Mathematische Annalen 17 (1880) 357f
- ↑ in: Mathematische Annalen 46 (1895) Seite 499 und Mathematische Annalen 49 (1897) Seite 207
- ↑ Was auch für die Mathematik insgesamt deshalb von Vorteil ist, weil dadurch zahlreiche weitere mathematische Begriffe eine mengentheoretische Interpretation erhalten.
- ↑ a b 15. August 1923 – Brief von Johann von Neumann an Ernst Zermelo (s. H. Meschkowski: Problemgeschichte der neueren Mathematik. B.I.-Wissenschaftsverlag, 1978, ISBN 3-411-01542-X. XIV.1. sowie Tafel 10.)
- ↑ Genauer: nicht ohne Verwendung des sogenannten Zurückschneidens durch Rangbetrachtung von Tarski, das aber seinerseits das Vorhandensein schon definierter Ordinalzahlen voraussetzt (s. Levy, 1979, II.7.7, II.7.13).
- ↑ s. Bachmann, 1968, § 3.5
- ↑ Für nicht fundierte Mengenuniversen muss eine solche Funktion nicht unbedingt vorhanden sein.
- ↑ A. Fraenkel: Zu den Grundlagen der Cantor-Zermeloschen Mengenlehre. In: Mathematische Annalen. 86, 1922, S. 230–237
- ↑ s. Deiser, 2004, 2.6., S. 256 u. 3.1, S. 433 sowie Bachmann, 1968, § 6., § 38., § 42.
- ↑ s. O. Deiser: Reelle Zahlen. Das klassische Kontinuum und die natürlichen Folgen. Springer, 2007, ISBN 978-3540453871, S. 382–386
- ↑ Für den Beweis, dass ω1 eine Menge und keine echte Klasse ist, braucht man innerhalb von ZFC das Ersetzungsaxiom (s. Zuckerman, 1974, 5.12)
- ↑ Über die Ordinalzahlen im Sinne von Russell und Whitehead s.: J. Rosser: Logic for mathematicians. McGraw-Hill Book Company, 1953, ISBN 0-82840-294-9, XII.
- ↑ W. Quine: New Foundations for Mathematical Logic. In: American Mathematical Monthly. 44, 1937, S. 70–80
- ↑ D. Scott: Axiomatizing Set Theory. In: Proceedings of Symposia in Pure Mathematics. 13, 2, American Mathematical Society, 1971, S. 207–214
- ↑ AM: Allgemeine Mengenlehre – s. Klaua, 1968 u. Klaua, 1969
- ↑ s. Klaua, 1974 sowie D. Klaua: Eine axiomatische Mengenlehre mit größtem Universum und Hyperklassen. In: Monatshefte für Mathematik. 92, 3, 1981, S. 179–195.
- ↑ s. Potter, 1994, 6.2
- ↑ Die Pseudoordinalzahlen sind zwar vor 1923 Zermelo und Mirimanoff bekannt gewesen. Sie haben aber innerhalb von ZFC an Bedeutung gewonnen, erst nachdem von Neumann erkannt hat, dass aus dem Ersetzungsaxiom die Existenz einer Rangfunktion für alle Mengen und einer Ordinalzahlfunktion für alle wohlgeordnete Mengen folgt. Deshalb sind heutzutage die Pseudoordinalzahlen vor allem durch den Begriff von Neumannsche Zahlen bekannt.
- ↑ Hier ist
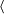 x | Φ(x)
x | Φ(x) 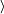 = {x | Φ(x)
= {x | Φ(x) 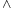
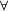 y(Φ(y)
y(Φ(y) 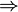 D(x)
D(x) D(y))}, wobei D(a) das bezüglich der
D(y))}, wobei D(a) das bezüglich der 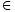 -Relation kleinste Element von {b | a
-Relation kleinste Element von {b | a 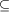 b
b 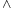 T(b)} ist und T(a): =
T(b)} ist und T(a): =  d(H(d)
d(H(d) 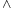 a = acc(d)), H(a): = (
a = acc(d)), H(a): = ( d
d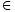 a)(d = acc(d
a)(d = acc(d  a)), acc(a): = {x | x
a)), acc(a): = {x | x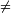 {y | y
{y | y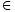 x}
x} (
(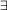 b
b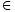 a)(x
a)(x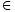 b
b x
x 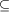 b)}.
b)}. - ↑ s. Bachmann, 1967, § 4.3 sowie Deiser, 2004, 2.6, S. 257–258 und Enderton, 1977, Chapter 7., S. 182–194
- ↑ Diese unveröffentlichte Definition von Zermelo aus dem Jahr 1915 referiert Paul Bernays, sein damaliger Mitarbeiter in Zürich: Bernays, A System of Axiomatic Set Theory II, in: Journal of Symbolic Logic 6 (1941), S. 6 und 10. Bemerkung: Für die leere Teilmenge ergibt die letzte Bedingung, dass die Ordinalzahl die leere Menge enthält oder leer ist, was Bernays zusätzlich fordert. Durch Verschärfung von Zermelos 'oder' zu 'entweder-oder' kann auf das Fundierungsaxiom verzichtet werden.
- ↑ s. auch J. v. Neumann: Die Axiomatisierung der Mengenlehre. In: Mathematische Zeitschrift. 27, 1., 1928, S. 669–752, V.1.
- ↑ s. auch Fraenkel, Bar-Hillel, 1958, II., §7.
- ↑ a b c d s. Levy, 1979, II.2.14, II.3.11, II.3.12, II.3.13, II.3.16
- ↑ Eine Wohlordnungsrelation lässt sich auch zwischen Wohlordnungstypen definieren (zwischen Ordnungzahlen im Sinne von Cantor also). Eine wohlgeordnete Menge S heißt kleiner (oder kürzer) als eine wohlgeordnete Menge T, wenn S ordnungsisomorph zu einer echten Untermenge von T ist. Es sei die Vereinbarung getroffen, dass im weiteren, wenn nicht ausdrücklich etwas anderes gesagt ist, unter Ordinalzahl eine Ordinalzahl im von Neumannschen Sinne gemeint sein wird und dass die Behauptungen, die aufgestellt werden, Sätze in ZF oder ZFC sind.
- ↑ Man beachte, dass Vereinigung (Durchschnitt) von Elementen einer Menge von transitiven Mengen transitiv ist.
- ↑ Diese Behauptung ist von dem Fundierungsaxiom unabhängig.
- ↑ Gäbe es nämlich solche Zahlen nicht, dann wäre On Untermenge von sup S (eine echte Menge also).
- ↑ Wenn β eine Ordinalzahl ist, die größer ist als alle Elemente der Menge S, dann ist {γ | γ
 β}\S keine echte Klasse sondern eine wohlgeordnete Menge und hat daher ein kleinstes Element.
β}\S keine echte Klasse sondern eine wohlgeordnete Menge und hat daher ein kleinstes Element. - ↑ a b s. Bachmann, 1967, § 4.1.3., § 4.1.4
- ↑ Der englische Begriff dafür ist strict upper bound.
- ↑ a b c s. Komjath, Tototik, 2006, 8.2, 8.3, 8.18
- ↑ s. zum Beispiel Schütte, 1997 und Deutsch, 1999, S. 308-309
- ↑ s. Forster, 2003, 7.1; vgl. auch mit I. Phillips: Recursion Theory. In: S. Abramsky, D. Gabbay, T. Maibaum (Hrsg.): Handbook of Logic in Computer Science. Vol. 1, Oxford University Press, 1992, ISBN 0-19853-735-2 sowie S. Cook, Hao Wang, Characterizations of Ordinal Numbers in Set Theory. Mathematische Annalen, 164, 1, 1966
- ↑ Dies lässt sich allerdings ohne das Auswahlaxiom nicht beweisen.
- ↑ a b c Diesem Buch liegt ein spezielles Axiomensystem zugrunde.
- ↑ In diesem Buch wird nirgendwo das Fundierungsaxiom verwendet.
Wikimedia Foundation.