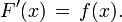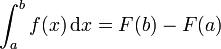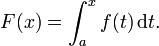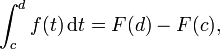- Aufleitung
-
Als Stammfunktion oder unbestimmtes Integral einer reellen Funktion f bezeichnet man eine differenzierbare Funktion F, deren Ableitungsfunktion F' mit f übereinstimmt. Ist also f auf einem Intervall I definiert, so muss F auf I definiert und differenzierbar sein, und es muss für beliebige Werte x aus I gelten:
Eine auf einem Intervall I definierte Funktion f hat unendlich viele Stammfunktionen. Ist nämlich F eine Stammfunktion von f, so ist für jede beliebige reelle Zahl C auch die durch G(x) = F(x) + C definierte Funktion G eine Stammfunktion von f. Die Bezeichnung unbestimmtes Integral bezeichnet manchmal auch die Menge aller dieser Funktionen. Ist der Definitionsbereich von f kein Intervall, so ist die Differenz zweier Stammfunktionen von f nicht notwendigerweise konstant, aber lokal konstant.
Ist f eine auf dem kompakten, also endlichen und abgeschlossenen Intervall [a, b] stetige Funktion, so lässt sich mit Hilfe einer beliebigen Stammfunktion F von f das bestimmte Integral von f über [a, b] berechnen:
Stammfunktionen werden daher für verschiedene Berechnungen benötigt, z. B.:
- Flächenberechnung für Flächen, die von Funktionsgraphen begrenzt werden
- Volumenberechnung für Rotationskörper
Für das Differenzieren gibt es einfache Regeln. Dagegen ist die Situation beim unbestimmten Integrieren ganz anders, da die Operation des unbestimmten Integierens zu einer Erweiterung vorgegebener Funktionensklassen führt, z. B. ist das Integrieren innerhalb der Klasse der rationalen Funktionen nicht abgeschlossen und führt auf die Funktionen ln und arctan. Auch die Klasse der so genannten elementaren Funktionen ist nicht abgeschlossen. So hat Joseph Liouville bewiesen, dass die einfache Funktion
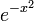 keine elementare Stammfunktion besitzt. Auch die einfache Funktion
keine elementare Stammfunktion besitzt. Auch die einfache Funktion 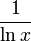 besitzt keine elementare Stammfunktion. Dagegen ist
besitzt keine elementare Stammfunktion. Dagegen ist 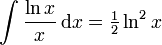 . Die Technik des Integrierens basiert auf folgenden Integrationsregeln:
. Die Technik des Integrierens basiert auf folgenden Integrationsregeln:- Additivität
- der Tabelle der sog. Grundintegrale (Übersicht über die wichtigsten Funktionen und deren Stammfunktionen).
- Methode der partiellen Integration
- Substitutionsregel
- speziellen Verfahren
- Ausnutzung raffinierter Zerlegungen und Umformungen (z. B. Polynomdivision, Partialbruchzerlegung, Funktionalgleichungen)
Da es keine allgemeine Regel zur Bestimmung von Stammfunktionen gibt, werden Stammfunktionen in sogenannten Integraltafeln tabelliert. Computeralgebrasysteme sind heute in der Lage fast alle bisher tabellierten Integrale zu berechnen.
Für jede integrierbare Funktion
![f: \, [a,b] \to \mathbb{R}](/pictures/dewiki/49/1cafc0dbd4efc686521a2440d0f15e84.png) ist eine Integralfunktion F definiert durch
ist eine Integralfunktion F definiert durchDiese Funktion ist stetig, und falls auch f stetig ist, ist F nach dem Hauptsatz der Differential- und Integralrechnung eine Stammfunktion von f. Ist jedoch f auf [a,b] integrierbar, aber nicht überall stetig, dann gilt zwar für alle c,d aus [a,b]
aber F ist in diesem Falle nicht überall differenzierbar und somit keine Stammfunktion von f.
Das oft von Schülern gebrauchte Wort Aufleitung ist kein mathematischer Fachterminus und ist auch etymologisch in Bezug auf den Begriff Ableitung nicht zu rechtfertigen. Es ist mathematisch nicht korrekt, das Finden einer Stammfunktion als bloße Umkehrung des Ableitens zu betrachten. Der genaue Zusammenhang kann nicht kürzer als im Hauptsatz formuliert werden.
Stammfunktionen für komplexwertige Funktionen
Der Begriff der Stammfunktion lässt sich auch für komplexe Funktionen formulieren. Hier reicht es jedoch nicht mehr aus, dass die Funktion f stetig ist, sie muss zudem auf einem Gebiet D, d.h. einer offenen, einfach zusammenhängenden Teilmenge des Grundraumes (in diesem Fall
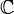 ) definiert sein. Ist diese Forderung erfüllt, gelten folgende äquivalente Aussagen:
) definiert sein. Ist diese Forderung erfüllt, gelten folgende äquivalente Aussagen:- Die Funktion f hat eine Stammfunktion auf ganz D.
- Wegintegrale über f hängen nur von den Endpunkten des Weges ab.
- Wegintegrale über geschlossene Wege (Anfangspunkt = Endpunkt) liefern als Ergebnis immer 0.
Siehe auch
Weblinks
- The Integrator – Berechnung von Stammfunktionen online
- Applet zur Integralfunktion – interaktives Arbeitsblatt mit Lösungen zur Visualisierung des Begriffs der Integralfunktion
Wikimedia Foundation.