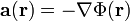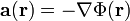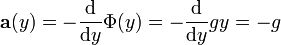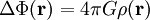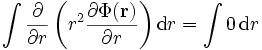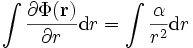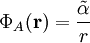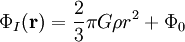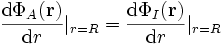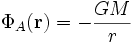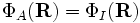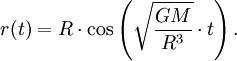- Potentialdifferenz
-
Das Potential oder auch Potenzial (lat.: potentialis, von potentia Macht, Kraft, Leistung) ist in der Physik die Fähigkeit eines konservativen Kraftfeldes, eine Arbeit zu verrichten. Es beschreibt die Wirkung eines konservativen Feldes auf Massen oder Ladungen unabhängig von diesen selbst.
Inhaltsverzeichnis
Grundlage: Das Kraftfeld
Nach Newton gilt für eine Kraft F die Beziehung
- F = ma,
wobei m eine Masse und a die Beschleunigung ist, welche diese Masse erfährt. Es handelt sich also um eine Kraft, welche auf einen einzelnen Gegenstand ausgeübt wird.
Bei der Schwerkraft wirkt jedoch an jedem Punkt im Raum eine Beschleunigung (nach unten) und eine Masse, welche sich irgendwo im Raum befindet, erfährt damit eine Kraft in diese Richtung. Eine solche Größe, welche sich nicht nur an einem einzelnen Ort befindet, sondern über einen Raum verteilt ist, nennt man ein Feld.
Eine Zahl wird auch als Skalar bezeichnet und alle Felder, welche Orten im Raum eine Zahl zuordnen, heißen skalare Felder. Beispielsweise könnte man jedem Punkt auf einer Landkarte seine Höhe über dem Meeresspiegel zuordnen und hätte damit ein skalares Feld – ein Höhenfeld.
Kräfte sind Vektoren, also gerichtete Größen. Wenn jedem Punkt im Raum ein Vektor anstatt einer Zahl angehaftet wird, so handelt es sich um ein Vektorfeld. Im Falle der Schwerkraft zeigen etwa alle Vektoren in Richtung des Erdmittelpunkts. Felder, deren Elemente Kräfte sind, heißen Kraftfelder.
Die obige Gleichung kann auch vektoriell geschrieben werden, mit
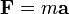 ,
,
wobei
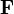 das Kraftfeld und
das Kraftfeld und 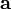 das Beschleunigungsfeld ist. Ein Beschleunigungsfeld hängt in der Regel von der Position
das Beschleunigungsfeld ist. Ein Beschleunigungsfeld hängt in der Regel von der Position 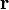 im Raum ab. Das bedeutet, dass sowohl
im Raum ab. Das bedeutet, dass sowohl 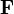 als auch
als auch 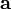 Funktionen von
Funktionen von 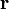 sind, also
sind, also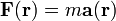 .
.
Folgerung: Das Potentialfeld
Das Beschleunigungsfeld
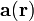 lässt sich mithilfe eines skalaren Feldes
lässt sich mithilfe eines skalaren Feldes 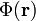 ausdrücken, wenn es sich um eine konservative Kraft, wie etwa die Schwerkraft, handelt.
ausdrücken, wenn es sich um eine konservative Kraft, wie etwa die Schwerkraft, handelt.Ein skalares Feld Φ, welches diese Beziehung erfüllt, heißt Potential des Feldes
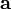 . Der Ausdruck
. Der Ausdruck 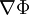 bezeichnet den Gradient des Feldes Φ. Der Gradient eines Skalarfeldes erzeugt 1. ein Vektorfeld und macht 2. eine Aussage über die Änderungsrate des Skalarfeldes in Richtung seines steilsten Anstiegs.
bezeichnet den Gradient des Feldes Φ. Der Gradient eines Skalarfeldes erzeugt 1. ein Vektorfeld und macht 2. eine Aussage über die Änderungsrate des Skalarfeldes in Richtung seines steilsten Anstiegs.Das Potential lässt sich damit gut veranschaulichen als eine hügelige Landschaft, also wie das zuvor erwähnte Höhenfeld (Potentialfeld). Die Höhe eines Punkts ist sein Potentialwert und die Kraft, welche auf einen Körper wirkt, ist derjenige Vektor, welcher in Richtung des steilsten Gefälles zeigt (also entgegen der Richtung des steilsten Anstiegs).
Die Kraft auf eine Masse im Gravitationsfeld ergibt sich zu
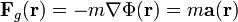 .
.
Die besondere Bedeutung des Potentials liegt darin, dass es viele Berechnungen vereinfacht. Es hat als skalares Feld nur eine Komponente im Vergleich zu den drei Komponenten des Kraftfeldes. Außerdem beschreibt es die potentielle Energie eines Probekörpers.Im allgemeineren Sinne werden auch andere skalare Felder, aus denen sich ein Vektorfeld gemäß oben stehender Gleichung ableiten lassen, als Potential bezeichnet. Das bekannteste Beispiel ist das elektrische Potential der Elektrostatik.
Vorzeichen
Das Minuszeichen in
drückt aus, dass die Beschleunigung in die Richtung wirkt, die der Richtung des maximalen Potentialanstiegs entgegengesetzt ist. Im anschaulichen Bild eines Potentialgebirges wirkt die Beschleunigung also bergab. Ein konkretes Beispiel für die Anwendung dieses Zusammenhangs veranschaulicht den Sinn dieses Vorzeichens ebenfalls: In der Nähe der Erdoberfläche ist das Potential eines Körpers in einer Höhe h=y unter der Erdbeschleunigung g > 0 näherungsweise Φ(y) = gy. Da Koordinatensysteme auf der Erdoberfläche nach oben positiv gezählt werden (denn einen Körper höher zu heben, heißt auch größeres Potential), muss die nach unten gerichtete Erdbeschleunigung negativ sein. Berechnet man anschließend das Beschleunigungsfeld, erhält man:
Die Kraft wirkt also wie erwartet in Richtung Erdmittelpunkt.
Berechnung
Das Potential eines konservativen Kraftfeldes ergibt sich durch Lösung der Poisson-Gleichung, einer partiellen Differentialgleichung zweiter Ordnung.
In der Elektrostatik lautet sie
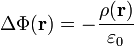 ,
,
wohingegen sie in der klassischen Gravitationstheorie die Form
besitzt. Hierbei sind Δ der Laplace-Operator und
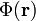 das Potential. Weiter ist
das Potential. Weiter ist 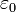 die Permittivität, G die Gravitationskonstante und
die Permittivität, G die Gravitationskonstante und 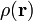 die Ladungs- bzw. Massendichte.
die Ladungs- bzw. Massendichte.Potentielle Energie und Potential
Potentielle Energie und Potential unterscheiden sich darin, dass potentielle Energie sich beispielsweise im Gravitationsfeld auf eine Masse und im elektrischen Feld auf eine Ladung bezieht und von der Größe dieser Masse oder Ladung abhängt, während das Potential eine Eigenschaft des Kraftfelds unabhängig von einer Massen- oder Ladungsgröße beschreibt.
- Das Potential ist eine dem Kraftfeld äquivalente Felddarstellung.
Der oben erwähnte Zusammenhang ermöglicht es, ein im Allgemeinen dreidimensionales Kraft-Vektorfeld mit Hilfe von skalaren Feldern darzustellen, ohne dass dabei Informationen über das Feld verloren gehen. Das führt zur Vereinfachung vieler Rechnungen. Allerdings ist der Rückschluss auf den das Feld verursachenden Körper nicht mehr eindeutig. So ist etwa das äußere Gravitationspotential einer homogenen Vollkugel dem Potential einer Punktmasse äquivalent.
Verbunden sind die beiden Größen über den Begriff der Arbeit:
- Die Energie ist aus physikalischer Sicht die Fähigkeit eines Körpers, Arbeit zu verrichten.
- Das Potential dient zur Beschreibung der Fähigkeit eines Feldes, einen Körper Arbeit verrichten zu lassen.
Der Zusammenhang zwischen potentieller Energie
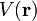 und dem Potential
und dem Potential 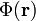 lautet
lautet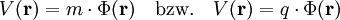 .
.
Der erste Ausdruck bezieht sich auf ein Gravitationsfeld (Masse m), der zweite auf ein elektrisches Feld (Ladung q).
Potentialdifferenz
Von Potentialdifferenz beziehungsweise Potentialunterschied spricht man immer dann, wenn zwei oder mehrere Objekte zueinander unterschiedliche Potentiale besitzen. Eine Potentialdifferenz ist also ein körperunabhängiges Maß für die Stärke eines Feldes und beschreibt das Arbeitsvermögen eines Objektes in diesem. Entlang von Äquipotentialflächen (Flächen gleichen Potentials) herrscht somit keine Potentialdifferenz. Objekte (Körper, Ladungen) können entlang dieser ohne Arbeitsaufwand verschoben werden. In der Elektrostatik ist die Potentialdifferenz definiert als elektrische Spannung zwischen zwei isolierten Ladungsträgern (Objekten unterschiedlichen Potentials).
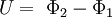 .
.
Beispiel: Gravitationspotential einer homogenen Kugel
Da das Lösen der Poisson-Gleichung bereits in einfachen Fällen relativ aufwändig ist, soll hier ein ausführliches Beispiel vorgeführt werden. Dazu betrachten wir einen idealisierten Himmelskörper als perfekte Kugel mit homogener Dichte ρ und einem Radius R.
Äußere Lösung
Im Außenraum um die Kugel herum ist r > R und ρ = 0, so dass die Poisson-Gleichung in die Laplace-Gleichung übergeht
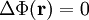 .
.
Da das gegebene Problem eine Kugelsymmetrie besitzt, können wir es vereinfachen, indem wir es in Kugelkoordinaten betrachten. Dazu muss lediglich der entsprechende Laplace-Operator in die Gleichung eingesetzt werden. Diese hat dann die Form
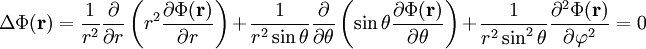 .
.
Das Feld kann aber offensichtlich nicht von den Winkeln
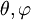 abhängen, da die Kugel symmetrisch ist. Das bedeutet, dass die Ableitungen von
abhängen, da die Kugel symmetrisch ist. Das bedeutet, dass die Ableitungen von 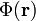 nach den Winkelkoordinaten verschwinden und nur der radiale Teil übrig bleibt.
nach den Winkelkoordinaten verschwinden und nur der radiale Teil übrig bleibt.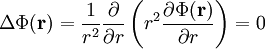 ,
,
die sich durch beidseitiges Multiplizieren mit r2 weiter vereinfacht.
Integration nach r liefert
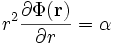 ,
,
wobei α eine Integrationskonstante ist. Weitere Integration nach r liefert
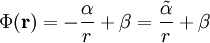 ,
,
wobei
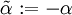 , damit das Minuszeichen verschwindet und β wieder eine Integrationskonstante ist.
, damit das Minuszeichen verschwindet und β wieder eine Integrationskonstante ist.Da das Potential in unendlicher Entfernung gegen Null gehen sollte, muss β = 0 sein. Für die äußere Lösung gilt also zunächst
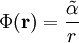 .
.
Um die Konstante zu berechnen, müssen wir jedoch zuerst die innere Lösung bestimmen.
Innere Lösung
Im Innern der Kugel ist r < R und
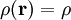 , so dass die Poisson-Gleichung gilt, mit
, so dass die Poisson-Gleichung gilt, mit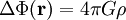 .
.
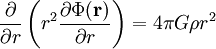 .
.
Zweimalige Integration nach r liefert auf dieselbe Weise wie zuvor
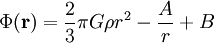 ,
,
wobei hier A,B wieder Integrationskonstanten sind. Da das Potential im Mittelpunkt der Kugel (r=0) einen endlichen Wert Φ0 annehmen sollte, muss A=0 sein. Andernfalls würde das Potential unendlich groß. Wir haben also
- Φ(0) = Φ0 = B.
und somit
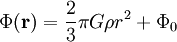 .
.
Bestimmung der Konstanten
Wir unterscheiden zunächst
für die äußere Lösung und
für die innere Lösung. Am Rand der Kugel muss das innere Potential stetig in das Äußere übergehen. Das bedeutet, dass die ersten Ableitungen bei r=R übereinstimmen müssen.
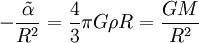 ,
,
wobei wir hier benutzen, dass die Masse das Produkt aus Volumen und Dichte ist, mit
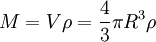 .
.
Hieraus ergibt sich
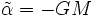 ,
,
so dass sich die bekannte äußere Lösung
ergibt. Um die Konstante der inneren Lösung zu bestimmen, benutzen wir die Tatsache, dass die beiden Lösungen bei r=R identisch sein müssen. D.h. es gilt
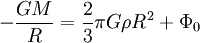 .
.
Und damit
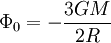 .
.
Damit ergibt sich für die innere Lösung schließlich
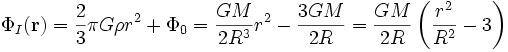 ,
,
wobei der erste Summand wieder über das Volumen umgeschrieben wurde.
Die innere Lösung entspricht einem harmonischen Oszillatorpotential. Das bedeutet, dass wenn man ein Loch durch einen homogenen Himmelskörper (einen Mond oder kleinen Planeten) bohrte und einen Gegenstand hineinfallen ließe, dieser durch den Mittelpunkt hin und her schwingen (fallen) würde. Unter Annahme einer reibungsfreien Bewegung ergibt sich die Ortsfunktion des Körpers zu
Schwerkraft in einer Hohlkugel
Wie die Situation im Innern einer hohlen Kugel aussieht, lässt sich nun auch direkt aus unserer Lösung für ρ = 0 ablesen. Allgemein hatten wir
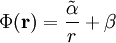 ,
,
da wir uns nun im Innern der Kugel befinden, können wir nicht ins Unendliche hinausgehen, wodurch vorher β verschwunden ist. Allerdings muss das Potential im Mittelpunkt wieder einen endlichen Wert annehmen, so dass dieses mal
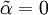 wird. Dann ist das Potential
wird. Dann ist das Potential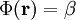 ,
,
also konstant. Die Ableitung des Potentials nach dem Radius ergibt die Beschleunigung – die Ableitung einer Konstanten ist jedoch Null. Also ist man im Innern einer hohlen Kugel schwerelos. Dies ist dadurch zu verstehen, dass gegenüberliegende Teilchen in den Wänden ihre Gravitation gerade gegenseitig aufheben. Handelte es sich nicht um eine perfekte Kugel, so wäre dies nicht der Fall und man würde kleine Beschleunigungen erfahren.
Zentralpotential
Unter einem Zentralpotential versteht man ein Potential, das nur vom Abstand r zum Kraftzentrum abhängt. Es gilt also
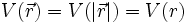 .
.Die Bewegung in einem Zentralpotential führt zu einer Zentralkraft.
Weblinks
- Helmut Föll: Potential – Definition math.-vektoriell. In: Einführung in die Materialwissenschaft II. Abgerufen am 1. Apr. 2009.
Wikimedia Foundation.