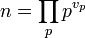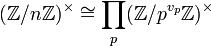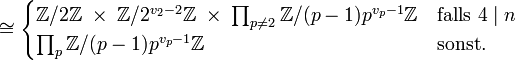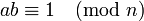Prime Restklasse

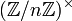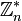Die prime Restklassengruppe ist die Gruppe der primen Restklassen bezüglich eines Moduls n. Sie wird mit $(\mathbb{Z} /n\mathbb{Z} )^\times$ oder $\mathbb{Z}_n^*$ symbolisiert.

Die Gruppe besteht aus den Restklassen 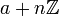$a + n \Z$, deren Elemente zu n teilerfremd sind: 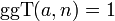$\operatorname{ggT}(a,n) = 1$. Darauf weist die Bezeichnung „prime Restklasse“ hin; für teilerfremd sagt man auch relativ prim. Die Gruppenordnung ist somit φ(n); siehe Eulersche φ-Funktion.

Die Verknüpfung der Gruppe entspricht der Multiplikation von ganzen Zahlen: $(a + n \Z) \cdot (b + n \Z) = (a \cdot b + n \Z)$.

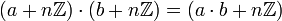Die primen Restklassengruppen sind endliche abelsche Gruppen bezüglich der Multiplikation. Sie spielen in der Kryptografie eine bedeutende Rolle.

Struktur

Bezeichnet v_p die p-Bewertung von n (die Vielfachheit des Primfaktors p in n), ist also

$n=\prod_p p^{v_p}$

die Primfaktorzerlegung von n, dann gilt:

$(\mathbb Z/n\mathbb Z)^\times \cong \prod_p(\mathbb Z/p^{v_p}\mathbb Z)^\times$

${}\cong\begin{cases}\mathbb Z/2\mathbb Z \; \times \; \mathbb Z/2^{v_2-2}\mathbb Z \; \times \; \prod_{p \neq 2}\mathbb Z/(p-1)p^{v_p-1}\mathbb Z&\mathrm{falls}\ 4\mid n\\ \prod_p\mathbb Z/(p-1)p^{v_p-1}\mathbb Z&\mathrm{sonst}.\end{cases}$

Die erste Isomorphieaussage (Zerlegung des Moduls n in seine Primfaktoren) folgt aus dem chinesischen Restsatz. Die zweite Isomorphieaussage (Struktur der primen Restklassengruppe modulo Primzahlpotenz) folgt aus der Existenz gewisser Primitivwurzeln^[1] (siehe auch den zugehörigen Hauptartikel Primitivwurzel).

Beachte: Mit den Gruppen ohne 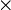$\times$ sind die additiven Gruppen 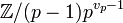$\mathbb Z/(p-1)p^{v_p-1}$ etc. gemeint!

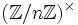$(\mathbb Z/n\mathbb Z)^\times$ ist genau dann zyklisch, wenn n gleich 1,2,4,p^r oder 2p^r ist mit einer ungeraden Primzahl p und einer positiven Ganzzahl r. Genau dann existieren auch Primitivwurzeln modulo n, also Ganzzahlen a, deren Restklasse 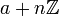$a + n \Z$ ein Erzeuger von 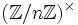$(\mathbb Z/n\mathbb Z)^\times$ ist.

Berechnung der inversen Elemente

Zu jeder primen Restklasse 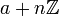$a + n \Z$ existiert eine prime Restklasse 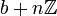$b + n \Z$, sodass gilt:

$ab \equiv 1 \pmod n$

Die prime Restklassengruppe 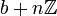$b + n \Z$ ist also das inverse Element zu 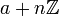$a + n \Z$ bezüglich der Multiplikation in der primen Restklassengruppe 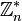$\Z_n^*$. Ein Repräsentant von 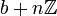$b + n \Z$ lässt sich mit Hilfe des Erweiterten Euklidischen Algorithmus bestimmen. Indem man die obige Kongruenz umschreibt zu

ab + kn = 1

sieht man, dass der Erweiterte Euklidische Algorithmus auf a und n angewandt mit b einen Repräsentanten von 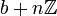$b + n \Z$ berechnet.

Literatur

Die Disquisitiones Arithmeticae wurden von Carl Friedrich Gauß auf Lateinisch veröffentlicht. Die zeitgenössische deutsche Übersetzung umfasst alle seine Schriften zur Zahlentheorie:

• Carl Friedrich Gauß: Untersuchungen über höhere Arithmetik (deutsche Übersetzung), Original: Leipzig 1801.

• Armin Leutbecher: Zahlentheorie - Eine Einführung in die Algebra. 1. Auflage. Springer Verlag, 1996, Berlin Heidelberg New York. ISBN 3-540-58791-8.

Einzelnachweise

1. ↑ A. Leutbecher: Zahlentheorie - Eine Einführung in die Algebra, S. 53-54.

Siehe auch

Restklassenring