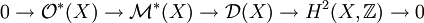- Produktsatz von Weierstraß
-
Der Weierstraßsche Produktsatz für
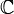 besagt, dass zu einer vorgegebenen Nullstellenverteilung in
besagt, dass zu einer vorgegebenen Nullstellenverteilung in 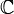 eine holomorphe Funktion mit genau diesen Nullstellen existiert. Die Funktion kann als sogenanntes Weierstraß-Produkt explizit konstruiert werden. Der Satz wurde 1876 von Karl Weierstraß gefunden.
eine holomorphe Funktion mit genau diesen Nullstellen existiert. Die Funktion kann als sogenanntes Weierstraß-Produkt explizit konstruiert werden. Der Satz wurde 1876 von Karl Weierstraß gefunden.Inhaltsverzeichnis
Motivation
Zu endlich vielen Nullstellen
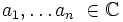 kann man sofort ein Polynom hinschreiben, welches das gestellte Problem löst, beispielsweise
kann man sofort ein Polynom hinschreiben, welches das gestellte Problem löst, beispielsweise 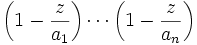 . Im Falle (abzählbar) unendlich vieler Nullstellen wird das Produkt im allgemeinen nicht mehr konvergieren. Ausgehend von der Identität
. Im Falle (abzählbar) unendlich vieler Nullstellen wird das Produkt im allgemeinen nicht mehr konvergieren. Ausgehend von der Identität 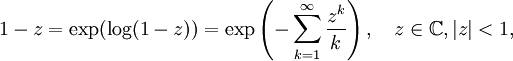 führte Weierstraß deshalb "konvergenzerzeugende" Faktoren ein, indem er die Reihenentwicklung abbrach und Faktoren
führte Weierstraß deshalb "konvergenzerzeugende" Faktoren ein, indem er die Reihenentwicklung abbrach und Faktoren 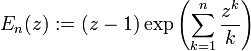 definierte. En hat nur eine Nullstelle bei 1, kann aber im Gegensatz zu 1 − z auf jeder kompakten Teilmenge des Einheitskreises beliebig nahe an 1 liegen, sofern n groß genug gewählt wird. Dadurch kann auch die Konvergenz eines unendlichen Produktes erreicht werden.
definierte. En hat nur eine Nullstelle bei 1, kann aber im Gegensatz zu 1 − z auf jeder kompakten Teilmenge des Einheitskreises beliebig nahe an 1 liegen, sofern n groß genug gewählt wird. Dadurch kann auch die Konvergenz eines unendlichen Produktes erreicht werden.Weierstraß-Produkt
Es sei D ein positiver Divisor im Bereich
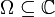 und ak eine so gewählte Folge, dass
und ak eine so gewählte Folge, dass 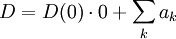 ; Das heißt, die Folge durchläuft mit Ausnahme des Nullpunktes alle Punkte des Trägers von D mit der nötigen Multiplizität. Sie heißt die zum Divisor D gehörende Folge. Ein Produkt
; Das heißt, die Folge durchläuft mit Ausnahme des Nullpunktes alle Punkte des Trägers von D mit der nötigen Multiplizität. Sie heißt die zum Divisor D gehörende Folge. Ein Produkt 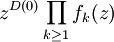 heißt Weierstrass-Produkt zum Divisor D, falls gilt:
heißt Weierstrass-Produkt zum Divisor D, falls gilt:- fk holomorph in Ω
- fk hat genau eine Nullstelle, und zwar in ak und von der Multiplizität 1
- Das Produkt
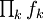 konvergiert normal auf jeder kompakten Teilmenge von Ω.
konvergiert normal auf jeder kompakten Teilmenge von Ω.
Produktsatz in
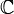
Zu jedem positiven Divisor D in
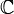 existieren Weierstrass-Produkte der Form
existieren Weierstrass-Produkte der Form 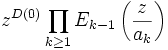 . Dabei sei ak die zum Divisor D gehörende Folge.
. Dabei sei ak die zum Divisor D gehörende Folge.Folgerungen in
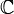
- Zu jedem Divisor gibt es eine meromorphe Funktion mit den dadurch vorgegebenen Null- und Polstellen. Jeder Divisor ist ein Hauptdivisor.
- Zu jeder meromorphen Funktion h gibt es zwei holomorphe Funktionen f,g ohne gemeinsame Nullstellen derart, dass h = f / g. Insbesondere ist der Körper der meromorphen Funktionen der Quotientenkörper des Integritätsbereichs der holomorphen Funktionen.
- Im Ring der holomorphen Funktionen besitzt jede nicht-leere Teilmenge einen größten gemeinsamen Teiler, obwohl der Ring nicht faktoriell ist.
Verallgemeinerung für beliebige Bereiche
Es sei
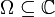 ein Bereich und D ein positiver Divisor auf Ω mit Träger T und es bezeichne
ein Bereich und D ein positiver Divisor auf Ω mit Träger T und es bezeichne 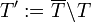 die Menge aller Häufungspunkte von T in
die Menge aller Häufungspunkte von T in 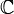 . Dann existieren zum Divisor D Weierstraß-Produkte in
. Dann existieren zum Divisor D Weierstraß-Produkte in 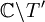 . Sie konvergieren im Allgemeinen also auf einem größeren Bereich als Ω.
. Sie konvergieren im Allgemeinen also auf einem größeren Bereich als Ω.Verallgemeinerung für Steinsche Mannigfaltigkeiten
Eine erste Verallgemeinerung des Produktsatzes für andere komplexe Mannigfaltigkeiten gelang 1895 Pierre Cousin, der den Satz für Zylindergebiete im
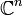 bewies. Aus diesem Grund wird die Frage, ob zu einem vorgegebenem Divisor eine passende meromorphe Funktion konstruiert werden kann, auch als Cousin-Problem bezeichnet.
bewies. Aus diesem Grund wird die Frage, ob zu einem vorgegebenem Divisor eine passende meromorphe Funktion konstruiert werden kann, auch als Cousin-Problem bezeichnet.Jean-Pierre Serre löste 1953 das Cousin-Problem endgültig und zeigte: In einer Steinschen Mannigfaltigkeit X ist ein Divisor genau dann der Divisor einer meromorphen Funktion, wenn seine Chernsche Kohomologieklasse in
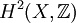 verschwindet. Insbesondere ist in einer Steinschen Mannigfaltigkeit mit
verschwindet. Insbesondere ist in einer Steinschen Mannigfaltigkeit mit 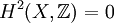 jeder Divisor ein Hauptdivisor. Dies ist die unmittelbare Folgerung daraus, dass in Steinschen Mannigfaltigkeiten folgende Sequenz exakt ist, wobei
jeder Divisor ein Hauptdivisor. Dies ist die unmittelbare Folgerung daraus, dass in Steinschen Mannigfaltigkeiten folgende Sequenz exakt ist, wobei 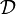 die Garbe der Divisoren bezeichnet:
die Garbe der Divisoren bezeichnet:Literatur
- Reinhold Remmert, Georg Schumacher: Funktionentheorie 2. Springer, Berlin 2007, ISBN 978-3-540-57052-3
- Hans Grauert, Reinhold Remmert: Theory of Stein Spaces. Springer, Berlin 2004, ISBN 3-540-00373-8
Wikimedia Foundation.