- Rechenstäbe
-
Ein Rechenschieber oder Rechenstab ist ein analoges Rechenhilfsmittel zur mechanisch-optischen Durchführung von Grundrechenarten, vorzugsweise der Multiplikation und Division. Je nach Ausführung können auch komplexere Rechenoperationen (unter anderem Wurzel, Quadrat, Logarithmus und trigonometrische Funktionen oder parametrisierte Umrechnungen) ausgeführt werden. Das Prinzip eines Rechenschiebers besteht in der Addition oder Subtraktion von Strecken, die sich als Skalen auf dem festen und dem beweglichen Teil des Rechenschiebers befinden. Bis zur Erfindung des Taschenrechners und der weiten Verbreitung von PCs waren Rechenschieber für viele Berechnungen in Schule, Wissenschaft und Technik unentbehrlich.
Inhaltsverzeichnis
- 1 Geschichte
- 2 Anwendungen
- 3 Aufbau
- 4 Funktionsweise
- 5 Uhren
- 6 Vor- und Nachteile
- 7 Siehe auch
- 8 Literatur
- 9 Weblinks
Geschichte
Entwicklung der Logarithmen
Die Geschichte des Rechenschiebers basiert auf der Entwicklung der Logarithmen. Obwohl es indische Quellen aus dem 2. Jahrhundert v. Chr. gibt, in welchen bereits Logarithmen zur Basis 2 erwähnt wurden, waren es der Schweizer Uhrmacher Jost Bürgi (1558–1632) und der schottische Mathematiker John Napier (1550–1617), die zu Beginn des 17. Jahrhunderts das erste bekannte System zur Logarithmenberechnung unabhängig voneinander entwickelten.
Das griechische Wort „Logarithmus“ bedeutet auf Deutsch Verhältniszahl und stammt von Napier. Erstmals veröffentlicht wurden Logarithmen von diesem unter dem Titel Mirifici logarithmorum canonis descriptio, was mit Beschreibung des wunderbaren Kanons der Logarithmen übersetzt werden kann.
Nachdem sich der Oxforder Professor Henry Briggs (1561–1630) intensiv mit dieser Schrift beschäftigte, nahm er mit deren Autor Kontakt auf und schlug vor, für die Logarithmen die Basis 10 zu verwenden („briggssche“ bzw. „dekadische“ Logarithmen). Diese verbreiteten sich schnell und wurden besonders in der Astronomie geschätzt, was auch Laplace feststellte:
„Durch die Arbeitserleichterung infolge der Verwendung von Logarithmen wird das Leben der Astronomen verdoppelt“.
Heute wird als Basis des so genannten natürlichen Logarithmus die Eulersche Zahl e = 2,718281828459… verwendet, welche im Jahre 1728 von Leonhard Euler (1707–1783) bestimmt und erstmals 1742 veröffentlicht wurde.
Mit den Logarithmen war die mathematische Grundlage für die Weiterentwicklung des mechanischen Rechenschiebers gelegt; denn die Funktionsweise des Rechenschiebers basiert für die Multiplikation und Division auf dem Prinzip der Addition bzw. Subtraktion von Logarithmen.
Entwicklung des Rechenschiebers
Schon 1624, zehn Jahre nach der Erkenntnis der Existenz der Logarithmen durch John Napier von Merchiston, gab der englische Theologe und Mathematiker Edmund Gunter (1581–1626) erstmals seine Grundgedanken über die logarithmischen Zahlen bekannt. Mit der von ihm entwickelten „Gunterskala“, einem Stab mit logarithmisch angeordneter Skala, konnte man anfänglich nur mit Hilfe eines Stechzirkels Additions- und Subtraktionsberechnungen durchführen, indem man die logarithmischen Strecken abgriff. Das Berechnen mit dem Zirkel war jedoch sehr aufwändig und arbeitsintensiv. Daher war die Idee des Engländers William Oughtred (1574–1660) im Jahre 1622, anstelle des Stechzirkels zwei kongruente logarithmische Skalen gerade oder auch kreisförmig zu verwenden, sehr bedeutend. William Oughtred gilt hiermit als der eigentliche Erfinder des Rechenschiebers.
Doch auch Seth Partridge trug 1654 dazu bei, den Rechenschieber weiterzuentwickeln. Von ihm stammt die Idee der ebenfalls logarithmisch skalierten Zunge, welche man gegen den Stabkörper verschieben kann, wodurch Berechnungen wesentlich einfacher ausgeführt werden konnten.
Im Jahr 1722 benutzte Warner erstmals Quadrat- und Kubikskalen. Der von Isaac Newton (1643–1727) erfundene Läufer, welcher auch als Indikator bezeichnet wird, wurde 1775 von John Robertson (1712–1776) umgesetzt. Er blieb jedoch über hundert Jahre lang unbekannt. Diese äußerst praktische Weiterentwicklung ermöglicht durch ihre Querstrich-Markierung die Verbindung von zwei sich nicht berührenden Skalen und erhöht somit die Genauigkeit der Zungeneinstellung bzw. der Ablesung.
Die doppellogarithmischen Exponentialskalen, welche sich meist auf der Rückseite der Zunge befinden, wurden 1815 von dem englischen Arzt und Lexikographen Peter Mark Roget (1779–1869) erfunden. Sie dienen zur Vereinfachung von Exponentialaufgaben jeglicher Art.
Eine große Bedeutung in der Geschichte des Rechenschiebers kommt dem Franzosen Victor Amédée Mannheim (1831–1906) zu, welcher im Jahre 1850 einen einheitlichen Aufbau für den bis zuletzt verwendeten Schulrechenstab durchsetzte. Mit diesem neuen Standardrechenschieber namens „Mannheim“, der aus der Kubikskala K, den Quadratskalen A und B, den Grundskalen C und D sowie der Sinus- und der Tangensskala besteht, wurde auch der seit dieser Ausführung transparente Läufer etabliert. Auch „Dennert (1886), Cox (1897), Beghin (1899), Fürle (1899), Schweth (1901) und Rietz (1902) und Walther […] (1936)“ veränderten und verbesserten den Rechenschieber, zum Beispiel mit materiellen Weiterentwicklungen wie der Verwendung von Kunststoff statt Holz.
Das Ende des Rechenschiebers
Die Erfindung des Taschenrechners im Jahre 1969 löste einen regelrechten Boom in der Entwicklung dieses neuen, sehr gefragten Recheninstrumentes aus. Bereits 1972 entstand der erste wissenschaftliche Taschenrechner, welcher mit wesentlich mehr Funktionen ausgestattet war. Zudem konnte der Taschenrechner durch die erhöhte Produktion aufgrund der immensen Nachfrage immer günstiger erworben werden. Um 1975 begannen auch die Schulen, den elektronischen Taschenrechner anstelle des mechanischen Rechenschiebers einzusetzen, was letztendlich das Ende für den damals als unentbehrlich geltenden Rechenstab und somit auch für seine Hersteller bedeutete. In der DDR begann erst Mitte der 1980er Jahre der Einsatz des Taschenrechners in der Polytechnischen Oberschule. Daher ist der Rechenschieber heute nicht mehr von großer Bedeutung – nur noch wenige junge Menschen kennen ihn, kaum einer weiß mehr mit ihm umzugehen. Schließlich ist der Taschenrechner günstiger, genauer und bequemer in der Handhabung.
Dennoch ziehen manche den Rechenschieber dem Taschenrechner vor, da sie schon seit der Schulzeit damit rechnen und schnell und versiert Rechnungen damit ausführen können. Es gibt aber auch Privatpersonen, welche Rechenschieber aus nostalgischen Gründen behalten, und Sammler, deren Leidenschaft es ist, seltene Modelle zu tauschen oder sie zu erwerben – meist durch Kontakte oder Internetauktionshäuser. In Deutschland, jedoch auch auf internationaler Ebene wie zum Beispiel durch die seit 1991 existierende „Oughtred Society“, finden regelmäßig Treffen von Rechenschiebersammlern statt, bei denen diese ihr Sortiment und ihr Wissen über den Rechenschieber erweitern können. Gelegentlich werden dort auch sehr seltene Exemplare ausgestellt, die unter Sammlern Preise von über 100.000 Dollar erzielen. Die wohl begehrtesten Rechenschieber, die vier Originalrechenstäbe von William Oughtred, von denen jeder einzelne über 250.000 US-Dollar wert ist, befinden sich allesamt in Museen.
Hersteller von Rechenstäben
In Deutschland wurden Rechenstäbe z. B. von Aristo (Dennert & Pape) in Hamburg, A. W. Faber Castell in Stein bei Nürnberg, Nestler in Lahr und dem VEB Mantissa Mono-Rietz in Dresden hergestellt.
Anwendungen
In den ersten zweihundert Jahren nach seiner Erfindung wurde der Rechenschieber sehr wenig genutzt. Erst Ende des 17. Jahrhunderts wurde seine Bedeutung von James Watt neu erkannt.
Aufgrund des technischen Fortschritts in der Zeit der Industriellen Revolution wurde der Rechenschieber ein vielbenutztes Instrument für technische und wissenschaftliche Berechnungen. Seitdem galt er als das Symbol der Ingenieure, Mathematiker und Physiker.
Neben den Schulrechenstäben, die im Unterricht und bei einfachen Berechnungen im Alltag ihre Nutzung fanden, wurden auch viele Sonderrechenstäbe hergestellt, die oft in sehr speziellen Bereichen wie zum Beispiel in der Luftfahrt, der Elektro- und Anlagentechnik, der Chemie, beim Militär oder im Handel eingesetzt wurden.
Aufbau
Ein Rechenschieber besteht aus einem Körper, auf dem meist mehrere parallel angeordnete Skalen angebracht sind, einer beweglichen Zunge mit gleichartigen eigenen Skalen sowie einem auf dem Körper verschiebbaren Läufer mit einer Querstrich-Markierung. Durch Verschieben der Skalen gegeneinander wird die Rechenoperation durchgeführt und an der entsprechenden Zahlenwertstelle abgelesen. Die Läufermarkierung erlaubt vor allem das Ablesen an den auseinander liegenden parallelen Skalen, die sich an den Kanten von Körper und Zunge nicht direkt berühren.
Die Standardskalenlänge – gemessen von der Marke „1“ bis zur Marke „10“ – der Rechenschiebermodelle ist 25 cm; kleine Ausführungen (z. B.Taschenmodelle) haben eine Skalenlänge von 12,5 cm, Büro- oder Tischmodelle von 50 cm.
Varianten des Rechenschiebers sind
- die Rechenscheibe, d. h. ein Rechenschieber, der nicht als gerader Stab, sondern kreisförmig ausgelegt ist, auch auf der Rückseite einiger Parkscheiben zu finden, und
- die Rechenwalze, d. h. ein Rechenschieber, dessen Skalen auf viele (typischerweise einige Dutzend) Teile aufgeteilt zylindrisch angeordnet sind, wodurch eine größere effektive Skalenlänge (typischerweise einige Meter) und damit eine höhere Genauigkeit erreicht wird.
Da man mit dem Rechenschieber nicht addieren und subtrahieren kann, gibt es auch Ausführungen, die auf der Rückseite einen Zahlenschieber oder Griffeladdierer haben.
 Rechenschieber zur Bestimmung der Arbeitsparameter einer Werkzeugmaschine
Rechenschieber zur Bestimmung der Arbeitsparameter einer WerkzeugmaschineAuf Rechenschiebern können spezielle Tabellen aufgedruckt werden, die in der Anordnung ganze Formeln beinhalten. So kann man ihn durch Verschieben der Parameter in der Technik zur Auswahl von Lagern oder Keilriemen verwenden und ersetzt damit ganze Tabellenbücher.
Funktionsweise
Es gibt eine ganze Reihe unterschiedlicher Rechenschieber. Die grundlegenden Ideen sind jedoch alle in etwa mit dem folgenden Beispiel vergleichbar:
Auf einen Stab bzw. Schieber existieren mehrere (meist logarithmische) Skalen, die jede eine spezielle Funktion haben.
In unserem Beispiel (siehe Bild 1) sind sieben Skalen vorhanden, die hier mit den Buchstaben 'a' bis 'g' bezeichnet werden. Die drei mittleren Skalen 'c', 'd' und 'e' können verschoben werden (siehe Bild 2). Zudem existiert auch noch eine Fadenlinie zum Abgleichen der verschiedenen Skalen. Jede Skala steht in einer genau vordefinierten Funktion zu den anderen Skalen (siehe Tabelle 1):
Bezeichnung Skala Bereich Funktion bzw. Funktionen Bemerkung a linear [0].0 bis [1].0 log10b / b logarithmisch 1..10 ![b, 10^a, \sqrt{f}, \sqrt[3]{g}](/pictures/dewiki/57/978bc5eb1857224cb995b08dbb4a3791.png)
Hauptskala c logarithmisch 1..10 Hauptskala auf der Zunge d logarithmisch 10..1 b − 1 „Divisor“ der Hauptskala e logarithmisch 1..100 Zweite Hauptskala auf der Zunge f logarithmisch 1..100 b2 Zweite Hauptskala g logarithmisch 1..1000 b3 Skala zum Bestimmen des Volumens Kommastellen
Mit dem Rechenschieber erhält man zunächst nur die ungefähr dreistellige Ziffernfolge des Ergebnisses. Daher muss man stets eine grobe Überschlagsrechnung durchführen, um das Komma an die richtige Stelle setzen zu können. Dies ist für die korrekte Anwendung des Rechenschiebers unerlässlich und bei jeder Aufgabe erforderlich. Die Kommastellen in den folgenden Rechenbeispielen stehen demnach nicht zwingend an der richtigen Stelle, sondern so, wie sie auf dem Rechenschieber abgebildet sind.
Multiplikation
Man kann die Faktoren des Logarithmus auf zwei Logarithmen aufteilen und schließlich summieren.
Da die Skalen C und D auf dem Rechenschieber logarithmisch sind, erhält man durch die Addition zweier Strecken mit Hilfe dieser Skalen eine Summe aus zwei Logarithmen. Dies erreicht man, indem man den Zungenanfang der C-Skala über den ersten Faktor der D-Skala schiebt. Der Läufer wird jetzt über den zweiten Faktor auf der C-Skala geschoben, so dass das Ergebnis bei D abgelesen werden kann. Da die Summe der Einzel-Logarithmen der Logarithmus des Produktes ist, entspricht der abzulesende Summenwert dem Produkt.
Übersteigt das Produkt den Wert 10, lässt sich dieses nicht auf die beschriebene Weise ablesen. Man stellt sich nun vor, dass man eine virtuelle zweite D-Skala an das Zungenende der ersten anhängt. Dies entspricht dann einer Verschiebung der 10 der C-Skala über den ersten Faktor der D-Skala. Das Produkt lässt sich dann mit Hilfe des Läufers unter dem zweiten Faktor der C-Skala auf D ablesen. Dieses Vorgehen wird „Durchschieben“ bzw. „Rückschlag“ der Zunge genannt.
Nach derselben Methode kann man auch bei der Multiplikation zweier Faktoren auf den Skalen A und B vorgehen. Man wendet dies jedoch meist nur dann an, wenn einer der Faktoren eine Quadratzahl ist oder wenn man eine Wurzel aus zwei Faktoren ziehen will. Für die einfache Multiplikation ist diese Vorgehensweise eher unüblich, da die Skalen A und B nur halb so groß wie die Skalen C und D sind und man daher eine geringere Genauigkeit erhält.
Division
Die Division ist die Umkehrung der Multiplikation. Man kann somit den Quotienten über eine Differenz von Logarithmen ermitteln.
Durch die logarithmische Teilung der Skalen C und D verschiebt man die Zunge so, dass der Dividend auf der D-Skala unter dem Divisor auf der C-Skala steht. Der Quotient entspricht der Differenz der logarithmischen Strecken. Man kann ihn sofort an der D-Skala unter dem Zungenanfang der C-Skala ablesen, ohne den Läufer einmal verschoben zu haben. Das zuvor erklärte Durchschieben der Zunge gilt ebenfalls bei der Division. Das Ergebnis steht in diesem Fall am Zungenende.
Proportionen
Das Verhältnis zwischen den Werten auf den Skalen A und B bzw. C und D ist bei fester Zungeneinstellung immer proportional.
Somit eignet sich der Rechenschieber sehr gut für Proportionalrechnung bzw. für Dreisatzaufgaben. Hierbei ist es hilfreich, vor der Multiplikation die Division durchzuführen, da sich die Aufgabe dann meist durch eine einzige Zungeneinstellung berechnen lässt.
Ein wesentlicher Vorteil des Rechenschiebers liegt bei Dreisatzrechnungen darin, dass aufgrund der proportionalen Lage der Skalen nicht nur das Ergebnis für den zweiten Faktor, sondern bei gleicher Zungeneinstellung für beliebig viele weitere Faktoren abgelesen werden kann.
Potenzen
Quadratzahlen
Um zu quadrieren, benötigt man die Quadrat-Skalen A und B, auf welchen jeweils zwei logarithmische Leitern der Länge 12,5 cm abgebildet sind. Die Einheit dieser Leitern ist also nur halb so groß wie die Einheit der Grundskalen C und D.
Um zu quadrieren, stellt man die Zahl mit dem Läufer auf D bzw. C ein und liest anschließend das Quadrat bei A bzw. bei B ab.
Kubikzahlen
Auf der Kubik-Skala K befinden sich drei logarithmische Leitern. Die Länge einer Leiter beträgt ein Drittel der Länge der Grundskalen C und D.
Um mit 3 zu potenzieren, markiert man mit dem Läufer die Zahl auf der D-Skala. Die gesuchte Kubikzahl steht dann bei K. Da sich die Kubikskala auf dem Stabkörper befindet, ist eine Einstellung auf der C-Skala nicht sinnvoll.
Wurzeln
Quadratwurzel
Da sich aber auf den Quadrat-Skalen A und B jeweils zwei logarithmische Leitern befinden, muss man beim Ziehen von Quadratwurzeln Folgendes beachten:
Will man die Wurzel aus einer Zahl ziehen, die vor dem Komma eine ungerade Anzahl an Ziffern hat, so ist diese Zahl zwischen 1 und 10 auf der ersten Leiter von A bzw. B einzustellen. Ist die Anzahl der Stellen des Radikanden dahingegen gerade, so verwendet man die zweite Leiter und stellt die Zahl zwischen 10 und 100 ein. Das Ergebnis lässt sich dann auf der Grundskala D ablesen.
Ist der Radikand kleiner als 1, so wird er so oft mit 100 multipliziert, bis er den Wert 1 überschreitet. Liegt dieses Produkt zwischen 1 und 10, so gilt die Stellenzahl als ungerade, der Radikand wird also in der linken Hälfte auf A bzw. B eingestellt. Ist es größer als 10, so gilt die Stellenzahl als gerade, der Radikand wird also in der rechten Hälfte festgehalten. Wiederum steht das Ergebnis auf D.
Kubikwurzel
Auf der K-Skala sind drei logarithmische Leitern abgebildet, eine von 1 bis 10, eine von 10 bis 100 und eine von 100 bis 1000. Möchte man die Kubikwurzel einer Zahl ermitteln, deren Wert zwischen 1 und 1000 liegt, so stellt man diese Zahl mit dem Läufer auf der K-Skala ein und liest das Ergebnis bei D ab.
Ist die Kubikwurzel aus einer Zahl zu ziehen, deren Wert nicht zwischen 1 und 1000 liegt, so wird der Radikand, vom Komma ausgehend, in Gruppen zu je drei Ziffern nach links bzw. bei Zahlen kleiner als 1 nach rechts aufgeteilt. Liegt der Wert der ersten Gruppe, die mindestens eine geltende Ziffer enthält, zwischen 1 und 10, so stellt man den Radikanden im linken Drittel der Kubikskala K ein; liegt die Zahl zwischen 10 und 100, verwendet man das mittlere Drittel; liegt sie zwischen 100 und 1000, so wird das rechte Drittel verwendet.
Kehrwerte
Die rot bezifferte Reziprok-Skala (Kehrwert-Skala) CI (Abk. für „C invers“) befindet sich auf der Zunge des Rechenschiebers und verläuft – im Gegensatz zu allen anderen Skalen – von rechts nach links. Sie stellt spiegelbildlich die C-Skala dar und dient somit zur Berechnung der Kehrwerte.
Addiert man nämlich mit dem Rechenschieber den Logarithmus einer Zahl zum Logarithmus von deren Kehrwert, so lässt sich das Ergebnis am Endstrich ablesen, also beim Logarithmus der Zahl 10. Da es beim Rechnen mit dem Rechenschieber lediglich auf die Ziffernfolge des Ergebnisses ankommt, kann die Zahl 10 durch 1 ersetzt werden. Ein Kehrwert lässt sich somit unmittelbar oberhalb des eigentlichen Wertes der Skala C auf der CI-Skala ablesen.
Mit Hilfe der Reziprok-Skala können Multiplikationen und Divisionen oft vereinfacht werden. Möchte man beispielsweise drei Faktoren miteinander multiplizieren, erweist es sich als vorteilhaft, zuerst die Faktoren mit Hilfe der D-Skala und der CI-Skala zu multiplizieren. Dazu verschiebt man die Zunge so, dass der erste Faktor der D-Skala unter dem zweiten Faktor der Kehrwert-Skala CI steht. Der Zungenanfang bzw. das Zungenende stehen dann auf diesem Produkt, sodass man nur noch den Läufer auf den dritten Faktor der C-Skala schieben muss und das Ergebnis auf der D-Skala ablesen kann. Somit erhält man das Ergebnis oft nach einer einzigen Zungeneinstellung.
Logarithmen-Bestimmung
Um Logarithmen bestimmen zu können, benötigt man die gleichmäßig geteilte Logarithmen-Skala L, welche ebenfalls auf der Zunge des Rechenstabs aufgetragen ist. Durch die Logarithmen-Skala erhält man keine Ziffernfolge, sondern lediglich die Mantisse des Ergebnisses.
Möchte man den Zehnerlogarithmus einer Zahl herausfinden, so fixiert man den Logarithmanden mit dem Läufer auf C und liest die Mantisse auf der Skala L ab. Zu diesen Nachkommastellen addiert man nun die Anzahl der Stellen des Logarithmanden, die vor dem Komma stehen, und zieht davon wiederum 1 ab.
Die Logarithmen-Bestimmung wird vor allem zur Bestimmung von Potenzen und Wurzeln beliebiger Exponenten verwendet. Da jedoch durch jeden kleinen Fehler bei der Ermittlung des Logarithmus die Genauigkeit deutlich beeinträchtigt wird, dient diese Methode lediglich für Überschlagsrechnungen.
Trigonometrische Werte
Sinus
Die Sinus-Skala S befindet sich auf dem Stabkörper unterhalb der D-Skala und dient zur Ermittlung der Sinuswerte aufgrund der logarithmischen Anordnung der Zahlen.
Winkel zwischen 5,74° und 90° lassen sich berechnen, indem man mit dem Läufer die Gradzahl auf der S-Skala einstellt und den Wert bei D abliest.
Für Winkel unter 5,74° entspricht die Sinusfunktion ungefähr der Arkusfunktion; die Abweichung beträgt hier weniger als 1,5 ‰. Für solche kleinen Winkel verwendet man deshalb die logarithmische Skala ST der Arkusfunktion, bei der die Teilungen der Funktion entsprechen. Analog stellt man hier die Gradzahl auf der ST-Skala ein, sodass das Ergebnis auf der D-Skala steht.
Ist ein Winkel gegeben, der größer als 90° ist, so muss dieser Winkel erst auf einen spitzen Winkel zurückgeführt werden, der den gleichen Funktionswert liefert.
Eine weitere Möglichkeit zur Berechnung eines Sinuswertes ist, ihn geeignet über einen Kosinuswert zu ermitteln.
Kosinus
Die rot bezifferte Kosinus-Skala, die sich ebenfalls auf der Sinus-Skala befindet, ermöglicht die Berechnung des Kosinuswertes für spitze Winkel und verläuft von rechts nach links.
Ist ein Winkel gegeben, der größer als 90° ist, so muss dieser Winkel erst auf einen spitzen Winkel zurückgeführt werden, der den gleichen Funktionswert liefert.
Tangens
Zur Berechnung der Tangenswerte benötigt man die Skalen T1 und T2, wobei man T1 für Werte zwischen 5,71° und 45° und T2 für Werte zwischen 45° und 84,29° verwendet.
Tangenswerte für Winkel kleiner als 5,71° lassen sich – wie beim Sinus – durch Fixierung der Gradzahl mit dem Läufer auf ST auf der D-Skala ablesen.
Werte für Winkel zwischen 84,29° und 90° erhält man durch die Umrechnung tan x = 1 / tan (90°−x).
Ist ein Winkel gegeben, der größer als 90° ist, so muss dieser Winkel erst auf einen spitzen Winkel zurückgeführt werden, der den gleichen Funktionswert liefert.
Addition und Subtraktion
Additionen und Subtraktionen sind nur mit Spezialrechenschiebern möglich, die neben den (oder anstelle der) logarithmisch geteilten Skalen (auch) lineare Skalen besitzen. Sie werden mit diesen Skalen genauso ausgeführt wie Mulitiplikationen und Divisionen mit den logarithmischen Skalen, also durch Aneinanderfügung der entsprechenden Strecken.
Rechenbeispiel 1
Aufgabe: Bestimme die Quadratwurzel von 30 mit dem Rechenschieber.
Dazu wird die Fadenlinie auf '30' der Skala 'f' gesetzt, und das Resultat wird auf der Skala 'b' abgelesen. So findet man 5,48, was der auf zwei Stellen gerundeten Darstellung des exakten Resultates von 5,4772256... entspricht.
Rechenbeispiel 2
Aufgabe: Bestimme
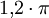 mit Hilfe des Rechenschiebers.
mit Hilfe des Rechenschiebers.Dazu wird die '1' der Skala 'c' neben die '1,2' auf der Skala b geschoben (siehe Bild 2). Anschließend wird die blaue Fadenlinie auf den Wert π auf der Skala 'c' verschoben, und das Resultat wird auf der Skala 'b' abgelesen. So findet man den Wert von 3,77 (genauer 3,7699112...).
Zusätzlich kann man noch als Bonus auf den anderen Skalen direkt folgende Werte ablesen, falls benötigt:
- Skala 'a':
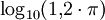 : 0,577 (genauer 0,57633112…)
: 0,577 (genauer 0,57633112…) - Skala 'f':
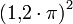 : 14,2 (genauer 14,212230…)
: 14,2 (genauer 14,212230…) - Skala 'g':
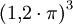 : 53,5 (genauer 53,578846…)
: 53,5 (genauer 53,578846…)
Rechenbeispiel 3
Aufgabe: Berechne
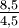 mit dem Rechenschieber.
mit dem Rechenschieber.Dazu wird die „1“ auf der Skala 'd' neben der „8,5“ auf der Skala 'b' platziert (siehe Bild 3). Danach wird die blaue Fadenlinie auf den Wert „4,5“ auf der Skala 'd' gesetzt. Anschließend kann das Resultat auf der Skala 'b' abgelesen werden. So findet man 1,89 (exakt 1,8888888…).
Zusätzlich kann man noch als Bonus auf den anderen Skalen folgende Werte ablesen, falls benötigt:
- Skala 'a':
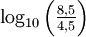 : 0,276 (exakt 0,27620641…)
: 0,276 (exakt 0,27620641…) - Skala 'f':
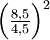 : 3,56 (genauer 3,5679012…)
: 3,56 (genauer 3,5679012…) - Skala 'g':
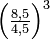 : 6,75 (genauer 6,739369…)
: 6,75 (genauer 6,739369…)
Uhren
Es gibt auch heute noch Armbanduhren, die mit einem Rechenschieber ausgestattet sind, etwa von Breitling, Sinn oder Citizen.
Vor- und Nachteile
Da es bis zu den frühen 1970er Jahren keine Möglichkeit gab, Berechnungen mit dem Taschenrechner oder mit dem Computer durchzuführen, galt der Rechenschieber als das wichtigste Recheninstrument seiner Zeit. Mit der Einführung des Taschenrechners änderte sich dies aber schlagartig; denn der Rechenstab, einst von IBM beworben als ein Gerät, welches 150 Ingenieure ersetzen würde, konnte mit der Funktionsvielfalt des Taschenrechners einfach nicht mithalten.
Doch auch in der Größe war das neue Gerät dem Rechenstab überlegen. Vor 1969 war der Rechenschieber ein kleines und praktisches Gerät, welches man überall mitnehmen konnte. Doch schon der erste Taschenrechner der Welt war kleiner und handlicher als der Standardrechenstab, spätere Generationen des Taschenrechners erreichen sogar Scheckkartengröße und sind damit auch kleiner als die kleinsten Rechenstäbe.
Ein weiterer Grund für die Beliebtheit des Rechenschiebers war die Möglichkeit, schnell damit Ergebnisse zu ermitteln. Auch in dieser Hinsicht war ihm der Taschenrechner seit seinem Erscheinen überlegen, obwohl er auch heute ein sehr bequemes Hilfsmittel zur Berechnung von Dreisatzaufgaben ist, da man mit derselben Stabeinstellung eine ganze Reihe von Ergebnissen ablesen kann.
War früher noch die Genauigkeit in der Technik auf drei Stellen für die meisten Anwendungen ausreichend, so genügt dies in Zeiten von Mikrochips und immer geringeren Fertigungstoleranzen bei weitem nicht mehr.
Eine dem Benutzer zugute kommende Eigenschaft des Stabrechnens ist, dass er durch den Umgang mit dem Rechenschieber aktiv sein mathematisches Verständnis trainiert. Dafür ist nämlich eine gewisse Kenntnis der Logarithmusfunktion vonnöten. Zudem bedarf es auch immer einer Überschlagsrechnung, um sich der Größenordnung des Ergebnisses bewusst zu werden. Somit fördert die Beschäftigung mit dem Rechenschieber auch das logische Denkvermögen. Zugleich ist dieser Anspruch an seinen Benutzer jedoch auch ein Nachteil, da nicht jeder über ein mathematisches Verständnis verfügt oder den Aufwand, den das Erlernen der Funktionsweise mit sich bringt, für angemessen empfindet. So bevorzugen die meisten Menschen eher eine einfache und leicht zu erlernende Bedienung, die ihnen der Taschenrechner bietet.
Ein weiterer Vorteil war die Notwendigkeit, bei Berechnungen die 10er-Potenzen im Kopf mitführen zu müssen, was mit einiger Übung recht gut gelang. Beim Benutzen von Taschenrechnern rutschen Ergebnisse in falsche Regionen, wenn Nullen oder Kommas an der falschen Stelle eingetippt werden. Konsequenz: kritische Rechnungen werden immer zwei mal durchgetippt.
Ein unbestreitbarer Vorteil des Rechenschiebers ist, dass er unabhängig von einer Stromquelle benutzt werden kann.
Siehe auch
Literatur
- Cliff Stoll: Als Rechner noch geschoben wurden, Spektrum der Wissenschaft, April 2007
- Wilhelm Rieck: Stabrechnen in Theorie und Praxis. Verlag Handwerk und Technik, 1971
- Giovanni Pastore: Antikythera e i regoli calcolatori, Eigenverlag des Autors, Rome 2006 Giovanni Pastore, italienisch
Weblinks
Wikimedia Foundation.







