- Satz von Nash
-
Die Verhandlungslösung ist ein spieltheoretisches Konzept zur Lösung von kooperativen Spielen. Dabei heißt ein Spiel kooperativ, wenn die Akteure durch ein abgestimmtes Vorgehen, d. h. durch eine gemeinsame Wahl einer Strategie, einen Zusatzgewinn gegenüber der Situation, in der jeder nur für sich spielt, erzielen können. In diesem Fall ist über die Aufteilung des Zusatzgewinns zu verhandeln, daher der Begriff Verhandlungslösung (engl. bargaining solution). Dieser Artikel beschränkt sich auf so genannte Zweipersonenspiele, also auf Spiele, an denen nur zwei Spieler beteiligt sind.
Die nicht-kooperative Situation
Die meisten Gesellschaftsspiele erfordern häufige strategische Entscheidungen der beteiligten Spieler, um einen für sie günstigen Spielausgang herbeizuführen. Legt man diese Entscheidungen für alle denkbaren Spielsituationen bereits vor Spielbeginn fest, so hat man es nur noch mit einer Strategie pro Spieler zu tun. Die Ausführung des Spiels besteht dann nur noch in der Befolgung der bereits getroffenen Entscheidungen. Das ist die Sichtweise des Mathematikers:
Ein nicht-kooperatives Zweipersonen-Spiel Γ besteht aus zwei Mengen S1 und S2 und zwei Abbildungen
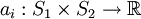 , man schreibt kurz Γ = (S1,S2,(a1,a2)). Das Spiel besteht darin, dass jeder Spieler unabhängig vom anderen ein Element si aus seiner Strategiemenge Si wählt. Der i-te Spieler erzielt daraufhin die Auszahlung ai(s1,s2).
, man schreibt kurz Γ = (S1,S2,(a1,a2)). Das Spiel besteht darin, dass jeder Spieler unabhängig vom anderen ein Element si aus seiner Strategiemenge Si wählt. Der i-te Spieler erzielt daraufhin die Auszahlung ai(s1,s2).Sind die Strategiemengen endlich, so kann man sie nummerieren und etwa
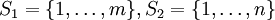 setzen. Die Auszahlungsfunktionen sind dann durch zwei Matrizen
setzen. Die Auszahlungsfunktionen sind dann durch zwei Matrizen 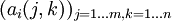 gegeben und man spricht von einem Bimatrixspiel.
gegeben und man spricht von einem Bimatrixspiel.Jeder Spieler kann sich durch Wahl der besten Stategie bei Unterstellung der für ihn ungünstigsten Strategiewahl des Gegenspielers einen gewissen Auszahlungsbetrag garantieren
- Spieler 1:
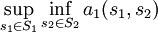
- Spieler 2:
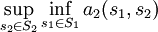 .
.
Das sind die so genannten Garantiewerte der Spieler. Werden Supremum und Infimum nicht angenommen, so hat man immerhin noch approximative Garantien.
Unter einem Nash-Gleichgewicht versteht man ein Paar (s1,s2) von Strategien aus
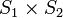 , so dass sich ein Spieler durch einseitiges Abweichen von seiner Strategie höchstens verschlechtern kann. In der Theorie der nicht-kooperativen Spiele, in der ein gemeinsames, abgesprochenes Abweichen nicht vorgesehen ist, kann ein Gleichgewicht als Lösung des Spiels verstanden werden.
, so dass sich ein Spieler durch einseitiges Abweichen von seiner Strategie höchstens verschlechtern kann. In der Theorie der nicht-kooperativen Spiele, in der ein gemeinsames, abgesprochenes Abweichen nicht vorgesehen ist, kann ein Gleichgewicht als Lösung des Spiels verstanden werden.Das Gefangenendilemma
Die wohl bekannteste spieltheoretische Situation, die den Verhandlungbegriff geradezu herausfordert, ist das Gefangenendilemma. Zwei Gefangene werden auf Grund zweifelhafter Beweislage eines gemeinschaftlichen Verbrechens beschuldigt. Jeder hat zwei Strategien zur Auswahl: 1 = Leugnen, 2 = Gestehen. Leugnen beide, so kann nur eine einjährige Haftstrafe verhängt werden, etwa wegen unerlaubten Waffenbesitzes und Ruhestörung. Gestehen beide, so werden je 8 Jahre fällig. Treffen unterschiedliche Strategien aufeinander, so geht der Geständige als Kronzeuge straffrei aus, der Leugner hingegen sieht sich einer 10-jährigen Haft gegenüber. Nimmt man als Auszahlung in diesem Bimatrixspiel das Negative der abzusitzenden Haftjahre, so gilt für die Auszahlungsmatrizen
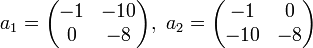
Der einzige Gleichgewichtspunkt ist offenbar (2,2), d. h. beide Gefangene gestehen. (1,1) ist kein Gleichgewicht, da sich jeder Spieler durch einen Strategiewechsel auf Kosten des anderen Straffreiheit sichern kann. Da das jeder Beteiligte weiß, erscheint die Strategiekombination (1,1) sogar sehr instabil.
Dennoch ist (1,1) sicher die optimale Lösung aus der Sicht der Delinquenten. Aber dazu müssten sie eine Absprache treffen können, d. h. über die einzusetzenden Strategien verhandeln. Das wird durch den Begriff der Kooperation modelliert.
Kooperation
Um Verhandlungen mathematisch modellieren zu können, erweitern wir die Definition des nicht-kooperativen Spiels Γ = (S1,S2,(a1,a2)) zu Γ = (S1,S2,K,(a1,a2)) mit
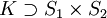 und
und 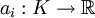 . Wir nennen K die Menge der kooperativen Strategien. Bei Wahl einer kooperativen Strategie k erhält der i-te Spieler die Auszahlung ai(k). Da
. Wir nennen K die Menge der kooperativen Strategien. Bei Wahl einer kooperativen Strategie k erhält der i-te Spieler die Auszahlung ai(k). Da 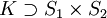 , kann jeder Spieler auch seine eigene Strategie spielen, aber es handelt sich dabei möglicherweise um eine Absprache mit dem Mitspieler, der jetzt nicht mehr als Gegenspieler betrachtet wird.
, kann jeder Spieler auch seine eigene Strategie spielen, aber es handelt sich dabei möglicherweise um eine Absprache mit dem Mitspieler, der jetzt nicht mehr als Gegenspieler betrachtet wird.Das Gefangenendilemma können wir mit
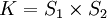 modellieren, es kommt dann nur auf die Absprachemöglichkeit an. Betrachtet man etwa zwei Wirtschaftakteure, die in der nicht-kooperativen Situation eigene Produktionsstrategien für denselben Markt haben, so sind durchaus kooperative Strategien denkbar, die über eine Absprache der Produktionsstrategien hinausgehen, z. B. die Gründung eines Kartells oder die Koordination der Produktion durch Hintereinanderschaltung verschiedener Verarbeitungsstufen. Was als kooperative Strategie erlaubt ist, ist Inhalt der Spielregeln, das Kartellgesetz ist so eine Spielregel.
modellieren, es kommt dann nur auf die Absprachemöglichkeit an. Betrachtet man etwa zwei Wirtschaftakteure, die in der nicht-kooperativen Situation eigene Produktionsstrategien für denselben Markt haben, so sind durchaus kooperative Strategien denkbar, die über eine Absprache der Produktionsstrategien hinausgehen, z. B. die Gründung eines Kartells oder die Koordination der Produktion durch Hintereinanderschaltung verschiedener Verarbeitungsstufen. Was als kooperative Strategie erlaubt ist, ist Inhalt der Spielregeln, das Kartellgesetz ist so eine Spielregel.Verhandlungssituationen
Wir konzentrieren uns nun auf das Bild der gemeinsamen Auszahlungsfunktion (a1,a2) in
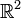 ,
, 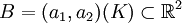 , d. h. wir abstrahieren von den Strategien, die zu diesen Auszahlungen führen. B enthält einen Punkt d = (d1,d2), der aus Auszahlungen besteht, die sich jeder Spieler auch allein sichern kann, z. B. die oben definierten Garantiewerte. Die Spieler werden sicher nur über Auszahlungen x = (x1,x2) verhandeln, bei denen
, d. h. wir abstrahieren von den Strategien, die zu diesen Auszahlungen führen. B enthält einen Punkt d = (d1,d2), der aus Auszahlungen besteht, die sich jeder Spieler auch allein sichern kann, z. B. die oben definierten Garantiewerte. Die Spieler werden sicher nur über Auszahlungen x = (x1,x2) verhandeln, bei denen 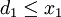 und
und 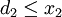 ist, denn sonst wäre ein Spieler mit seinem Garantiewert besser gestellt. Ferner sollte eine mögliche Auszahlung x = (x1,x2) mit d1 < x1 und d2 < x2 existieren, damit es für beide Spieler überhaupt etwas zu verhandeln gibt.
ist, denn sonst wäre ein Spieler mit seinem Garantiewert besser gestellt. Ferner sollte eine mögliche Auszahlung x = (x1,x2) mit d1 < x1 und d2 < x2 existieren, damit es für beide Spieler überhaupt etwas zu verhandeln gibt.Zusätzlich gestatten wir den Spielern eine gemeinsame Wahrscheinlichkeitsverteilung μ auf K zu wählen. Der Auszahlungspunkt errechnet sich dann als Erwartungswert
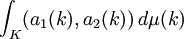 . Die Menge B der möglichen Auszahlungspunkte dürfen wir daher als konvex annehmen, denn durch eine gemeinsame Wahl von μ können die Spieler jede Konvexkombination von Auszahlungspunkten realisieren. Ferner können wir annehmen, dass B beschränkt ist, indem wir unbegrenzte Auszahlungsfunktionen als unrealistisch ausschließen. Nehmen wir B auch noch als abgeschlossen an, ist B sogar kompakt. Das motiviert folgende auf Ehud Kalai und Meir Smorodinsky zurückgehende Begriffsbildung:
. Die Menge B der möglichen Auszahlungspunkte dürfen wir daher als konvex annehmen, denn durch eine gemeinsame Wahl von μ können die Spieler jede Konvexkombination von Auszahlungspunkten realisieren. Ferner können wir annehmen, dass B beschränkt ist, indem wir unbegrenzte Auszahlungsfunktionen als unrealistisch ausschließen. Nehmen wir B auch noch als abgeschlossen an, ist B sogar kompakt. Das motiviert folgende auf Ehud Kalai und Meir Smorodinsky zurückgehende Begriffsbildung:Eine Verhandlungssituation ist ein Paar (B,d) mit folgenden Eigenschaften:
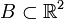 konvex und kompakt,
konvex und kompakt,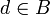 ,
,- für alle
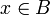 gilt komponentenweise
gilt komponentenweise 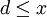 ,
, - es gibt ein
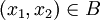 mit d1 < x1 und d2 < x2.
mit d1 < x1 und d2 < x2.
Das Verhandlungsproblem
Ist (B,d) eine Verhandlungssituation, so nennt man die Wahl eines Auszahlungspunktes
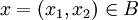 ein Verhandlungsergebnis. Der i-te Spieler erhält die Auszahlung xi. Das Verhandlungsproblem besteht darin, in jeder Verhandlungssituation ein solches Verhandlungsergebnis zu finden. Ist
ein Verhandlungsergebnis. Der i-te Spieler erhält die Auszahlung xi. Das Verhandlungsproblem besteht darin, in jeder Verhandlungssituation ein solches Verhandlungsergebnis zu finden. Ist 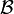 die Menge aller Verhandlungssituationen, so definieren wir daher:
die Menge aller Verhandlungssituationen, so definieren wir daher:Eine Verhandlungslösung ist eine Funktion
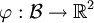 mit
mit 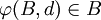 für alle
für alle 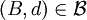 .
.Eigenschaften von Verhandlungslösungen
Natürlich wird man von einer Verhandlungslösung gewisse Eigenschaften fordern, die die Lösung als „vernünftig“ erscheinen lässt. So ist die Verhandlungslösung φ(B,d): = d für alle
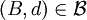 sicher nicht sehr „vernünftig“, da kein Spieler durch die Verhandlung mehr erhält als er sich ohnehin sichern könnte. Es geht daher im Folgenden darum, sinnvolle Eigenschaften zu finden, mit dem Ziel, dadurch in jeder Verhandlungssituation einen eindeutigen Auszahlungspunkt festzulegen.
sicher nicht sehr „vernünftig“, da kein Spieler durch die Verhandlung mehr erhält als er sich ohnehin sichern könnte. Es geht daher im Folgenden darum, sinnvolle Eigenschaften zu finden, mit dem Ziel, dadurch in jeder Verhandlungssituation einen eindeutigen Auszahlungspunkt festzulegen.Pareto-Optimalität
Eine Verhandlungslösung
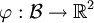 heißt Pareto-optimal, wenn es für keine Verhandlungssituation
heißt Pareto-optimal, wenn es für keine Verhandlungssituation 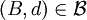 ein
ein 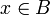 gibt mit
gibt mit 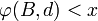 komponentenweise. D. h. es wird stets eine Verhandlungslösung gefunden, die keine gleichzeitige Besserstellung beider Parteien zulässt.
komponentenweise. D. h. es wird stets eine Verhandlungslösung gefunden, die keine gleichzeitige Besserstellung beider Parteien zulässt.Diese Bedingung ist mathematisch einleuchtend. In der Praxis mag es schwierig sein, solche nicht verbesserungsfähigen Verhandlungslösungen zu finden.
Symmetrie
Eine Verhandlungslösung φ heißt symmetrisch, falls folgendes gilt: Ist die Verhandlungssituation (B,d) symmetrisch, d. h. d1 = d2 und für alle
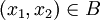 ist auch
ist auch 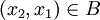 , so stimmen auch die Komponenten des Verhandlungsergebnisses φ(B,d) überein.
, so stimmen auch die Komponenten des Verhandlungsergebnisses φ(B,d) überein.Damit wird gefordert, dass sich die Verhandlungslösung in einer vollkommen symmetrischen Situation nicht ändert, wenn die Spieler ihre Rollen tauschen. Beiden Spielern wird gleiches Verhandlungsgeschick unterstellt.
Unabhängigkeit von positiven linearen Transformationen
Wir betrachten positive lineare Transformationen
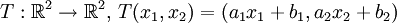 mit a1 > 0,a2 > 0. T bedeutet für beide Komponenten eine Skalenänderung zusammen mit einer Verschiebung. Eine Verhandlungslösung
mit a1 > 0,a2 > 0. T bedeutet für beide Komponenten eine Skalenänderung zusammen mit einer Verschiebung. Eine Verhandlungslösung 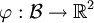 heißt unabhängig von positiven linearen Transformationen, falls für jede positive lineare Transformation T und jede Verhandlungssituation (B,d) gilt, dass
heißt unabhängig von positiven linearen Transformationen, falls für jede positive lineare Transformation T und jede Verhandlungssituation (B,d) gilt, dass 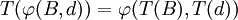 .
.Die Forderung nach Unabhängigkeit von positiven linearen Transformationen ist mathematisch sehr naheliegend und für viele mathematische Überlegungen auch unabdingbar. Für die Praxis bedeutet das, dass die Verhandlungen unabhängig vor der Skalengröße der Verhandlungsmasse verlaufen. Da Verhandlungen Zeit und Ressourcen kosten, kann man für die Praxisrelavanz dieser Forderung Bedenken anmelden.
Unabhängigkeit von irrelevanten Alternativen
Eine Verhandlungslösung
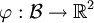 heißt unabhängig von irrelevanten Alternativen, wenn für zwei Verhandlungssitationen
heißt unabhängig von irrelevanten Alternativen, wenn für zwei Verhandlungssitationen 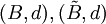 mit
mit 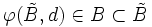 stets
stets 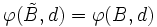 gilt.
gilt.Diese Forderung erscheint naheliegend, besagt sie doch, dass eine in der größeren Verhandlungsmenge
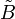 gefundene Lösung, die bereits in der kleineren Verhandlungsmenge B liegt, auch die Lösung für die kleinere Verhandlungsmenge sein wird, denn selbst in der größeren Verhandlungsmenge kann man nichts besseres finden. Gegen diese Forderung lassen sich wohl nur psychologische Einwände erheben: eine veränderte Verhandlungssituation ändert das Verhandlungsverhalten.
gefundene Lösung, die bereits in der kleineren Verhandlungsmenge B liegt, auch die Lösung für die kleinere Verhandlungsmenge sein wird, denn selbst in der größeren Verhandlungsmenge kann man nichts besseres finden. Gegen diese Forderung lassen sich wohl nur psychologische Einwände erheben: eine veränderte Verhandlungssituation ändert das Verhandlungsverhalten.Monotonie
Für eine Verhandlungssituation (B,d) sei
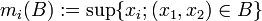 die maximale Auszahlung, die für den i-ten Spieler überhaupt möglich wäre. Eine Verhandlungslösung
die maximale Auszahlung, die für den i-ten Spieler überhaupt möglich wäre. Eine Verhandlungslösung 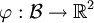 heißt monoton, falls für
heißt monoton, falls für 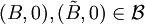 mit
mit 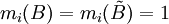 für i=1,2 und
für i=1,2 und 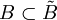 stets komponentenweise
stets komponentenweise 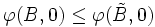 folgt.
folgt.Wenn sich also beide Spieler nur den Betrag 0 sichern können und beide maximal die Auszahlung 1 erzielen können, so sollte sich für keinen Spieler eine Veschlechterung ergeben, wenn man unter Beibehaltung dieser Bedingungen von einer kleineren Verhandlungsmenge zu einer größeren übergeht.
Existenz und Eindeutigkeitssätze
Die Nash’sche Verhandlungslösung
Satz von Nash: Es gibt genau eine Pareto-optimale, symmetrische, von positiven lineraren Transformationen unabhängige und von irrelavanten Alternativen unabhängige Verhandlungslösung.
Wenn zwei Spieler die hier genannten vier Forderungen an eine Verhandlungslösung akzeptieren, dann gibt es also in jeder Verhandlungssituation eine eindeutige Verhandlungslösung, diese nennt man die Nash’sche Verhandlungslösung. Diese Verhandlungslösung kann wie folgt ermittelt werden: Ist (B,d) eine Verhandlungssituation, so nimmt die Funktion
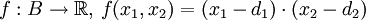 in genau einem Punkt aus B das Maximum an, und dieser Punkt ist die Nash’sche Verhandlungslösung.
in genau einem Punkt aus B das Maximum an, und dieser Punkt ist die Nash’sche Verhandlungslösung.Die Nash’sche Verhandlungslösung ist nicht monoton!
Die monotone Verhandlungslösung
Satz von Kalai-Smorodinsky: Es gibt genau eine Pareto-optimale, symmetrische, von positiven linearen Transformationen unabhängige und monotone Verhandlungslösung.
Diese Lösung nennt man die monotone Verhandlungslösung. Zur Ermittlung der monotonen Verhandlungslösung bestimmt man zu einer gegebenen Verhandlungssituation (B,d) eine positive lineare Transformation T, so dass T(d) = 0 und m1(T(B)) = m2(T(B)) = 1. Auf der Geraden
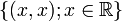 gibt es einen bzgl. der komponentenweisen Ordnung größten Punkt
gibt es einen bzgl. der komponentenweisen Ordnung größten Punkt 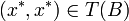 . Das gesuchte Verhandlungsergebnis ist dann T − 1(x * ,x * ).
. Das gesuchte Verhandlungsergebnis ist dann T − 1(x * ,x * ).Verhandlungslösung des Gefangenendilemmas
In der Situation des Gefangenendilemmas besteht die Menge der möglichen gemeinsamen Auszahlungen mit den oben genannten Zahlen aus den vier Punkten (-8,-8),(0,-10),(−10,0) und (-1,-1). Die konvexe Hülle ist das von diesen Punkten erzeugte Viereck. Der Garantiepunkt ist d=(-8,-8). Über nicht grau schattierte Punkte nebenstehender Zeichnung gibt es nichts zu verhandeln, der grau schattierte Bereich ist also die Verhandlungsmenge B. Beide Lösungskonzepte, die Nash’sche und die monotone Verhandlungslösung, führen auf (-1,-1) als Lösung.
Verhandlungslösung in der Praxis
Um neben theoretischen und mathematischen Beiträgen eine Vorstellung der Verhandlungslösung in Praxis-Situationen erhalten zu können, werden nachfolgend zwei Beispiele erläutert.
Lösungsfindung im Geschäftsleben
Betrachtet wird ein Hotel in einem Sommerbadeort. Der Sachverhalt besteht aus zwei Parteien – dem Hotelmanagement und der Gewerkschaft. Beide Parteien befinden sich am Anfang einer Lohnverhandlung. Wenn sich das Hotel in Betrieb befindet, macht es 1000 Dollar Gewinn pro Tag. Die Dauer der Saison beträgt 101 Tage.
Die Verhandlungen beginnen, indem die Gewerkschaft ein erstes Angebot an das Hotelmanagement richtet. Lehnt dieses das Angebot ab, gibt es am nächsten Tag ein Gegenangebot ab. Die Eröffnung des Hotels kann erst dann erfolgen, wenn eine Einigung erreicht ist. Diese entspricht der Verhandlungslösung.
Die Verhandlungen ziehen sich nun so lange hin, dass das Hotel bei einer Einigung in der nächsten Runde nur noch den letzten Tag der Saison geöffnet haben kann. An diesem letztmöglichen Tag der Angebotsabgabe ist die Gewerkschaft an der Reihe, ein Angebot zu abzugeben. Das Hotelmanagement sollte an diesem Punkt jeden Vorschlag akzeptieren, da sonst beide Parteien leer ausgehen. Die Gewerkschaft könnte also den kompletten Gewinn von 1000 Dollar für sich beanspruchen – theoretisch. Praktisch würde sich das Hotelmanagement nicht mit 0 Dollar zufrieden geben. Das heißt, die Gewerkschaft müsste dem Hotelmanagement wenigstens einen Mindestanteil zugestehen, beispielsweise 100 Dollar.
Dieses Beispiel zeigt, dass um zu einer für alle Parteien befriedigenden Verhandlungslösung zu kommen, man vorausschauend handeln sollte. Das heißt, dass schon zu Anfang einer Verhandlung bereits das Ende betrachtet werden sollte. Hätten sich die Parteien im Sachverhalt des Hotels bereits am Anfang das Ende der Verhandlung vor Augen geführt, wären nicht die Verluste der ersten 100 Tage entstanden.
Lösungsfindung in Kriegssituationen
Um eine Verhandlungslösung finden zu können, kann durch spieltheoretische Ansätze die bestmögliche Strategie ermittelt werden und somit zum Verhandlungserfolg für beide Seiten führen.
Das Santa Fee Institute in New Mexico hat ein Modell entwickelt, welches Bürgerkriegsparteien helfen soll, eine für beide Seiten gerechte Verhandlungslösung zu finden. Handelt es sich beispielsweise um zwei Parteien, welche das gleiche Territorium für sich beanspruchen, so muss dieses anhand einer Formel so geteilt werden, dass bei beiden Parteien Zufriedenheit und Unzufriedenheit gleich groß sind.
Die Funktionsweise des entwickelten Modells besteht darin, Friedens-Hindernisse zu erfassen und Auswege dafür aufzuzeigen. Hierbei ist es bedeutsam, dass sich beide Parteien von der Alles-oder-Nichts-Haltung trennen, dass eine faire Aufteilung stattfinden kann.
Kritisch an diesem Modell ist die Möglichkeit zu betrachten, dass eine der beiden Parteien im Nachhinein doch noch versuchen könnte, sein ihm zugestandenes Gebiet auf Kosten der anderen Partei vergrößern zu wollen. Weiterhin zeigten Erfahrungen mit spieltheoretischen Modellen bereits in den Jahren 1970 bis 1980, dass keine der Parteien Risiken eingehen möchte. Diesen Sachverhalt stellten Spieltheoretiker anhand des amerikanischen und sowjetischen Militärs fest, als es um die Frage ging, wie viele Raketen von den entsprechenden Parteien gebaut werden sollten. Letztlich gaben Mathematiker die Empfehlung, lieber ein paar mehr Raketen als notwendig zu bauen.
Abschließende Bemerkungen
- Häufig liest man von der Forderung der individuellen Rationalität, wonach das Verhandlungsergebnis stets komponentenweise nicht schlechter als der Garantiepunkt sein darf. In der hier gegebenen Darstellung steckt diese Forderung bereits in der Definition der Verhandlungssituation.
- Zur Monotonie hätte man allgemeiner fordern können, dass sich in jeder Verhandlungssituation die Situation für beide Spieler nur verbessern kann, wenn man die Verhandlungsmenge B unter sonst gleichen Bedingungen vergrößert. Es zeigt sich, dass diese Forderung so stark ist, dass sie keine Verhandlungslösung mehr zulässt.
- Bei der monotonen Verhandlungslösung ist gegenüber der Nash’schen Verhandlungslösung lediglich die Unabhängigkeit von irrelevanten Alternativen durch die Monotonieforderung ersetzt worden.
- Die Nash’sche und die monotone Verhandlungslösung stimmen in symmetrischen Verhandlungssituationen überein, wie z. B. im Gefangenendilemma.
Literatur
- J. F. Nash: The bargaining problem, Econometrica 18 (1950), 155–162
- E. Kalai, M. Smorodinsky: Other solutions to Nash’s bargaining problem, Econometrica 45 (1977), 1623–1630
- B. Rauhut, N. Schmitz, E. W. Zachow: Spieltheorie, Teubner (1979)
- M. Holler, G. Illing: Einführung in die Spieltheorie, Springer (1996)
- A. K. Dixit, B. J. Nalebuff: Spieltheorie für Einsteiger, Schäffer-Poeschel (1997)
- spiegel.de, Artikel vom 16. Dezember 2003 (Suchbegriff: "Formeln sollen Frieden schaffen")
- Spieler 1:
Wikimedia Foundation.





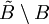 sind irrelevante Alternativen
sind irrelevante Alternativen
