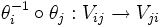- Semi-Riemannsche Mannigfaltigkeit
-
topologische Mannigfaltigkeit berührt die Spezialgebiete
ist Spezialfall von
- topologischer Raum
- parakompakter Hausdorff-Raum
- topologische Mannigfaltigkeit
- parakompakter Hausdorff-Raum
umfasst als Spezialfälle
- Euklidischer Raum
- Lie-Gruppe
- Riemannsche Mannigfaltigkeit
- Minkowski-Raum
- Pseudo-Riemannsche Mannigfaltigkeit
Eine Mannigfaltigkeit bezeichnet in der Mathematik einen topologischen Raum, der lokal dem euklidischen Raum
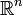 gleicht. Im Ganzen muss die Mannigfaltigkeit nicht einem Euklidischen Raum entsprechen (nicht zu ihm homöomorph sein).
gleicht. Im Ganzen muss die Mannigfaltigkeit nicht einem Euklidischen Raum entsprechen (nicht zu ihm homöomorph sein).Mannigfaltigkeiten sind der zentrale Gegenstand der Differentialgeometrie; sie haben bedeutende Anwendungen in der theoretischen Physik.
Inhaltsverzeichnis
Einführendes Beispiel
Ein gern gewähltes Beispiel für eine Mannigfaltigkeit ist eine Sphäre (= Kugeloberfläche), anschaulich etwa die Erdoberfläche:
Jede Region der Erde kann man mit einer Karte auf eine Ebene (
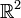 ) abbilden. Nähert man sich dem Rand der Karte, sollte man zu einer anderen Karte wechseln, die das angrenzende Gebiet darstellt. So kann man eine Mannigfaltigkeit durch einen vollständigen Satz von Karten vollständig beschreiben; man braucht dabei Regeln, wie sich beim Kartenwechsel die Karten überlappen. Dagegen gibt es keine einzelne Karte, auf der die gesamte Kugeloberfläche vollständig dargestellt werden kann, ohne sie zu „zerreißen“; Weltkarten haben ja auch stets „Ränder“, oder sie bilden Teile der Erde zweimal ab.
) abbilden. Nähert man sich dem Rand der Karte, sollte man zu einer anderen Karte wechseln, die das angrenzende Gebiet darstellt. So kann man eine Mannigfaltigkeit durch einen vollständigen Satz von Karten vollständig beschreiben; man braucht dabei Regeln, wie sich beim Kartenwechsel die Karten überlappen. Dagegen gibt es keine einzelne Karte, auf der die gesamte Kugeloberfläche vollständig dargestellt werden kann, ohne sie zu „zerreißen“; Weltkarten haben ja auch stets „Ränder“, oder sie bilden Teile der Erde zweimal ab.Die Dimension einer Mannigfaltigkeit entspricht der Dimension einer lokalen Karte; alle Karten haben die gleiche Dimension.
Übersicht
Wenn die Kartenwechsel hinreichend glatt sind, hat man eine differenzierbare Mannigfaltigkeit. Aus der Analysis bekannte Begriffe wie die Ableitung lassen sich auf natürliche Art auch auf differenzierbare Mannigfaltigkeiten übertragen. Eine riemannsche Mannigfaltigkeit besitzt mit der riemannschen Metrik – nach Bernhard Riemann – eine zusätzliche Struktur, die es erlaubt, Winkel und Entfernungen zu bestimmen.
Hinweis: Eine Sphäre ist eine riemannsche Mannigfaltigkeit, die in einen euklidischen Raum höherer Dimension eingebettet ist. Sie ist damit ein Beispiel für eine Untermannigfaltigkeit. Eine solche Einbettung existiert zwar für jede Mannigfaltigkeit (vgl. Einbettungssatz von Whitney und Einbettungssatz von Nash), die moderne mathematische Beschreibung von Mannigfaltigkeiten nimmt aber keinen Bezug auf einen Einbettungsraum.
In der Physik finden differenzierbare Mannigfaltigkeiten Verwendung als Phasenräume in der klassischen Mechanik und als vierdimensionale pseudo-Riemannsche Mannigfaltigkeiten zur Beschreibung der Raumzeit in der allgemeinen Relativitätstheorie und Kosmologie.
Arten von Mannigfaltigkeiten
Topologische Mannigfaltigkeiten
Sei M ein topologischer Raum. Man nennt M eine (topologische) Mannigfaltigkeit der Dimension n oder kurz eine n-Mannigfaltigkeit, falls die folgenden Eigenschaften erfüllt werden:
- M ist ein Hausdorff-Raum.
- M erfüllt das zweite Abzählbarkeitsaxiom.
- M ist lokal euklidisch, das heißt jeder Punkt besitzt eine Umgebung, welche homöomorph zu einer offenen Teilmenge des
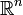 ist.
ist.
Mannigfaltigkeiten erben viele lokale Eigenschaften vom Euklidi'schen Raum: sie sind lokal wegzusammenhängend, lokal kompakt und lokal metrisierbar.
Mannigfaltigkeiten, welche homeomorph zueinander sind, werden als gleich (bzw. äquivalent) angesehen. Man interessiert sich nun dafür wie viele nicht äquivalente Mannigfaltigkeiten es gibt. Es ist jedoch nicht möglich, alle Mannigfaltigkeiten zu klassifizieren. Die zusammenhängenden 1-dimensionalen Mannigfaltigkeiten sind die reelle Zahlengerade
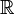 und der Kreis
und der Kreis 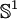 . Die Klassifikation der 2-Mannigfaltigkeiten ist ebenfalls bekannt. Die Geometrisierung von 3-Mannigfaltigkeiten stellt eine Klassifizierung derselben dar; ihr Beweis durch Grigori Perelman stellt einen der Höhepunkte der Mathematik im frühen 21. Jahrhundert dar. Die 4-dimensionalen Fälle können nicht klassifiziert werden (jede endlich-erzeugte Gruppe ist als Fundamentalgruppe eines solchen Raumes realisierbar, und eine Klassifizierung aller endlich-erzeugten Gruppen ist unmöglich).
. Die Klassifikation der 2-Mannigfaltigkeiten ist ebenfalls bekannt. Die Geometrisierung von 3-Mannigfaltigkeiten stellt eine Klassifizierung derselben dar; ihr Beweis durch Grigori Perelman stellt einen der Höhepunkte der Mathematik im frühen 21. Jahrhundert dar. Die 4-dimensionalen Fälle können nicht klassifiziert werden (jede endlich-erzeugte Gruppe ist als Fundamentalgruppe eines solchen Raumes realisierbar, und eine Klassifizierung aller endlich-erzeugten Gruppen ist unmöglich).Differenzierbare Mannigfaltigkeiten
Hauptartikel: Differenzierbare Mannigfaltigkeit
Um differenzierbare Funktionen zu betrachten, reicht die Struktur einer topologischen Mannigfaltigkeit nicht aus. Es sei M eine solche topologische n-Mannigfaltigkeit ohne Rand. Hat man eine offene Teilmenge von M, auf der ein Homöomorphismus zu einer offenen Menge von
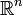 definiert ist, nennt man diesen Homöomorphismus eine Karte. Eine Menge von Karten, deren Urbilder M überdecken, nennt man einen Atlas von M. Verschiedene Karten θ,η induzieren einen Homöomorphismus
definiert ist, nennt man diesen Homöomorphismus eine Karte. Eine Menge von Karten, deren Urbilder M überdecken, nennt man einen Atlas von M. Verschiedene Karten θ,η induzieren einen Homöomorphismus 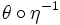 (einen so genannten Kartenwechsel oder Koordinatenwechsel) zwischen offenen Teilmengen von
(einen so genannten Kartenwechsel oder Koordinatenwechsel) zwischen offenen Teilmengen von 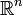 . Falls für einen Atlas
. Falls für einen Atlas 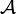 alle solchen Kartenwechsel k-mal differenzierbar sind, dann nennt man
alle solchen Kartenwechsel k-mal differenzierbar sind, dann nennt man 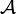 einen Ck-Atlas. Zwei Ck-Atlanten (derselben Mannigfaltigkeit) nennt man genau dann miteinander verträglich, wenn ihre Vereinigung wieder einen Ck-Atlas bildet. Diese Verträglichkeit ist eine Äquivalenzrelation. Eine Ck-Mannigfaltigkeit ist eine topologische Mannigfaltigkeit zusammen mit einem Ck-Atlas (eigentlich mit einer Äquivalenzklasse von Ck-Atlanten). Glatte Mannigfaltigkeiten sind Mannigfaltigkeiten vom Typ
einen Ck-Atlas. Zwei Ck-Atlanten (derselben Mannigfaltigkeit) nennt man genau dann miteinander verträglich, wenn ihre Vereinigung wieder einen Ck-Atlas bildet. Diese Verträglichkeit ist eine Äquivalenzrelation. Eine Ck-Mannigfaltigkeit ist eine topologische Mannigfaltigkeit zusammen mit einem Ck-Atlas (eigentlich mit einer Äquivalenzklasse von Ck-Atlanten). Glatte Mannigfaltigkeiten sind Mannigfaltigkeiten vom Typ 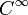 . Sind alle Kartenwechsel sogar analytisch, dann nennt man die Mannigfaltigkeit ebenfalls analytisch oder auch Cω-Mannigfaltigkeit.
. Sind alle Kartenwechsel sogar analytisch, dann nennt man die Mannigfaltigkeit ebenfalls analytisch oder auch Cω-Mannigfaltigkeit.Auf einer Ck-Mannigfaltigkeit M nennt man eine Funktion
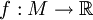 genau dann s-mal differenzierbar (
genau dann s-mal differenzierbar (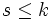 ), wenn sie auf jeder Karte s-mal differenzierbar ist.
), wenn sie auf jeder Karte s-mal differenzierbar ist.Zu jeder (parakompakten) Cr-Mannigfaltigkeit (r > 1) existiert ein Atlas, der beliebig oft differenzierbar oder sogar analytisch ist. In der Tat ist diese Struktur sogar eindeutig, d.h. es ist keine Einschränkung der Allgemeinheit anzunehmen, dass jede Mannigfaltigkeit analytisch ist (wenn man von differenzierbaren Mannigfaltigkeiten redet).
Diese Aussage ist aber für topologische Mannigfaltigkeiten der Dimension 4 oder höher nicht mehr unbedingt richtig: So gibt es sowohl C0-Mannigfaltigkeiten, die keine differenzierbare Struktur besitzen, als auch C1-Mannigfaltigkeiten (oder auch Cω-M., s.o.), die als differenzierbare Mannigfaltigkeiten unterschiedlich, aber als topologische Mannigfaltigkeiten gleich sind. Das bekannteste Beispiel für den zweiten Fall sind die so genannten exotischen 7-Sphären, die alle homöomorph zu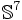 (aber untereinander nicht diffeomorph) sind. Da die topologische und die differenzierbare Kategorie in niedriger Dimension übereinstimmen, sind solche Resultate leider nur schwer zu veranschaulichen.
(aber untereinander nicht diffeomorph) sind. Da die topologische und die differenzierbare Kategorie in niedriger Dimension übereinstimmen, sind solche Resultate leider nur schwer zu veranschaulichen.Tangentialbündel
An jedem Punkt p einer n-dimensionalen, differenzierbaren (aber nicht einer topologischen) Mannigfaltigkeit findet man einen Tangentialraum. In einer Karte heftet man an diesen Punkt einfach einen
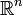 an und überlegt sich dann, dass das Differential eines Koordinatenwechsels an jedem Punkt einen linearen Isomorphismus definiert, der die Transformation des Tangentialraums in die andere Karte leistet. Abstrakt definiert man den Tangentialraum an p entweder als den Raum der Derivationen an diesem Punkt oder den Raum von Äquivalenzklassen von differenzierbaren Kurven (wobei die Äquivalenzrelation angibt, wann die Geschwindigkeitvektoren zweier Kurven an p gleich sein sollen).
an und überlegt sich dann, dass das Differential eines Koordinatenwechsels an jedem Punkt einen linearen Isomorphismus definiert, der die Transformation des Tangentialraums in die andere Karte leistet. Abstrakt definiert man den Tangentialraum an p entweder als den Raum der Derivationen an diesem Punkt oder den Raum von Äquivalenzklassen von differenzierbaren Kurven (wobei die Äquivalenzrelation angibt, wann die Geschwindigkeitvektoren zweier Kurven an p gleich sein sollen).Die Vereinigung aller Tangentialräume einer Mannigfaltigkeit bildet ein Vektorbündel, das Tangentialbündel genannt wird. Der Tangentialraum einer Mannigfaltigkeit M im Punkt p wird meist mit TpM bezeichnet, das Tangentialbündel mit TM.
Ein Unterbündel des Tangentialbündels ist das Einheitstangentialbündel UTM, das nur aus Tangentialvektoren der Länge 1 besteht. Seine Fasern sind keine Vektorräume, sondern Sphären der Dimension n − 1. Daher ist es kein Vektorbündel sondern nur ein Faserbündel. Als Bündel ist es unabhängig von der Wahl der Metrik auf den Tangentialräumen.
Komplexe Mannigfaltigkeiten
Hauptartikel: Komplexe Mannigfaltigkeit
Eine topologische Mannigfaltigkeit X heißt komplexe Mannigfaltigkeit der (komplexen) Dimension n, falls jeder Punkt
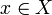 eine offene Umgebung
eine offene Umgebung 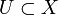 hat, die homöomorph zu einer offenen Menge
hat, die homöomorph zu einer offenen Menge  ist. Ferner fordert man, dass für je zwei Karten
ist. Ferner fordert man, dass für je zwei Karten  der Kartenwechsel
der Kartenwechselholomorph ist. Hierbei bezeichne
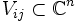 die Menge
die Menge 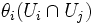 .
.Der wesentliche Unterschied zu gewöhnlichen differenzierbaren Mannigfaltigkeiten liegt weniger im Unterschied zwischen
 und
und 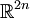 , sondern in der viel stärkeren Forderung der komplexen Differenzierbarkeit der Kartenwechselabbildungen.
, sondern in der viel stärkeren Forderung der komplexen Differenzierbarkeit der Kartenwechselabbildungen.(Zusammenhängende) Komplexe Mannigfaltigkeiten der Dimension 1 werden als Riemannsche Flächen bezeichnet. Andere spezielle komplexe Mannigfaltigkeiten sind die Kählermannigfaltigkeit, welche eine komplexe, riemannsche Mannigfaltigkeit ist, und die steinsche Mannigfaltigkeit.
Semi-Riemannsche Mannigfaltigkeiten
Auf einer "nackten" differenzierbaren Mannigfaltigkeit ist es nicht möglich, Abstände, Winkel oder Volumen zu bestimmen. Semi-Riemannsche Mannigfaltigkeiten (auch Pseudo-Riemannsche Mannigfaltigkeiten genannt) sind spezielle differenzierbare Mannigfaltigkeiten. Hier gibt es als sogenannte Metrik nicht unbedingt ein (positiv definites) Skalarprodukt, sondern nur eine symmetrische, nicht-ausgeartete Bilinearform. Mit dieser lassen sich Abstände, Winkel und Volumen definieren, wobei diese Begriffe jedoch nicht immer der anschaulichen Interpretation dieser Worte entsprechen.
Nach dem Trägheitssatz von Sylvester lässt sich eine solche Bilinearform in einer Orthonormalbasis als Diagonalmatrix mit Einträgen von
 darstellen. Sind dann r Einträge +1 und s Einträge -1, spricht man von einer Metrik mit Signatur (r, s).
darstellen. Sind dann r Einträge +1 und s Einträge -1, spricht man von einer Metrik mit Signatur (r, s).Ist die Signatur der Metrik (1,m − 1), wobei m die Dimension der Mannigfaltigkeit ist, spricht man von einer Lorentz-Mannigfaltigkeit.
Riemannsche Mannigfaltigkeiten
Hauptartikel: Riemannsche Mannigfaltigkeit
Will man Abstände, Winkel und Volumen so definieren, dass die Definition mit dem anschaulichen Verständnis dieser Begriffe übereinstimmt, so ist die üblichste Art, alle diese Größen festzulegen, die Angabe eines Skalarproduktes des Tangentialraums an jedem Punkt der Mannigfaltigkeit (oder äquivalent einer orthonormalen Basis von Tangentialvektoren).
Eine solche Mannigfaltigkeit nennt man dann Riemannsche Mannigfaltigkeit. Riemannsche Mannigfaltigkeiten sind also Semi-Riemannsche Mannigfaltigkeiten, deren Metriken Skalarprodukte sind, also die Signatur (m,0) haben, wobei m die Dimension der Mannigfaltigkeit ist.
Besteht nur die Forderung nach einer Längenmessung, gibt es die allgemeineren Finslerschen Mannigfaltigkeiten (auch Finsler-Geometrie).
Eigenschaften
- Jede Mannigfaltigkeit hat eine abzählbare Fundamentalgruppe.
- Jede Mannigfaltigkeit der Dimension
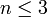 ist triangulierbar. Vierdimensionale Mannigfaltigkeiten sind nicht triangulierbar und es ist immer noch (April 2009) unbekannt, ob Mannigfaltigkeiten höherer Dimension triangulierbar sind.
ist triangulierbar. Vierdimensionale Mannigfaltigkeiten sind nicht triangulierbar und es ist immer noch (April 2009) unbekannt, ob Mannigfaltigkeiten höherer Dimension triangulierbar sind.
Ränder, Orientierung
Eine Sphäre (=Kugeloberfläche) ist eine Mannigfaltigkeit ohne Rand. Eine Vollkugel dagegen ist eine Mannigfaltigkeit mit Rand; ihr Rand ist gerade die Kugeloberfläche. Hierbei soll auf eine technische Definition des Begriffs Rand (boundary) verzichtet und darauf hingewiesen werden, dass die im folgenden gegebene Definition des Begriffs Mannigfaltigkeit nur Mannigfaltigkeiten ohne Ränder einschließt.
Mannigfaltigkeiten können orientierbar sein. Bekannteste Beispiele nicht-orientierbarer Mannigfaltigkeiten sind etwa das Möbiusband und die kleinsche Flasche. Auch solche Mannigfaltigkeiten sollen im weiteren nicht betrachtet werden.
Lie-Gruppen
Eine Lie-Gruppe G ist sowohl eine differenzierbare Mannigfaltigkeit als auch eine Gruppe. Man fordert, dass beide Strukturen miteinander verträglich sind. Diese Objekte beschreiben typische Symmetrien von geometrischen Strukturen und physikalischen Systemen.
Der Tangentialraum einer Lie-Gruppe am Eins-Element ist die zugehörige Lie-Algebra.
Weblinks
Literatur
- John M. Lee: Introduction to Smooth Manifolds, Springer-Verlag, 2. Aufl. New York, 2003, ISBN 0-387-95448-1
- John M. Lee: Introduction to Topological Manifolds, Springer-Verlag, New York, ISBN 0-387-98759-2
- topologischer Raum
Wikimedia Foundation.