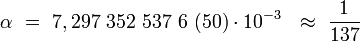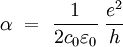Sommerfeldsche Feinstrukturkonstante

Die Feinstrukturkonstante α ist eine dimensionslose physikalische Konstante, die die Stärke der elektromagnetischen Wechselwirkung angibt. Sie wurde 1916 von Arnold Sommerfeld zur Beschreibung der Aufspaltung (Feinstruktur) von Spektrallinien im Spektrum des Wasserstoffatoms eingeführt, daher wird sie oft auch Sommerfeldkonstante oder Sommerfeldsche Feinstrukturkonstante genannt.

Ihr derzeit allgemein empfohlener Wert beträgt nach CODATA 2006^[1][2]

$\alpha\ =\ 7,297 \ 352 \ 537 \ 6 \ (50) \cdot 10^{-3} \ \ \approx \ \frac{1}{137}$

Sie hängt mit der Elementarladung e und dem Planckschem Wirkungsquantum h über die Vakuum-Lichtgeschwindigkeit c₀ und der elektrische Feldkonstanten ε₀ nach

$\alpha\ =\ \frac{1}{2 c_0 \varepsilon_0}\;\frac{e^2}{h}$

zusammen.

Die Feinstrukturkonstante ist die elektromagnetische Kopplungskonstante, das heißt sie beschreibt die Wahrscheinlichkeit, dass ein Austauschteilchen der elektromagnetischen Wechselwirkung, ein Photon, an ein elektrisch geladenes Elementarteilchen, zum Beispiel ein Elektron, koppelt. Damit bestimmt die Feinstrukturkonstante die Rate für physikalische Prozesse wie die Lichtemission und die Stärke der abstoßenden oder anziehenden Kräfte zwischen elektrisch geladenen Teilchen.

Vergleich der Grundkräfte

Direkt kann die elektromagnetische Wechselwirkung nur mit der Gravitation verglichen werden, da beide Kräfte dem gleichen Abstandsgesetz gehorchen. Genauer gesagt nimmt bei beiden Wechselwirkungen die Stärke der Kraft mit dem Quadrat des Abstandes ab.^[3]

Drückt man die durch die Gravitationskonstante angegebene Stärke der Gravitation zwischen zwei Protonen, also schwereren Elementarteilchen (im Vergleich z.B. zu Elektronen), in einer wie die Feinstrukturkonstante dimensionslosen Zahl aus, so erhält man einen Wert von

$\alpha_G\ =\ 5{,}9\;\cdot\;10^{-39}$.

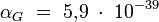Vergleicht man diesen Wert mit der Feinstrukturkonstanten, die die Stärke der elektrischen Abstoßung zwischen beiden angibt, so sieht man, dass die Gravitation etwa 10³⁶ mal schwächer ist als die elektromagnetische Wechselwirkung.

Die Starke Wechselwirkung hat eine 'laufende Kopplungskonstante'. Der Vergleichswert für die Kraft zwischen zwei Nukleonen im Atomkern ist

$\alpha_s\ \cong\ 1$.

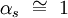Vergleicht man die Zerfallsraten aus starken und schwachen Zerfällen, so erhält man für die Schwache Kraft eine Kopplungskonstante von

$\alpha_w\ =\ 10^{-7}\ -\ 10^{-6}$.

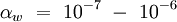Zeitliche Entwicklung

Die Frage, ob die Feinstrukturkonstante zeitlich variiert oder seit dem Urknall unverändert ist, ist von beträchtlichem theoretischem Interesse. Ob sie variiert, ist völlig unbekannt, bisherige Messungen konnten keine Veränderung eindeutig nachweisen.

Experimente und Messungen hierzu werden auf ganz unterschiedlichen Zeitskalen durchgeführt^[4][5]:

• Laborexperimente, u.a. mit Atomuhren, können die relative zeitliche Veränderung von α auf höchstens etwa 10^-16/Jahr einschränken.^[6][7]
• Die Beobachtung von Absorptionslinien von Quasaren verbessert diese Genauigkeit um ein bis zwei Größenordnungen^[8], wobei die Behandlung systematischer Fehler aber schwierig ist und bislang sowohl signifikant positive als auch Nullresultate publiziert wurden. Eine abschließende Auswertung aller Daten steht derzeit aus.
• Die Betrachtung der primordialen Nukleosynthese dehnt das Nullresultat auf Zeiten unmittelbar nach dem Urknall aus, allerdings mit größerem Fehlerbalken.
• Der Naturreaktor Oklo^[9] und die Isotopenverteilung in Meteoriten wurden ebenfalls für Abschätzungen benutzt.

Zitate

It has been a mystery ever since it was discovered more than fifty years ago, and all good theoretical physicists put this number up on their wall and worry about it. (Seit sie vor über fünfzig Jahren entdeckt wurde, ist sie ein Mysterium, und alle guten theoretischen Physiker hängen sich diese Zahl an die Wand und zerbrechen sich den Kopf darüber.) Richard P. Feynman, QED – The strange theory of light and matter, Princeton University Press 1985, p. 129

Quellen

1. ↑ CODATA Internationally recommended values of the Fundamental Physical Constants 2006
2. ↑ http://physics.nist.gov/cgi-bin/cuu/Value?alph
3. ↑ Rohlf, James William: Modern Physics from a to Z0, Wiley, 1994
4. ↑ John D. Barrow, Varying Constants, Phil.Trans.Roy.Soc.Lond. A363 (2005) 2139–2153, online
5. ↑ Jean-Philippe Uzan, The fundamental constants and their variation: observational status and theoretical motivations, Rev.Mod.Phys. 75 (2003) 403, online
6. ↑ M. Fischer et al, New Limits to the Drift of Fundamental Constants from Laboratory Measurements, Phys. Rev. Lett. 92, 230802 (2004), online
7. ↑ SG Karshenboim, E Peik, B Lipphardt, H Schnatz, T Schneider, Chr. Tamm, Limit on the Present Temporal Variation of the Fine Structure Constant, Phys. Rev. Lett. 93, 170801 (2004), online
8. ↑ R. Quast, D. Reimers, S. A. Levshakov, Probing the variability of the fine-structure constant with the VLT/UVES, Astron.Astrophys. 415 (2004) L7, online
9. ↑ Yasunori Fujii, Oklo Constraint on the Time-Variability of the Fine-Structure Constant, to be published in Lecture Notes in Physics, online

Siehe auch

Physikalische Konstanten