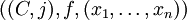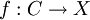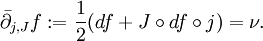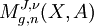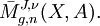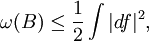- Stabile Abbildung (symplektische Topologie)
-
In der symplektischen Topologie kann man den Modulraum stabiler Abbildungen, von Riemannflächen in eine gegebene symplektische Mannigfaltigkeit definieren. Dieser Modulraum ist wesentlich für die Konstruktion der Gromov-Witten-Invarianten, die in der abzählenden algebraischen Geometrie und der Stringtheorie Anwendung finden.
Der Artikel ist eine Auslagerung des Artikels Gromov-Witten-Invariante, um diesen nicht zu sehr aufzublähen.
Inhaltsverzeichnis
Der Modulraum pseudoholomorpher Kurven
X sei eine geschlossene symplektische Mannigfaltigkeit mit der symplektischen Formω. g und n seien natürliche Zahlen einschließlich Null und A eine zweidimensionale Homologieklasse in X. Dann kann man die Menge der pseudoholomorphen Kurven
betrachten, wobei (C,j) eine glatte, geschlossene Riemannsche Fläche des Geschlechts g mit n markierten (ausgezeichneten) Punkten
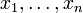 ist, und
ist, undeine Funktion ist, die für die Wahl einer bestimmten ω-zahmen (tame) fast komplexen Struktur J und inhomogenem Termν, die gestörten Cauchy-Riemann-Differentialgleichungen
erfüllt. Typischerweise erlaubt man nur solche g und n, die die punktierte Euler-Poincare-Charakteristik 2 − 2g − n von C negativ machen. Dann ist das Gebiet stablil, das heißt es gibt nur eine endliche Zahl von Automorphismen von C, die die markierten Punkte erhalten.
Der Operator
 ist ein elliptischer Operator und daher vom Fredholm Typ. Nach beträchtlicher analytischer Arbeit[1] kann man zeigen, dass für eine generische Wahl des ω-zahmen J und der Störung ν die Menge der (j,J,ν)-holomorphen Kurven vom Geschlecht g mit n markierten Punkten, die die Klasse A darstellen, ein glatter, orientierter Orbifold
ist ein elliptischer Operator und daher vom Fredholm Typ. Nach beträchtlicher analytischer Arbeit[1] kann man zeigen, dass für eine generische Wahl des ω-zahmen J und der Störung ν die Menge der (j,J,ν)-holomorphen Kurven vom Geschlecht g mit n markierten Punkten, die die Klasse A darstellen, ein glatter, orientierter Orbifoldist, mit einer Dimension, die durch das Atiyah-Singer-Indextheorem gegeben ist:
Die Kompaktifizierung der stabilen Abbildungen
Dieser Modulraum ist nicht kompakt, da eine Folge von Kurven in eine singuläre Kurve entarten kann, die dann außerhalb des bisher definierten Modulraums liegen würde. Das passiert z. B., wenn sich die Energie von f (gemeint ist die L2-Norm der Ableitung) in einem Punkt des Definitionsgebietes der Funktion (im Folgenden kurz Gebiet genannt) konzentriert. Man kann die Energie durch Reskalierung der Abbildung um den Konzentrationspunkt „einfangen“, wobei bildlich eine Sphäre (bubble, Blase, genannt) an das Gebiet angehängt wird und die Abbildung auf diese Blase ausgedehnt wird. Dabei können weitere Konzentrationspunkte erzeugt werden, so dass man iterativ vorgehen muss und dabei einen ganzen Bubble-Baum erzeugt.
Um das Ganze exakter zu formulieren definiert man eine stabile Abbildung als pseudoholomorphe Abbildung von einer Riemannfläche mit im schlimmsten Fall Knoten-Singularitäten, so dass es nur endlich viele Automorphismen der Abbildung gibt. Eine glatte Komponente einer Riemannfläche mit Knoten wird stabil genannt, wenn es nur endlich viele Automorphismen gibt, die die Knotenpunkte und markierten PUnkte erhalten. Eine stabile Abbildung ist eine pseudoholomorphe Abbildung mit wenigstens einer stabilen Gebietskomponente, so dass für alle anderen Gebietkomponenten die Abbildung nicht-konstant ist oder die Komponente stabil ist.
Das Gebiet einer stabilen Abbildung muss keine stabile Kurve sein, aber man kann seine instabilen Komponenten iterativ kontrahieren und so eine stabile Kurve erzeugen, die die Stabilisierung st(C) des Gebietes C genannt wird.
Die Menge aller stabilen Abbildungen von Riemannflächen des Geschlechts g mit n markierten Punkte bildet einen Modulraum
Die Topologie ist dadurch definiert, dass eine Folge stabiler Abbildungen dann und nur dann konvergent ist, wenn
- ihre (stabilisierten) Gebiete im Deligne-Mumford-Modulraum der Kurven
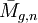 konvergieren,
konvergieren, - sie gleichmäßig in allen Ableitungen auf kompakten Untermengen außerhalb der Knoten konvergieren, und
- Die Energie-Konzentration in jedem Punkt gleich der Energie in jedem bubble-Baum ist, der diesem Punkt in der Grenz-Abbildung zugeordnet ist.
Der Modulraum der stabilen Abbildungen ist kompakt: jede Folge stabiler Abbildungen konvergiert gegen eine stabile Abbildung. Zum Beweis reskaliere man iterativ die Folge der Abbildungen. Jedes Mal erhält man im Grenzübergang ein neues Gebiet (möglicherweise singulär), mit wenger Energie-Konzentration als im Iterationsschritt davor. An dieser Stelle fließt das Vorhandensein einer symplektische Form ω in wesentlicher Weise ein. Die Energie jeder glatten Abbildung, die die Homologieklasse B darstellt, ist von unten durch die symplektische Fläche ω(B) begrenzt,
wobei das Gleichheitszeichen dann und nur dann gilt, falls die Abbildung pseudoholomorph ist. Das begrenzt die Energie, die in der Wiederholung der Reskalierung eingefangen wird und stellt sicher, dass nur endlich viele Reskalierungen nötig sind um die gesamte Energie einzufangen. Am Ende ist die Grenz-Abbildung auf dem neuen Grenz-Gebiet stabil.
Der kompaktifizierte Raum ist wieder ein glatter, orientierter Orbifold. Abbildungnen mit nicht-trivialen Automorphismen entsprechen Punkten auf dem Orbifold mit Isotropie.
Der Gromov-Witten-Pseudozyklus
Um Gromov-Witten-Invarianten zu konstruieren, führt man eine Ausführungsabbildung (evaluation map) im Modulraum der stabilen Abbildungen aus
um unter geeigneten Bedingungen eine rationale Homologieklasse zu bekommen:
Rationale Koeffizienten sind nötig, da der Modulraum ein Orbifold ist. Die durch die Ausführungsabbildung definierte Homologieklasse ist unabhängig von der Wahl des generischen ω-zahmen J und der Störung ν. Sie wird die Gromov-Witten-Invariante (GW) von X für gegebene g, n, und A genannt. Die Unabhängigkeit (bis auf Isotopie) der Homologieklasse von der Wahl von ω kann durch ein Kobordismus-Argument gezeigt werden. Die GW sind also Invariante von symplektischen Isotopieklassen symplektischer Mannigfaltigkeiten.
Die „geeigneten Bedingungen“ sind ziemlich technisch, hauptsächlich weil Abbildungen mit mehreren Blättern (einer Überlagerungsmannigfaltigkeit) größere Modulräume als erwartet bilden können. Die einfachste Vorgehensweise ist dann anzunehmen, dass die Zielmannigfaltigkeit der Abbildung X in einem bestimmten Sinn semipositiv (halbpositiv) oder eine Fano-Mannigfaltigkeit ist. Der Modulraum mehrfach-überdeckender Abbildungen hat dann mindestens Ko-Dimension 2 im Raum der einfach-überdeckenden Abbildungen. Das Bild der Ausführungsabbildung (evaluation map) bildet dann einen Pseudozyklus (pseudocycle), womit sich eine wohldefinierte Homologieklasse in der erwarteten Dimension definieren lässt. GW ohne eine Art Semipositivität verlangt eine schwierige technische Konstruktion, bekannt als Virtueller Modul-Zyklus (virtual moduli cycle).
Literatur
- Dusa McDuff und Dietmar Salamon, J-Holomorphic Curves and Symplectic Topology, American Mathematical Society colloquium publications, 2004. ISBN 0-8218-3485-1.
Einzelnachweise
- ↑ Vervollständigung eines geeigneten Sobolev-Raumes, Anwendung des Satz über implizite Funktionen, Sards Satz für Banachräume, Nutzung elliptischer Regularität um die Glattheit zurückzugewinnen.
Wikimedia Foundation.