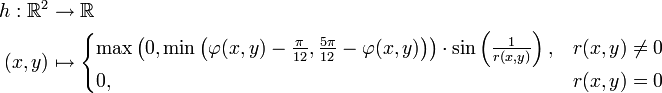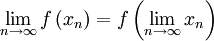- Stetigkeit (Mathematik)
-
Die Stetigkeit ist ein Konzept der Mathematik, das vor allem in den Teilgebieten der Analysis und der Topologie von zentraler Bedeutung ist. Eine Funktion heißt stetig, wenn verschwindend kleine Änderungen des Argumentes (der Argumente) nur zu verschwindend kleinen Änderungen des Funktionswertes führen. Das heißt insbesondere, dass in den Funktionswerten keine Sprünge auftreten. Treten Sprünge nur in einer Richtung auf, spricht man von Halbstetigkeit.
Inhaltsverzeichnis
- 1 Definitionen
- 2 Wichtige Sätze über stetige Funktionen
- 3 Differenzierbarkeit stetiger Funktionen
- 4 Funktionenräume stetiger Funktionen
- 5 Einzelnachweise
- 6 Weblinks
Definitionen
Die Idee der Stetigkeit kann wie folgt beschrieben werden: Eine reellwertige Funktion
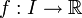 auf einem reellen Intervall
auf einem reellen Intervall 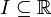 ist stetig, wenn der Graph der Funktion f ohne Absetzen des Stiftes gezeichnet werden kann. Die Funktion darf insbesondere keine Sprungstellen haben. Diese Aussage ist keine Definition, weil unklar ist, wie ohne Absetzen des Stiftes zeichnen in mathematischen Begriffen ausgedrückt werden könnte. Trotzdem entspricht sie ungefähr der Bedeutung der Stetigkeit und ist daher für die Anschauung sehr nützlich.
ist stetig, wenn der Graph der Funktion f ohne Absetzen des Stiftes gezeichnet werden kann. Die Funktion darf insbesondere keine Sprungstellen haben. Diese Aussage ist keine Definition, weil unklar ist, wie ohne Absetzen des Stiftes zeichnen in mathematischen Begriffen ausgedrückt werden könnte. Trotzdem entspricht sie ungefähr der Bedeutung der Stetigkeit und ist daher für die Anschauung sehr nützlich.Augustin Louis Cauchy und Bernard Bolzano gaben Anfang des 19. Jahrhunderts unabhängig voneinander eine Definition von Stetigkeit. Sie nannten eine Funktion stetig, wenn hinreichend kleine Änderungen des Arguments nur beliebig kleine Änderungen des Funktionswerts nach sich zögen. Dies war bereits eine exakte Definition, die aber in ihrer praktischen Anwendung gewisse Fragen offen lässt. Das heutzutage übliche ε-δ-Kriterium wurde von Karl Weierstraß am Ende des 19. Jahrhunderts eingeführt.
Es sagt in Worten etwa: Die Funktion f ist in einem Punkt p stetig, wenn es zu jeder Umgebung V seines Bildpunktes f(p) eine Umgebung U von p gibt, die durch f ganz in die Umgebung V abgebildet wird.
Zur Originaldefinition von Weierstraß:
Stetigkeit reeller Funktionen
Für reelle Funktionen – also Funktionen, deren Definitionsbereich und Zielbereich Teilmengen der reellen Zahlen sind – sind zwei äquivalente Definitionen der Stetigkeit üblich:
- Epsilon-Delta-Kriterium[1]:
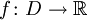 ist stetig in
ist stetig in 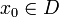 , wenn
, wenn
zu jedem ε > 0 ein δ > 0 existiert, so dass für alle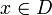 mit | x − x0 | < δ gilt:
mit | x − x0 | < δ gilt:  .
. - Folgenkriterium[2]:
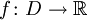 ist stetig in
ist stetig in 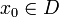 , wenn für jede Folge
, wenn für jede Folge 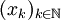 mit Elementen
mit Elementen 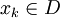 , die gegen x0 konvergiert, auch f(xk) gegen f(x0) konvergiert.
, die gegen x0 konvergiert, auch f(xk) gegen f(x0) konvergiert.
Eine Funktion heißt stetig in D, wenn sie an jeder Stelle ihres Definitionsbereiches stetig ist.
Der Begriff der Stetigkeit einer Funktion lässt sich auch mit Hilfe des Begriffs des Grenzwerts einer Funktion definieren: Eine Funktion f ist stetig in
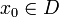 genau dann, wenn der Grenzwert von f für
genau dann, wenn der Grenzwert von f für 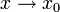 existiert und
existiert und  gilt oder wenn x0 ein isolierter Punkt ist.[3]
gilt oder wenn x0 ein isolierter Punkt ist.[3]Beispiele und Gegenbeispiele
- Die Sinusfunktion
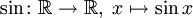 ist in
ist in  stetig.
stetig. - Die Kosinusfunktion
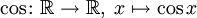 ist in
ist in  stetig.
stetig. 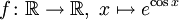 ist (als Komposition der Exponential- und der Kosinusfunktion) in
ist (als Komposition der Exponential- und der Kosinusfunktion) in  stetig.
stetig.- Die Tangensfunktion
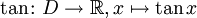 ist stetig in ihrem gesamten Definitionsbereich D. Dieser ergibt sich wegen
ist stetig in ihrem gesamten Definitionsbereich D. Dieser ergibt sich wegen 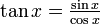 zu
zu 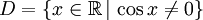 , also zu
, also zu  .
. - Die Kehrwert-Funktion
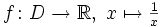 ist stetig in ihrem gesamten Definitionsbereich
ist stetig in ihrem gesamten Definitionsbereich 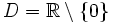 .
.
- Die Signum-Funktion
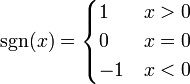
ist an jeder Stelle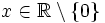 stetig, aber an der Stelle 0 unstetig: Der linksseitige Grenzwert ist −1, der rechtsseitige Grenzwert +1 und somit existiert der Grenzwert
stetig, aber an der Stelle 0 unstetig: Der linksseitige Grenzwert ist −1, der rechtsseitige Grenzwert +1 und somit existiert der Grenzwert  nicht. Deshalb ist die Signum-Funktion nicht auf ganz
nicht. Deshalb ist die Signum-Funktion nicht auf ganz  stetig.
stetig. - Die Funktion
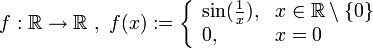
ist an der Stelle 0 unstetig (sogenannte Oszillationsstelle), in allen anderen Punkten stetig.ist an jeder Stelle unstetig.
Bemerkung: Keine Unstetigkeitsstellen sind die Argumente
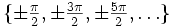 der Tangensfunktion sowie das Argument x = 0 der Kehrwert-Funktion, da die Funktionen an diesen Stellen gar nicht definiert sind und sich Stetigkeit immer nur auf Punkte des Definitionsbereichs beziehen kann.
der Tangensfunktion sowie das Argument x = 0 der Kehrwert-Funktion, da die Funktionen an diesen Stellen gar nicht definiert sind und sich Stetigkeit immer nur auf Punkte des Definitionsbereichs beziehen kann.Eigenschaften
- Sind f und g stetig auf einem gemeinsamen Definitionsbereich D, so sind auch f + g, f − g,
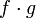 und
und  stetig; allerdings muss der Definitionsbereich von
stetig; allerdings muss der Definitionsbereich von  für den Fall, dass g eine oder mehrere Nullstellen hat, auf den Bereich
für den Fall, dass g eine oder mehrere Nullstellen hat, auf den Bereich 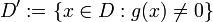 eingeschränkt werden.
eingeschränkt werden.
- Die Komposition
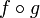 zweier stetiger Funktionen ist ebenfalls stetig.
zweier stetiger Funktionen ist ebenfalls stetig.
Linksseitige/rechtsseitige Stetigkeit
Eine auf einer Menge
 definierte Funktion f ist in einem Punkt
definierte Funktion f ist in einem Punkt 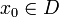 linksseitig stetig, wenn
linksseitig stetig, wenn  . Die Funktion ist also an der Stelle x0 linksseitig stetig, weil direkt links neben x0 kein Sprung (und auch keine anderweitige Unstetigkeit) liegt.
. Die Funktion ist also an der Stelle x0 linksseitig stetig, weil direkt links neben x0 kein Sprung (und auch keine anderweitige Unstetigkeit) liegt.Ist f stetig in x0, so ist f auch linksseitig stetig in x0. Ist f auf dem ganzen Definitionsbereich linksseitig stetig, so sagt man auch, f ist linksstetig.
Die Definition von rechtsseitig stetig ist völlig analog zur linksseitigen, nur muss hier der rechtsseitige Grenzwert betrachtet werden.
Eine auf einer Teilmenge der reellen Zahlen definierte Funktion ist also genau dann stetig in x0, wenn sie in x0 sowohl linksseitig als auch rechtsseitig stetig ist.
Verallgemeinerung: Stetige Funktionen zwischen metrischen Räumen
Eine Funktion heißt stetig, wenn sich ihr Funktionswert genügend wenig ändert, solange man nur das Funktionsargument genügend wenig ändert. Mit den Begriffen des metrischen Raumes lässt sich diese Beschreibung in verschiedener Weise formalisieren.
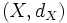 und
und 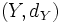 sind jeweils metrische Räume mit den zugehörigen Metriken,
sind jeweils metrische Räume mit den zugehörigen Metriken, 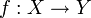 eine Funktion mit Definitionsbereich
eine Funktion mit Definitionsbereich 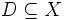 . Folgende Definitionen sind äquivalent:
. Folgende Definitionen sind äquivalent:Epsilon-Delta-Kriterium: f heißt (lokal) stetig in
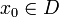 , wenn zu jedem ε > 0 ein δ > 0 existiert, so dass
, wenn zu jedem ε > 0 ein δ > 0 existiert, so dass 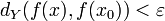 für alle x mit dX(x,x0) < δ gilt.
für alle x mit dX(x,x0) < δ gilt.Folgenkriterium: f ist stetig in x0
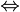 Für jede Folge (xn) aus D, die gegen x0 konvergiert, konvergiert f(xn) gegen f(x0).
Für jede Folge (xn) aus D, die gegen x0 konvergiert, konvergiert f(xn) gegen f(x0).Umgebungskriterium: f ist genau dann stetig in x0, wenn es zu jeder Umgebung V von f(x0) eine Umgebung U von x0 gibt, deren Bild in V enthalten ist, also
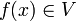 für alle
für alle  .
.In vielen Themen der Analysis kommen stetige Abbildungen zwischen den metrischen Räumen
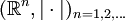 in Betracht. Die Funktion
in Betracht. Die Funktionist zum Beispiel stetig. Hier sind f1(x) = f(x,y0) bei fixiertem y = y0 und f2(x0,y) bei fixiertem x = x0 stetige Funktionen. Dies ist jedoch im Allgemeinen kein ausreichendes Kriterium für die Stetigkeit von f(x,y). Ein Gegenbeispiel könnte man folgendermaßen konstruieren: (r(x,y),φ(x,y)) seien die Polarkoordinaten von (x,y). Dann ist die Funktion
in (0,0) unstetig, obwohl h1(x) = h(x,y) und h2(y) = h(x,y) für jedes y bzw. x stetige Funktionen einer reellen Variable sind. Weitere relevante Klassen stetiger Funktionen bilden die stetigen Funktionen
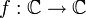 . Die komplexe Exponentialfunktion
. Die komplexe Exponentialfunktion 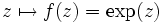 ist Beispiel für eine solche Funktion.
ist Beispiel für eine solche Funktion.Weitere Verallgemeinerung: Stetige Funktionen zwischen topologischen Räumen
Hauptartikel: Stetigkeit (Topologie)
Alle bisherigen Definitionen sind Spezialisierungen der entsprechenden Definition von Stetigkeit in der Topologie. Dort heißt eine Funktion zwischen zwei topologischen Räumen genau dann stetig, wenn die Urbilder offener Mengen wiederum offene Mengen sind. Eine Funktion
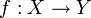 heißt folgenstetig, wenn sie das Folgenkriterium erfüllt, wenn also
heißt folgenstetig, wenn sie das Folgenkriterium erfüllt, wenn alsofür jede konvergente Folge
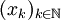 mit Elementen
mit Elementen 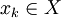 gilt.
gilt.Jede stetige Funktion ist folgenstetig. In Räumen, die das erste Abzählbarkeitsaxiom erfüllen, insbesondere also in metrischen Räumen, gilt auch die Umkehrung, dass jede folgenstetige Funktion stetig ist.[4]
Spezialfälle von Stetigkeit
Spezialfälle der Stetigkeit sind z. B. gleichmäßige Stetigkeit, (lokale) Lipschitz-Stetigkeit sowie absolute Stetigkeit. Die gewöhnliche Stetigkeit wird mitunter auch als punktweise Stetigkeit bezeichnet, um sie gegenüber der gleichmäßigen Stetigkeit abzugrenzen. Anwendungen der Lipschitz-Stetigkeit finden sich z. B. in Eindeutigkeitssätzen (z. B. Satz von Picard-Lindelöf) für Anfangswertprobleme. Die absolute Stetigkeit findet Verwendung in der Stochastik und der Maßtheorie.
Eine Eigenschaft, die eine Menge von Funktionen besitzen kann, ist die gleichgradige Stetigkeit. Sie spielt eine Rolle im häufig verwendeten Satz von Arzelà-Ascoli.
Zusammenhang
Es gelten folgende Zusammenhänge im Fall reeller Funktionen:
f Lipschitz-stetig
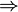 f lokal Lipschitz-stetig
f lokal Lipschitz-stetig 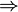 f stetig
f stetigund
f Lipschitz-stetig
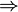 f absolut stetig
f absolut stetig 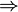 f gleichmäßig stetig
f gleichmäßig stetig 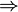 f stetig.
f stetig.Beispiele
Einige Gegenbeispiele sollen demonstrieren, dass die Rückrichtungen in aller Regel nicht gelten:
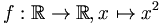 ist lokal Lipschitz-stetig, aber weder Lipschitz-stetig noch gleichmäßig stetig.
ist lokal Lipschitz-stetig, aber weder Lipschitz-stetig noch gleichmäßig stetig.
![f:[-1,1]\rightarrow\mathbb{R}, x\mapsto \sqrt{|x|}](/pictures/dewiki/53/56b61070b1cfd6de881169a2ca89adbe.png) ist stetig, aber nicht lokal Lipschitz-stetig im Nullpunkt.
ist stetig, aber nicht lokal Lipschitz-stetig im Nullpunkt.
Wichtige Sätze über stetige Funktionen
Verkettung stetiger Funktionen
Jede Verkettung stetiger Funktionen ist auch wieder stetig.
Stetigkeit der Umkehrfunktion
Sind I ein Intervall in
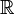 und
und 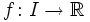 eine stetige, streng monoton wachsende oder streng monoton fallende Funktion, dann ist das Bild von f ein Intervall J,
eine stetige, streng monoton wachsende oder streng monoton fallende Funktion, dann ist das Bild von f ein Intervall J, 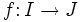 ist bijektiv, und die Umkehrfunktion
ist bijektiv, und die Umkehrfunktion 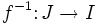 ist stetig. Somit ist f ein Homöomorphismus von I nach J.
ist stetig. Somit ist f ein Homöomorphismus von I nach J.Dies gilt wie angegeben nur für Funktionen, die im gesamten Intervall stetig sind. Ist f eine umkehrbare und an der Stelle x0 stetige Funktion, so ist die Umkehrfunktion f − 1 an der Stelle f(x0) im Allgemeinen nicht stetig. Als Gegenbeispiel sei
![f\colon ]-\infty,0[ \cup [1,+\infty[\rightarrow\mathbb R](/pictures/dewiki/97/a95cb55c89442f5dcb616a0befbec1e9.png) definiert durch:
definiert durch: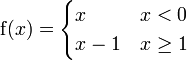 .
.
Dann ist f bijektiv und an der Stelle 1 stetig, aber f − 1 ist in 0 = f(1) unstetig.
Der Zwischenwertsatz
Der Zwischenwertsatz besagt, dass eine auf dem Intervall [a,b] (mit a < b) stetige Funktion jeden Wert zwischen f(a) und f(b) mindestens einmal annimmt.
Formal:
- Ist
![f:[a,b]\to\mathbb{R}](/pictures/dewiki/51/332d0f0f6103ad3c4ec22d3af5b36e7c.png) eine stetige Funktion mit a < b und f(a) < f(b), dann existiert für alle
eine stetige Funktion mit a < b und f(a) < f(b), dann existiert für alle ![d\in[f(a),f(b)]](/pictures/dewiki/101/ea6ead916b1fb174151fd3f093fe9cd0.png) ein
ein ![x\in[a,b]](/pictures/dewiki/56/8290bddba5acf9822dcbf61f4ac67d1b.png) , so dass f(x) = d.
, so dass f(x) = d. - Analog für f(a) > f(b) und
![d\in[f(b),f(a)]](/pictures/dewiki/48/0ddfec0daa3d741cb6cd57058e456500.png) .
.
Eine äquivalente Formulierung ist: Das Bild einer stetigen Funktion auf einem Intervall ist wieder ein Intervall. (Das Bild eines offenen oder halboffenen Intervalles kann aber durchaus ein abgeschlossenes Intervall sein.)
Satz von Bolzano
Als Spezialfall enthält der Zwischenwertsatz folgenden Satz von Bolzano: Nimmt die auf einem abgeschlossenen Intervall stetige Funktion f(x) an zwei Stellen a und b dieses Intervalls Funktionswerte mit unterschiedlichem Vorzeichen an, so gibt es zwischen a und b mindestens eine Stelle c, an der die Funktion f(x) verschwindet (d. h. f(c) = 0 also eine Nullstelle der Funktion).
Satz vom Minimum und Maximum
Eine reellwertige Funktion, die auf einer abgeschlossenen und beschränkten Teilmenge von
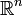 stetig ist, ist beschränkt und nimmt ihre obere und ihre untere Grenze an. Für reelle Funktionen lässt sich das wie folgt umformulieren: Ist
stetig ist, ist beschränkt und nimmt ihre obere und ihre untere Grenze an. Für reelle Funktionen lässt sich das wie folgt umformulieren: Ist ![f\colon[a,b]\to\mathbb{R}](/pictures/dewiki/56/83917025e687324e389eecda76d8f3ec.png) stetig, so gibt es Stellen
stetig, so gibt es Stellen ![t,h\in[a,b]](/pictures/dewiki/51/3cec04b56af7b8a7dadea02a4ee5ba05.png) , so dass
, so dass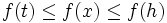 für alle
für alle ![x\in[a,b]](/pictures/dewiki/56/8290bddba5acf9822dcbf61f4ac67d1b.png)
gilt.
Dieser von Weierstraß bewiesene Satz, bisweilen auch Extremwertsatz genannt, liefert nur die Existenz dieser Extremwerte. Für das praktische Auffinden dieser Punkte sind Aussagen aus der Differentialrechnung nützlich.
Diese Aussage gilt auch für stetige reellwertige Funktionen auf beschränkten und abgeschlossenen Teilmengen des
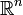 oder auf kompakten topologischen Räumen.
oder auf kompakten topologischen Räumen.Differenzierbarkeit stetiger Funktionen
Stetige Funktionen sind nicht notwendig differenzierbar. Noch Anfang des 19. Jahrhunderts war man überzeugt, dass eine stetige Funktion höchstens an wenigen Stellen nicht differenzierbar sein könne (wie die Betragsfunktion). Bernhard Bolzano konstruierte dann als erster Mathematiker tatsächlich eine Funktion, die überall stetig, aber nirgends differenzierbar ist, was in der Fachwelt allerdings nicht bekannt wurde; Karl Weierstraß fand dann in den 1860er Jahren ebenfalls eine derartige als Weierstraß-Funktion bekannte Funktion, was diesmal unter Mathematikern Wellen schlug. Seine Funktion ist folgendermaßen definiert:
 ,
,
wobei a eine ungerade Zahl ist und
![b \in{]}0,1[](/pictures/dewiki/101/e8e4e7ab444d512fa681c18f684bbede.png) ist mit
ist mit 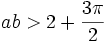 .
.Funktionenräume stetiger Funktionen
Der Raum der stetigen reellwertigen Funktionen auf einem topologischen Raum D ist ein reeller Vektorraum, er wird mit C(D) bezeichnet. In diesem Raum sind insbesondere alle differenzierbaren Funktionen enthalten, falls D eine offene Teilmenge des
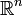 oder einer differenzierbaren Mannigfaltigkeit ist. Funktionen, deren Ableitungen ebenfalls stetig sind, nennt man stetig differenzierbar. Diese Funktionen bilden ebenfalls einen linearen Raum, der C1(D) genannt wird. Entsprechend definiert man Cn(D) als den Raum der Funktionen, die n-mal differenzierbar sind, wobei die n-te Ableitung stetig ist, die also n-mal stetig differenzierbar sind. Des Weiteren bezeichnet
oder einer differenzierbaren Mannigfaltigkeit ist. Funktionen, deren Ableitungen ebenfalls stetig sind, nennt man stetig differenzierbar. Diese Funktionen bilden ebenfalls einen linearen Raum, der C1(D) genannt wird. Entsprechend definiert man Cn(D) als den Raum der Funktionen, die n-mal differenzierbar sind, wobei die n-te Ableitung stetig ist, die also n-mal stetig differenzierbar sind. Des Weiteren bezeichnet  den Raum der beliebig oft differenzierbaren Funktionen.
den Raum der beliebig oft differenzierbaren Funktionen.Einzelnachweise
- ↑ Harro Heuser, Lehrbuch der Analysis. Teil 1. 8. Auflage, B. G. Teubner, Stuttgart 1990. ISBN 3-519-12231-6. Definition 34.6
- ↑ Harro Heuser, Lehrbuch der Analysis. Teil 1. 8. Auflage, B. G. Teubner, Stuttgart 1990. ISBN 3-519-12231-6. S. 212
- ↑ Harro Heuser, Lehrbuch der Analysis. Teil 1. 8. Auflage, B. G. Teubner, Stuttgart 1990. ISBN 3-519-12231-6. Satz 38.2
- ↑ J. Cigler, H.-C. Reichel: Topologie. Eine Grundvorlesung. Bibliographisches Institut, Mannheim 1978, ISBN 3-411-00121-6, S. 43, Aufgabe 61.
Weblinks
Wikimedia Foundation.