- Teilgraphen und Minoren
-
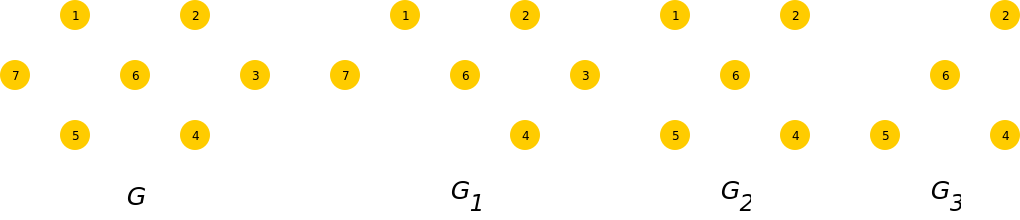
Bei der Untersuchung von Grapheneigenschaften schließt man häufiger von lokalen auf globale Eigenschaften von Graphen und umgekehrt. Um derartige Vorgänge besser beschreiben zu können, definiert man geeignete Relationen zwischen Graphen und lokalen Gebieten innerhalb dieser Graphen. Besonders wichtig sind dabei Teilgraphenbeziehungen. Die Begriffe Teilgraph und Untergraph sind Spezialfälle der entsprechenden allgemeineren Begriffe Teil-Struktur und Unter-Struktur aus der Modelltheorie. Eine Unter-Struktur ist anschaulich gesehen ein Ausschnitt aus einer Struktur, bei der alle Beziehungen zwischen den Elementen (bzw. Knoten) erhalten bleiben. Beispiel siehe unten: G2, G3 sind Untergraphen von G, aber G1 ist kein Untergraph, sondern nur ein Teilgraph von G. In Teil-Strukturen können also zusätzlich noch Beziehungen zwischen den Elementen wegfallen. Jede Unter-Struktur ist eine Teil-Struktur aber nicht umgekehrt. Im folgenden werden beide Begriffe für Graphen näher definiert.
Anschaulich bedeutet es folgendes: Um aus einem Graphen G einen Teilgraph T zu erzeugen wählt man beliebige Knoten aus G und fügt sie T hinzu. Einen Teilgraph erhält man, indem man einige Kanten von T´s Knoten auch zu T hinzufügt. Einen Untergraphen erhält man, indem man alle Kanten zwischen T´s Knoten zu T hinzufügt.
Inhaltsverzeichnis
Definitionen
Teilgraph
Ein Graph G1 = (V1,E1) heißt Teilgraph oder Subgraph von G2 = (V2,E2), falls V1 Teilmenge von V2, also
 und
und- in Graphen ohne Mehrfachkanten E1 Teilmenge von E2 ist,
 ,
, - in ungerichteten Graphen mit Mehrfachkanten
 für alle zweielementigen Teilmengen v von V2, also
, gilt, wobei E1 / 2(v) die Menge der Kanten zwischen den Knoten aus v ist,
für alle zweielementigen Teilmengen v von V2, also
, gilt, wobei E1 / 2(v) die Menge der Kanten zwischen den Knoten aus v ist,
- in gerichteten Graphen mit Mehrfachkanten
 für alle Teilmengen v aus dem kartesischen Produkt V2xV2 gilt.
für alle Teilmengen v aus dem kartesischen Produkt V2xV2 gilt.
Umgekehrt heißt G2 Supergraph oder Obergraph von G1.
Bei einem knotengewichteten bzw. kantengewichteten Graph G2 wird von einem Teilgraph G1 zudem verlangt, dass die Gewichtsfunktion g1 von G1 kompatibel zu der Gewichtsfunktion g2 von G2 ist, d.h. für jeden Knoten v bzw. für jede Kante e von G2 gilt g1(v) = g2(v) bzw. g1(e) = g2(e).
Untergraph bzw. Induzierter Teilgraph
Gilt zusätzlich:
- in Graphen ohne Mehrfachkanten,
, d.h. G1 enthält alle Kanten zwischen den Knoten in V1, die auch in G2 vorhanden sind.

- in ungerichteten Graphen mit Mehrfachkanten,
für alle zweielementigen Teilmengen v von V2,

- in gerichteten Graphen mit Mehrfachkanten,
für alle v aus dem kartesischen Produkt V2xV2,

so bezeichnet man G1 auch als den durch V1 induzierten Teilgraph von G2 und notiert diesen auch mit G2[V1] oder auch einfach GA (G=G2, A=V1).
Bemerkungen:
- Induzierte Teilgraphen sind immer eindeutig durch die entsprechende Knotenmenge festgelegt.
- Besonders wichtige Teilgraphen entstehen durch das Weglassen von Knoten bzw. Kanten. Sei der Graph G(V,E) gegeben, dann bezeichnet
den Graphen, der durch Weglassen der Knoten aus A und aller mit diesen Knoten inzidenten Kanten entsteht. Die so entstehenden Teilgraphen sind immer induzierte Teilgraphen.

Beispiele
In der folgenden Abbildung sind die Graphen G1, G2, G3 Teilgraphen von G, wobei aber nur G2 und G3 induzierte Teilgraphen sind. G3 entsteht dabei aus G durch Weglassen der Knoten 1,3,7 und ihrer inzidenten Kanten.
Minor
Ein Graph G1 wird Minor des Graphen G2 genannt, falls G1 isomorph aus einem Teilgraphen von G2 durch Kantenkontraktion entsteht. Mit anderen Worten: G1 muss aus G2 durch Löschen von Knoten und/oder Kanten und/oder Kantenkontraktion gewonnen werden können. Kantenkontraktion bedeutet, dass zwei adjazente (benachbarte) Knoten V1 und V2 unter Entfernung einer zu diesen beiden Knoten inzidenten Kante zu einem Knoten V12 verschmolzen werden. Dieser Knoten V12 hat zu allen Knoten Kanten, zu denen zuvor V1 oder V2 eine Kante hatte.
Zum Beispiel ist in der folgenden Abbildung G1 ein Minor von G2.

Die Minor-Beziehung definiert eine partielle Ordnungsrelation auf den Isomorphie-Klassen von Graphen.
Neil Robertson und Paul Seymour (Satz von Robertson und Seymour) haben gezeigt, dass für jede unendliche Folge G1, G2,... von endlichen Graphen stets Indizes i und j mit i < j existieren, so dass Gi ein Minor von Gj ist.
Siehe auch
Literatur
- Lutz Volkmann: Fundamente der Graphentheorie, Springer (Wien) 1996, ISBN 3-211-82774-9 (neuere, elektronische Online-Version "Graphen an allen Ecken und Kanten")
- Reinhard Diestel: Graphentheorie. Springer 2006, ISBN 3-540-21391-0 (elektronische Online-Version)
Weblinks
- Eric W. Weisstein: Graph Minor. In: MathWorld. (englisch)
- Eric W. Weisstein: Subgraph. In: MathWorld. (englisch)
- Minor eines Graphen in der Encyclopaedia of Mathematics
- in Graphen ohne Mehrfachkanten E1 Teilmenge von E2 ist,
Wikimedia Foundation.