- Banach-Algebra
-
Banach-Algebra berührt die Spezialgebiete
ist Spezialfall von
- Abelsche Gruppe
- Ring
- Vektorraum
- Algebra
- Topologische Algebra
- Algebra
- topologischer Raum
umfasst als Spezialfälle
Banachalgebren (nach Stefan Banach) sind mathematische Objekte der Funktionalanalysis, die einige bekannte Funktionenräume anhand wesentlicher gemeinsamer Eigenschaften verallgemeinern (z. B. Mengen stetiger oder integrierbarer Funktionen).
Eine Banachalgebra ist ein Vektorraum, in dem zusätzlich auch eine Multiplikation und eine Norm so definiert sind, dass gewisse Verträglichkeitsbedingungen erfüllt sind.
Inhaltsverzeichnis
Definition
Ein Vektorraum (V,+)
- über dem Körper
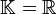 oder
oder 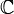
- mit einer Norm
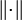
- und einem Produkt
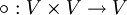
ist eine Banachalgebra, wenn gilt:
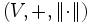 ist ein Banachraum, also ein vollständiger normierter Vektorraum,
ist ein Banachraum, also ein vollständiger normierter Vektorraum,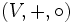 ist eine assoziative
ist eine assoziative 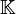 -Algebra,
-Algebra,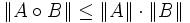 , d. h. die Norm ist submultiplikativ.
, d. h. die Norm ist submultiplikativ.
Wie auch in der Algebra allgemein üblich wird das Symbol für das Produkt gern weggelassen. Nur im Falle der Faltung wird oft das Symbol * oder
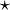 verwendet.
verwendet.Banach-*-Algebra oder involutive Banachalgebra
Definition: Eine Banach-*-Algebra
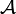 (über
(über 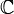 ) ist eine Banachalgebra zusammen mit einer *-Involution
) ist eine Banachalgebra zusammen mit einer *-Involution 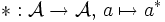 , so dass
, so dass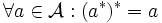 (involutiv)
(involutiv)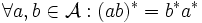 (anti-multiplikativ)
(anti-multiplikativ)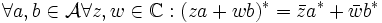 (semilinear, anti-linear oder konjugiert linear)
(semilinear, anti-linear oder konjugiert linear)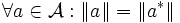 (isometrisch)
(isometrisch)
C*-Algebra
Die Banachalgebra B(H) (H ein Hilbertraum) motiviert die folgende Definition: Eine Banachalgebra V, auf der zusätzlich eine semilineare Involution
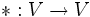 gegeben ist, heißt C*-Algebra, wenn gilt:
gegeben ist, heißt C*-Algebra, wenn gilt: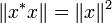 für alle
für alle 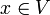
Von-Neumann-Algebren sind spezielle C*-Algebren.
Beispiele
- Jeder Banachraum wird mit der Null-Multiplikation, d.h. xy=0 für alle Elemente x,y des Banachraums, zu einer Banachalgebra.
- Sei K ein kompakter Raum und
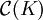 der Raum der stetigen Funktionen
der Raum der stetigen Funktionen 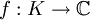 . Mit den punktweise Operationen und der durch
. Mit den punktweise Operationen und der durch 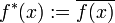 (komplexe Konjugation) definierten Involution und der Supremumsnorm
(komplexe Konjugation) definierten Involution und der Supremumsnorm 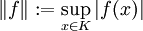 wird
wird 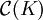 zu einer kommutativen C*-Algebra.
zu einer kommutativen C*-Algebra.
- Sei D der Einheitkreis in
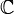 . Es sei A(D) die Algebra mit stetigen Funktionen
. Es sei A(D) die Algebra mit stetigen Funktionen 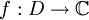 , die im Inneren von D holomorph sind. Mit den punktweise Operationen und der durch
, die im Inneren von D holomorph sind. Mit den punktweise Operationen und der durch 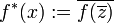 (komplexe Konjugation) definierten Involution und der Supremumsnorm wird A(D) zu einer kommutativen Banach-*-Algebra, die keine C*-Algebra ist.
(komplexe Konjugation) definierten Involution und der Supremumsnorm wird A(D) zu einer kommutativen Banach-*-Algebra, die keine C*-Algebra ist.
- Ist V ein Banachraum, so ist die Algebra B(V) der stetigen, linearen Operatoren auf V eine Banachalgebra, die im Falle dim(v) > 1 nicht kommutativ ist. Ist V ein Hilbertraum, so ist B(V) eine C*-Algebra.
- Die Spurklasse und die Hilbert-Schmidt-Klasse, oder allgemeiner die Schatten-Klassen, sind Beispiele für nicht-kommutative Banach-*-Algebren, die keine C*-Algebren sind.
- In der harmonischen Analyse werden die Banach-*-Algebren L1(G), d.h. die Faltungsalgebren über einer lokalkompakten Gruppe G betrachtet.
Grundlagen
Es werden einige Grundlagen der Theorie der Banachalgebren besprochen, die ein Zusammenspiel zwischen algebraischen und topologischen Eigenschaften zeigen.
Das Einselement
Viele der oben genannten Beispiele sind Banachalgebren ohne ein Einselement. Wird dennoch ein Einselement benötigt, so kann man eines adjungieren. In vielen Fällen gibt es in diesen Banachalgebren Approximationen der Eins; dies ist ein topologisches Konstrukt, das oft einen Ersatz für das fehlende Einselement darstellt. Das gilt insbesondere für C*-Algebren und die Gruppenalgebren L1(G).
Die Gruppe der invertierbaren Elemente
Ist A eine Banachalgebra mit Einselement 1, so ist die Gruppe A − 1 der invertierbaren Elemente offen. Ist nämlich
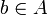 invertierbar und
invertierbar und 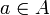 mit
mit 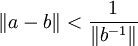 , so ist auch a invertierbar, denn leicht überlegt man sich, dass
, so ist auch a invertierbar, denn leicht überlegt man sich, dass 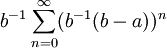 konvergiert und das Inverse zu a ist. Ferner ist das Invertieren
konvergiert und das Inverse zu a ist. Ferner ist das Invertieren 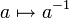 als Abbildung auf der Gruppe der invertierbaren Elemente stetig. Daher ist A − 1 eine topologische Gruppe.
als Abbildung auf der Gruppe der invertierbaren Elemente stetig. Daher ist A − 1 eine topologische Gruppe.Das Spektrum
In der linearen Algebra spielt die Menge der Eigenwerte einer Matrix eine wichtige Rolle bei der Untersuchung der Matrizen, d.h. der Elemente der Banachalgebra
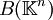 . Dies verallgemeinert sich zum Begriff des Spektrums:
. Dies verallgemeinert sich zum Begriff des Spektrums:Sei A eine
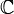 -Banachalgebra mit Einselement. Für
-Banachalgebra mit Einselement. Für 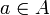 ist das Spektrum von a,
ist das Spektrum von a, 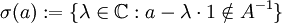 , kompakt und nach dem Satz von Gelfand-Mazur nicht leer. Für den Spektralradius
, kompakt und nach dem Satz von Gelfand-Mazur nicht leer. Für den Spektralradius 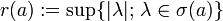 gilt die Formel
gilt die Formel 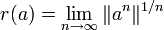 . Diese Formel ist insofern erstaunlich, als dass der Spektralradius eine rein algebraische Größe ist, die lediglich den Begriff der Invertierbarkeit verwendet. Die rechte Seite der Spektralradiusformel hingegen ist durch die Norm der Banachalgebra gegeben.
. Diese Formel ist insofern erstaunlich, als dass der Spektralradius eine rein algebraische Größe ist, die lediglich den Begriff der Invertierbarkeit verwendet. Die rechte Seite der Spektralradiusformel hingegen ist durch die Norm der Banachalgebra gegeben.Die Menge XA aller multiplikativen Funktionale
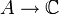 bezeichnet man als das Spektrum (Gelfand-Spektrum) oder als den Gelfand-Raum von A. Das Spektrum von A ist ein kompakter Raum und die Gelfand-Transformation vermittelt einen Homomorphismus
bezeichnet man als das Spektrum (Gelfand-Spektrum) oder als den Gelfand-Raum von A. Das Spektrum von A ist ein kompakter Raum und die Gelfand-Transformation vermittelt einen Homomorphismus 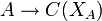 von A in die Banachalgebra der stetigen komplexwertigen Funktionen auf XA. Jedem Element
von A in die Banachalgebra der stetigen komplexwertigen Funktionen auf XA. Jedem Element 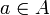 wird so eine stetige Funktion
wird so eine stetige Funktion 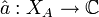 zugeordnet, wobei
zugeordnet, wobei  . Das Spektrum eines Elementes
. Das Spektrum eines Elementes 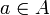 und das Spektrum der Algebra hängen dann über die Formel
und das Spektrum der Algebra hängen dann über die Formel 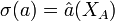 zusammen. Das ist im Artikel über die Gelfand-Transformation ausgeführt.
zusammen. Das ist im Artikel über die Gelfand-Transformation ausgeführt.Maximale Ideale
Sei A eine kommutative
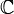 -Banachalgebra mit Einselement. Ist
-Banachalgebra mit Einselement. Ist 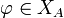 , so ist
, so ist 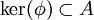 ein maximales Ideal (mit Kodimension 1). Ist umgekehrt
ein maximales Ideal (mit Kodimension 1). Ist umgekehrt 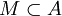 ein maximales Ideal, so ist der Abschluss
ein maximales Ideal, so ist der Abschluss 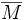 wegen der Offenheit der Gruppe der invertierbaren Elemente ein echtes Ideal, also muss
wegen der Offenheit der Gruppe der invertierbaren Elemente ein echtes Ideal, also muss 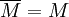 gelten. Dann ist die Quotientenalgebra A / M eine Banachalgebra, die ein Körper ist, und dieser muss nach dem Satz von Gelfand-Mazur isomorph zu
gelten. Dann ist die Quotientenalgebra A / M eine Banachalgebra, die ein Körper ist, und dieser muss nach dem Satz von Gelfand-Mazur isomorph zu 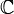 sein. Daher ist die Quotientenabbildung
sein. Daher ist die Quotientenabbildung 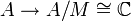 ein multiplikatives Funktional mit Kern M. Bezeichnet man also die Menge der maximalen Ideale mit Max(A), so hat man eine bijektive Abbildung:
ein multiplikatives Funktional mit Kern M. Bezeichnet man also die Menge der maximalen Ideale mit Max(A), so hat man eine bijektive Abbildung: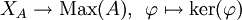
Es besteht damit eine bijektive Beziehung zwischen der Teilmenge XA des Dualraums und der rein algebraisch definierten Menge der maximalen Ideale.
Anwendungen
- Anwendung finden Banachalgebren u. a. in der Operatorentheorie, wie sie z. B. in der Quantenfeldtheorie benutzt wird.
- Ferner gibt es die Erweiterung zu von-Neumann-Algebren und Hilbert-Moduln und der abstrakten K- und KK-Theorie, welche auch als nichtkommutative Geometrie bezeichnet wird.
- Zur Untersuchung lokalkompakter Gruppen zieht man in der harmonischen Analyse die Banachalgebren L1(G) heran.
Literatur
- R.V. Kadison, J. R. Ringrose, Fundamentals of the Theory of Operator Algebras I + II, 1983
- M. Takesaki, Theory of Operator Algebras I (Springer 1979, 2002)
- Abelsche Gruppe
Wikimedia Foundation.
