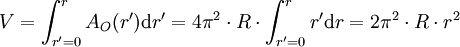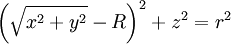- Toroid
-
Ein Torus (lat. torus: "Wulst", Plural: Tori) ist ein geometrisches Gebilde, das wulstartig aufgebaut ist und mit der Form eines Schwimmreifens oder Donuts verglichen werden kann. Genauer wird in drei Formen unterschieden:
- Eingebettete Tori
- Sie entsprechen der Oberfläche eines Volltorus (s. u.) (beispielsweise eines Reifens oder Schmalzkringels) als Teilmenge des dreidimensionalen Raumes.
- Flache Tori
- Sie unterscheiden sich aus topologischer Sicht nicht von eingebetteten Tori, sind jedoch nicht gekrümmt und lassen sich deshalb auch nicht als Teilmenge des dreidimensionalen Raumes beschreiben, sondern als Quotientenraum der Ebene oder als kartesisches Produkt zweier Kreise.
- Volltori
- Sie entsprechen einem gefüllten eingebetten Torus (s. o.) (beispielsweise einem gefüllten Reifen) als Teilmenge des dreidimensionalen Raumes. Sie sind also geometrische Körper.
Daneben gibt es noch Tori in der Theorie der Liegruppen, siehe Torus (Liegruppe), und algebraischen Gruppen, siehe Algebraischer Torus.
Inhaltsverzeichnis
Eingebettete Tori
Ein eingebetteter Torus kann als Menge der Punkte beschrieben werden, die von einem Kreis mit Radius R den Abstand r < R haben.
Toruskoordinaten
Man kann in der Torusoberfläche, die topologisch eine Fläche von Geschlecht 1 ist (d. h. sie besitzt ein Loch), eine toroidale Koordinate t und eine dazu senkrechte poloidale Koordinate p einführen. Man kann sich die Oberfläche durch einen Kreis entstanden vorstellen, der um eine Achse, die in der Kreisebene liegt, rotiert wird. Den Radius des ursprünglichen Kreises nennen wir r, dieser Kreis bildet auch gleichzeitig eine Koordinatenlinie von p. Der Abstand des Kreismittelpunkts von der Achse wird hier R genannt, die Koordinatenlinien von t sind Kreise um die Drehachse. Beide Koordinaten sind Winkel und laufen von 0 bis 2π.

Eine mögliche Umrechnung in kartesische (dreidimensionale) Koordinaten ist (
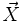 ist hier der Ortsvektor)
ist hier der Ortsvektor)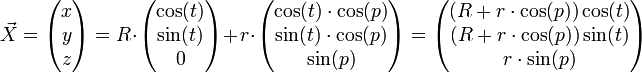
Man gewinnt diese Darstellung z.B. aus den Parametrisierungen des Ortsvektors in der x-y-Ebene und x-z-Ebene.
Volumen und Oberfläche
Da der Torus ein Rotationskörper ist, kann man Volumen und Oberfläche mittels der guldinschen Regel berechnen. Ganz simpel gesehen ist ein Torus ein vollständig gekrümmter Kreiszylinder dessen Mantelfläche und Volumen sich während des „knickfreien Biegens“ erstaunlicherweise nicht verändern. Denn die Innenseite wird dabei um den gleichen Faktor linear gestaucht um welchen die Außenseite gedehnt wird – entsprechend den Abständen der rechteckigen Zylinderquerschnitte zum großen Zylinderquerschnitt, der durch die Schwerpunkte der Zylinderkreise verläuft und parallel zur Torusachse ist (siehe: Prinzip von Cavalieri).
Die nach außen zeigende Flächennormale ist in kartesischen Koordinaten
Das Flächenelement ist
Durch Integration erhält man die Oberfläche des Torus:
Eine Teilfläche des Torus erhält man durch Integration in den Grenzen t1 bis t2 (horizontal) und p1 bis p2 (vertikal):
ergibt
Zur Berechnung des Volumens des Volltorus setzt man statt r die Variable r' ein und lässt sie von 0 (zu Kreis entarteter Torus, kein Volumen) bis r variieren:
Das Torusvolumen ist das Integral der Oberfläche (über r).
Algebraische Gleichung
Der Rotationstorus lässt sich auch durch die folgende Gleichung in den Koordinaten x,y,z beschreiben:
- (R2 − r2)2 + 2R2(z2 − x2 − y2) − 2r2(x2 + y2 + z2) + (x2 + y2 + z2)2 = 0
oder
- (x2 + y2 + z2 + R2 − r2)2 − 4R2(x2 + y2) = 0.
Sie lässt sich beispielsweise aus der Gleichung
herleiten, die sich aus dem Satz des Pythagoras ergibt.
Typen von Tori
Dabei hat nur der zweite Torus das Geschlecht 1, die anderen beiden, da sie kein Loch haben, das Geschlecht 0.
Flache Tori
Ein flacher Torus kann beschrieben werden durch ein Parallelogramm, dessen gegenüberliegende Seiten zusammengeklebt werden. Äquivalent dazu können flache Tori als topologische Faktorgruppen
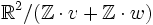 für zwei linear unabhängige Vektoren
für zwei linear unabhängige Vektoren 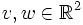 beschrieben werden. Im Spezialfall v = (1,0) und w = (0,1) erhält man den Quotienten
beschrieben werden. Im Spezialfall v = (1,0) und w = (0,1) erhält man den Quotienten 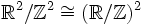 .
.Diese Tori heißen flach, weil ihre Metrik lokal der Metrik der Ebene entspricht und ihre Krümmung deshalb verschwindet.
Elliptische Kurven über den komplexen Zahlen sind (mit einer translationsinvarianten Metrik) Beispiele für flache Tori.
Torustopologie
Im Gegensatz zur Oberfläche einer Kugel kann der Torus ohne Singularitäten auf einer ebenen, rechteckigen Fläche abgebildet werden.
Dabei wird die rechte Kante des Rechtecks oder Quadrates mit seiner linken Kante verheftet, und seine untere Kante wird mit seiner oberen Kante verheftet. Diese Topologie besitzen auch viele Computerspiele, zum Beispiel Pacman oder das Game of Life.
Volltori
Eingebettete Volltori lassen sich wie eingebettete Tori beschreiben, in der oben angegebenen Parameterdarstellung ist lediglich r durch einen Parameter ρ mit Wertebereich
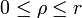 zu ersetzen. Topologisch ist ein Volltorus homöomorph zum kartesischen Produkt
zu ersetzen. Topologisch ist ein Volltorus homöomorph zum kartesischen Produkt 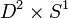 der Kreisscheibe mit der Kreislinie.
der Kreisscheibe mit der Kreislinie.Die 3-Sphäre, also der dreidimensionale Raum zusammen mit einem unendlich fernen Punkt, lässt sich als Vereinigung zweier Volltori, die sich lediglich in ihrer Oberfläche überlappen, darstellen. Man erhält sie beispielsweise aus der Hopf-Faserung, indem man den Basisraum S2 als Vereinigung von Nord- und Südhalbkugel auffasst; über beiden Hälften ist die Faserung trivial. Die Zerlegung der 3-Sphäre in zwei Volltori wird beispielsweise bei der Konstruktion der Reeb-Blätterung ausgenutzt.
Höherdimensionale Tori
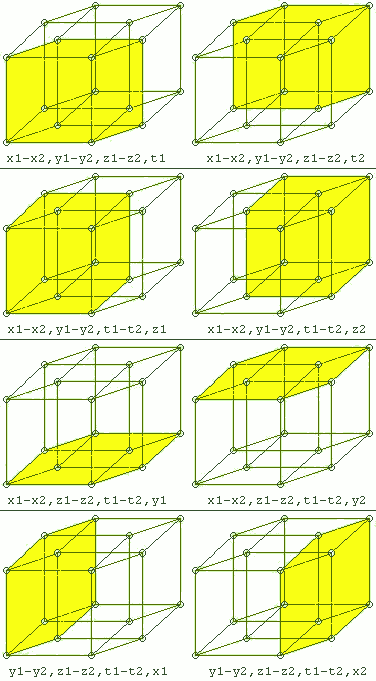
Beim 3-dimensionalen Torus oder 3-Torus handelt es sich um einen Quader oder Würfel, dessen sechs gegenüberliegende Flächen paarweise miteinander verheftet sind.
Beim 4-dimensionalen Torus oder 4-Torus handelt es sich um einen Tesserakt, dessen acht gegenüber liegende Würfel paarweise miteinander verheftet sind.
Allgemein ist der n-dimensionale Torus ein n-dimensionaler Würfel [0,1]n, dessen gegenüberliegende (n-1)-Hyperwürfel paarweise miteinander identifiziert sind. Man kann ihn auch als
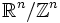 darstellen.
darstellen.Das (n+1) - dimensionale „Volumen“ eines n-Torus ist
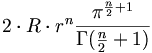 ,
,die n - dimensionale „Oberfläche“
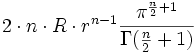 .
.Weblinks
Wikimedia Foundation.


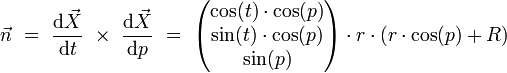
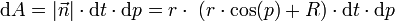
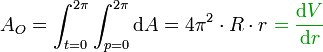
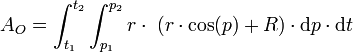
![A_O = (t_2 - t_1) \cdot [r^2 \cdot(\sin(p_2) - \sin(p_1)) + r \cdot R \cdot (p_2 - p_1)]](/pictures/dewiki/102/fb81089c2f0c10d1850c55e423245f57.png)