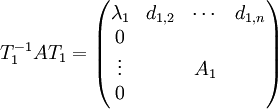Trigonalisierbar

Die Trigonalisierung ist ein Begriff aus der linearen Algebra, einem Teilgebiet der Mathematik. Sie bezeichnet eine Ähnlichkeitsabbildung einer quadratischen Matrix auf eine obere Dreiecksmatrix. Dies ist nicht für jede quadratische Matrix möglich und man bezeichnet deshalb Matrizen die zu einer oberen Dreiecksmatrix ähnlich sind als trigonalisierbare Matrizen. Entsprechend bezeichnet man einen Vektorraum-Endomorphismus als trigonalisierbaren Endomorphismus, wenn es unter seinen Darstellungsmatrizen eine obere Dreieckmatrix gibt.

Zwischen trigonalisierbaren Matrizen und trigonalisierbaren Endomorphismen gibt es einen Zusammenhang: die trigonalisierbaren Matrizen sind die Darstellungsmatrizen der trigonalisierbaren Endomorphismen.

Kriterien für die Trigonalisierbarkeit

Folgende Aussagen sind äquivalent und legen damit fest, ob eine Matrix trigonalisierbar ist:

• die Matrix A ist über dem Körper K trigonalisierbar.
• die Matrix A ist ähnlich zu einer oberen Dreiecksmatrix. Das heißt es existiert eine obere Dreiecksmatrix D und eine invertierbare Matrix P mit D = P ^{− 1}AP.
• das charakteristische Polynom der Matrix A zerfällt über dem Körper K in Linearfaktoren.
• das Minimalpolynom der Matrix A zerfällt über dem Körper K in Linearfaktoren.
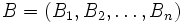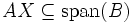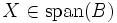• es gibt eine Basis $B = (B_1, B_2, \dots, B_n)$, sodass $AX \subseteq {\rm span}(B)$ mit $X \in {\rm span}(B)$. Die Basis B nennt man eine Fahnenbasis.

Berechnung der oberen Dreiecksmatrix

Um die gesuchte obere Dreiecksmatrix D zu berechnen, berechnen wir zuerst die Matrix P mit der die Ähnlichkeitsabbildung durchgeführt wird. Es gilt:

D = P ^{− 1}AP

Des Weiteren haben A und D dieselben Eigenwerte.

Da das charakteristische Polynom von A in Linearfaktoren zerfällt, gibt es einen Eigenwert λ₁ und einen zugehörigen Eigenvektor v₁. Dieser Eigenvektor wird nun zu einer Basis 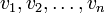$v_1, v_2, \dots, v_n$ des Kⁿ ergänzt. Die Matrix T₁ sei die Basiswechselmatrix zum Basiswechsel von der Einheitsbasis nach 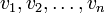$v_1, v_2, \dots, v_n$. Damit lässt sich 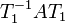$T_1^{-1}AT_1$ berechnen und die Form

$T_1^{-1}AT_1 = \begin{pmatrix} \lambda_1 & d_{1,2} & \cdots & d_{1,n} \\ 0 & & & \\ \vdots & & A_1 & \\ 0 & & & \end{pmatrix}$

Für das charakteristische Polynom der 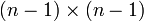$(n-1)\times(n-1)$-Matrix A₁ gilt 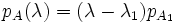$p_A(\lambda) = (\lambda - \lambda_1)p_{A_1}$. Es zerfällt daher auch in Linearfaktoren und A₁ ist somit selbst wieder trigonalisierbar. Dieses Verfahren lässt sich nun fortsetzen, bis man A_{n − 1} = d_n,n berechnet hat. Die dabei entstehende Matrix ist genau die Dreiecksmatrix D. Die Matrix P ergibt sich als Produkt $T_1 T_2 \dots T_{n-1}$ der Basiswechselmatrizen.

Siehe auch

• Schurzerlegung ist ein Beispiel für ein Trigonalisierungsverfahren über 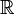$\mathbb{R}$ oder $\mathbb{C}$

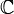
Literatur

Gerd Fischer: Lineare Algebra, ISBN 3-528-03217-0