- Trouton-Noble-Experiment
-
Mit dem Trouton-Noble-Experiment versuchten Frederick Thomas Trouton und Henry R. Noble 1903 auf eine andere Art als beim Michelson-Morley-Experiment den Bewegungszustand der Erde relativ zum Äther zu messen. Der negative Ausgang des Trouton-Noble-Versuchs war neben dem Michelson-Morley-Versuch eine der wichtigsten frühen Bestätigungen der speziellen Relativitätstheorie, und wurde mehrmals mit demselben Resultat wiederholt (vgl. Tests der speziellen Relativitätstheorie).
Damit zusammenhängend existieren auch eine Reihe von Paradoxien der relativistischen Statik, die beispielsweise als „Trouton-Noble-Paradoxon“ oder „Winkelhebelparadoxon“ bekannt sind. Hier geht es darum, ob durch den Wechsel des Inertialsystems ein Drehmoment bzw. eine Rotation in einem statischem Systems eintritt. Es wurden dazu eine Reihe von Lösungen vorgeschlagen, die darin übereinstimmen, dass keine Rotation auftritt.
Inhaltsverzeichnis
Trouton-Noble-Experiment
Bei diesem Versuch wurde ein geladener Plattenkondensator benutzt. Dieser ist so konstruiert, dass er sich frei um eine zu den Platten parallele Achse drehen kann, so er einem Drehmoment unterworfen wäre. Wenn nun die Erde und der Kondensator eine Geschwindigkeit v haben, repräsentiert jede geladene Kondensatorplatte einen Strom, dessen Magnetfeld B auf die andere Platte eine Lorentz-Kraft F und damit ein Drehmoment ausüben sollte. Bei einer „Ätherwindgeschwindigkeit“ v in einem Winkel zur senkrechten Verbindungslinie der beiden Platten ergäbe sich das (letztlich vom Winkel unabhängige) Drehmoment zu
(E: Feldenergie im Kondensator; c: Lichtgeschwindigkeit). Bei dem Versuch konnten jedoch keinerlei Drehmomente nachgewiesen werden. Es stellte somit (zusammen mit dem Michelson-Morley-Experiment) einen bedeutenden Einwand gegen die Auffassung eines ruhenden Äthers bzw. eines bevorzugten Bezugssystems dar.[1] [2] Ähnliche Experimente wurden später auch mit noch größerer Präzision aber demselben negativen Resultat, von Rudolf Tomaschek (1925, 1926), Carl T. Chase (1926, 1927) und Howard C. Hayden (1994) wiederholt.[3] [4] [5] [6] [7] [8]
Dieses Ergebnis stimmt mit der aus der speziellen Relativitätstheorie folgenden Erwartung überein, dass die Experimentalanordnung gemäß dem Relativitätsprinzip als in einem Inertialsystem ruhend betrachtet werden kann, und folglich auch kein positives Ergebnis auftreten kann.
Dies muss auch für alle anderen Inertialsysteme gelten, da eine Lorentz-Transformation (welche die Koordinaten der Inertialsysteme miteinander verbindet) das Ergebnis nicht verändert. Jedoch erwies sich deren Anwendung auf statische und dynamische Probleme als recht schwierig, und es wurden unterschiedliche Modelle vorgeschlagen um das „Trouton-Noble-Paradoxon“ (ob nämlich ein Drehmoment in relativ bewegten Inertialsystem auftritt oder nicht) zu lösen.
Winkelhebelparadoxon
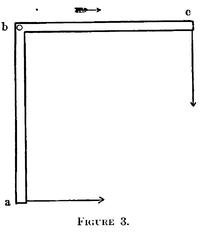
Das Trouton-Noble-Paradoxon ist im Wesentlichen äquivalent mit dem sogenannten „Winkelhebelparadoxon“ (Right-angle lever paradox), das erstmals von Gilbert Newton Lewis und Richard C. Tolman (1909) behandelt wurde.[9] Es sei ein Winkelhebel mit Endpunktion abc gegeben. In seinem Ruhesystem sind die Kräfte fy' in Richtung ba und fx' in Richtung bc gleich groß sodass Gleichgewicht herrscht, deshalb existiert kein Drehmoment gemäß dem Hebelgesetz:
wo L0 die Länge eines Hebelarms ist. Wird dies hingegen aus eine relativ dazu bewegten System betrachtet, so ist ba länger als bc aufgrund der Längenkontraktion. Das Hebelgesetz ergibt in diesem Fall:
Das Drehmoment ist also nicht null, was den Hebel scheinbar in Rotation versetzen müsste. Da dies aber nicht der Fall sein kann, schlossen Lewis und Tolman, dass kein Drehmoment vorliegt. Folglich setzten sie:
Jedoch zeigte Max von Laue (1911)[10], dass dies im Widerspruch steht mit dem relativistischen Ausdruck der Kraft:
woraus sich ergibt
Angewendet auf das Hebelgesetz, ergibt sich folgendes Drehmoment:
was prinzipiell dasselbe Problem ist wie beim Trouton-Noble-Paradoxon.
Lösungen
Die detaillierte relativistische Analyse dieser Paradoxien erfordert eine sorgfältige Berücksichtigung der relevanten Kräfte und Impulse. Dafür wurden verschiedenen Ansätze vorgelegt, die allesamt darin übereinstimmen, dass keine Rotation eintritt.
Laue-Strom
Die erste Lösung des Trouton-Noble-Paradoxons wurde durch Hendrik Antoon Lorentz (1904) gegeben. Sie beruht auf der Annahme, dass Impuls und Drehmoment der elektrostatischen Kräfte kompensiert werden durch Impuls und Drehmoment der molekularen Bindungskräfte.[11]
Dies wurde von Max von Laue (1911) fortgeführt, der die Standardlösung für dieses Paradoxon gab. Sie basierte auf der „Trägheit der Energie“, wonach durch elastische Spannungen ein Energiefluss erzeugt wird, der ebenfalls mit einem Impuls ausgestattet ist ("Laue-Strom"). Das resultierende (mechanische) Drehmoment im Falle des Trouton-Noble-Experiments ist
und im Falle des Winkelhebels:
was das oben erwähnte elektromagnetische Drehmoment exakt kompensiert, sodass keine Rotation entsteht. Oder mit anderen Worten: Das elektromagnetische Drehmoment ist sogar notwendig um die gleichförmige Bewegung eines gespannten Körpers zu ermöglichen, d.h. um den Körper daran zu hindern, aufgrund des mechanischen Drehmoments zu rotieren.[12] [10] [13] [14]
Seitdem wurden eine Reihe von Arbeiten veröffentlicht, die Laues Lösung weiterentwickelten bzw. modifizierten. Andere Autoren wiederum kritisierten das Konzept des Laue-Stroms, und versuchten das Auftreten eines Drehmoments von vornherein zu vermeiden, und zwar durch Neudefinitionen der Konzepte von Kraft, Gleichgewicht usw. (siehe die Liste der weiterführenden Literatur).
Kraft und Beschleunigung
Eine einfache Lösung, die ohne Kompensationskräfte und ohne Neudefinitionen auskam, wurde von Paul Sophus Epstein (1911) gegeben.[15][16] Er verwies darauf, dass Kraft und Beschleunigung in der Relativitätstheorie nicht notwendigerweise in dieselbe Richtung weisen, d.h. der Zusammenhang von Masse, Kraft und Beschleunigung hat Tensorcharakter. Die von der Kraft gespielten Rolle in der Relativitätstheorie ist also sehr unterschiedlich zur klassischen Mechanik.
Ein Beispiel: Es sei ein masseloser Stab mit Endpunkten OM gegeben. Dieser ist am Punkt O befestigt, wobei ein Körper mit der Masse m bei M befestigt ist. Der gesamte Stab schließt den Winkel
 mit O ein. Nun wirkt bei M eine Kraft in Richtung OM, wobei Gleichgewicht im Ruhesystem dann herrscht, wenn
mit O ein. Nun wirkt bei M eine Kraft in Richtung OM, wobei Gleichgewicht im Ruhesystem dann herrscht, wenn  . Wie bereits oben erwähnt, ist die Form dieser Kräfte in einem relativ dazu bewegten System:
. Wie bereits oben erwähnt, ist die Form dieser Kräfte in einem relativ dazu bewegten System:Also
 .
.Die resultierende Kraft zeigt also nicht direkt von O zu M. Wie Epstein zeigte, führt dies jedoch nicht zu einer Rotation, denn nun betrachtete er die von den Kräften verursachten Beschleunigungen. Die relativistischen Ausdrücke für den Zusammenhang von Masse, Beschleunigung und Kraft sind in longitudinaler und transversaler Richtung:
 , wo
, wo  .
.
Also
 .
.Folglich tritt auch in diesem System keine Rotation auf. Ähnliche Überlegungen gelten auch für das Trouton-Noble- und das Winkelhebelparadoxon. Die Paradoxien sind damit also aufgelöst, weil die beiden Beschleunigungen (als Vektoren) zum Schwerpunkt des Systems (Kondensator bei Trouton-Noble) zeigen, obwohl die Kräfte dies nicht tun.
Epstein fügte hinzu, dass wenn man es befriedigender findet, auch in der Relativitätstheorie die Proportionalität zwischen Kraft und Beschleunigung wiederherzustellen (wie in der gewohnten Newtonschen Mechanik), dann müssen Kompensationskräfte eingeführt werden, welche formal mit Laues Strom übereinstimmen. Epstein entwickelte einen solchen Formalismus in den folgenden Abschnitten seiner 1911er-Arbeit.
Siehe auch
Einzelnachweise
- ↑ F. T. Trouton, H. R. Noble: The mechanical forces acting on a charged electric condenser moving through space. In: Phil. Trans. Royal Soc. A. 202, 1903, S. 165–181.
- ↑ F. T. Trouton, H. R. Noble: The Forces Acting on a Charged Condenser moving through Space. In: Proc. Royal Soc. 74, Nr. 479, 1903, S. 132-–133.
- ↑ R. Tomaschek: Über Versuche zur Auffindung elektrodynamischer Wirkungen der Erdbewegung in großen Höhen I. In: Annalen der Physik. 78, 1925, S. 743–756.
- ↑ R. Tomaschek: Über Versuche zur Auffindung elektrodynamischer Wirkungen der Erdbewegung in großen Höhen II. In: Annalen der Physik. 80, 1926, S. 509–514.
- ↑ Carl T. Chase: A Repetition of the Trouton-Noble Ether Drift Experiment. In: Physical Review. 28, Nr. 2, 1926, S. 378-383. doi:10.1103/PhysRev.28.378.
- ↑ Carl T. Chase: The Trouton–Noble Ether Drift Experiment. In: Physical Review. 30, Nr. 4, 1927, S. 516–519. doi:10.1103/PhysRev.30.516.
- ↑ R. Tomaschek: Bemerkung zu meinen Versuchen zur Auffindung elektrodynamischer Wirkungen in großen Höhen. In: Annalen der Physik. 84, 1927, S. 161–162.
- ↑ H. C. Hayden: High sensitivity Trouton–Noble experiment. In: Rev. Scientific Instruments. 65, Nr. 4, 1994, S. 788–792. doi:10.1063/1.1144955.
- ↑ Lewis, Gilbert N. & Tolman, Richard C.: The Principle of Relativity, and Non-Newtonian Mechanics. In: Proceedings of the American Academy of Arts and Sciences. 44, 1909, S. 709–726.
- ↑ a b Laue, Max von: Ein Beispiel zur Dynamik der Relativitätstheorie. In: Verhandlungen der Deutschen Physikalischen Gesellschaft. 13, 1911, S. 513-518.
- ↑ Lorentz, Hendrik Antoon: Elektromagnetische Erscheinungen in einem System, das sich mit beliebiger, die des Lichtes nicht erreichender Geschwindigkeit bewegt. In: Blumenthal, Otto & Sommerfeld, Arnold (Hrsg.): Das Relativitätsprinzip. Eine Sammlung von Abhandlungen, S. 6-26 1904
- ↑ Laue, Max von: Zur Dynamik der Relativitätstheorie. In: Annalen der Physik. 340, Nr. 8, 1911, S. 524-542. doi:10.1002/andp.19113400808.
- ↑ Laue, Max von: Bemerkungen zum Hebelgesetz in der Relativitätstheorie. In: Physikalische Zeitschrift. 12, 1911, S. 1008-1010.
- ↑ Laue, Max von: Zur Theorie des Versuches von Trouton und Noble. In: Annalen der Physik. 343, Nr. 7, 1912, S. 370-384. doi:10.1002/andp.19123430705.
- ↑ Epstein, P. S.: Über relativistische Statik. In: Annalen der Physik. 341, Nr. 14, 1911, S. 779-795. Bibcode: 1911AnP...341..779E. doi:10.1002/andp.19113411404.
- ↑ Epstein, P. S.: Conference on the Michelson-Morley experiment. In: Contributions from the Mount Wilson Observatory. 373, 1927, S. 45-49. Bibcode: 1928CMWCI.373...43E.
Literatur
- Michel Janssen, "A comparison between Lorentz's ether theory and special relativity in the light of the experiments of Trouton and Noble, Ph.D. thesis (1995). Online: TOC, pref., intro-I, 1, 2, intro-II, 3, 4, refs.
- Tolman, R.C.: The Right-Angled Lever. In: The theory of relativity of motion, S. 152-153, Berkeley: University of California press 1917
- Pauli, Wolfgang: Anwendung auf spezielle Fälle. Versuch von Trouton-Noble. In: Die Relativitätstheorie, 5, S. 685-689 1921
- Butler, J. W.: On the Trouton-Noble Experiment. In: American Journal of Physics. 36, Nr. 11, 1968, S. 936–941. Bibcode: 1968AmJPh..36..936B. doi:10.1119/1.1974358.
- Aranoff, S.: Torques and Angular Momentum on a System at Equilibrium in Special Relativity. In: American Journal of Physics. 37, Nr. 4, 1969, S. 453-454. doi:10.1119/1.1975612.
- Furry, W. H.: Examples of Momentum Distributions in the Electromagnetic Field and in Matter. In: American Journal of Physics. 37, Nr. 6, 1969, S. 621-636. doi:10.1119/1.1975729.
- Newburgh, R. G.: The relativistic problem of the right-angled lever: The correctness of the Laue solution. In: Il Nuovo Cimento B. 61, Nr. 2, 1969, S. 201-209. doi:10.1007/BF02710928.
- Butler, J. W.: The Lewis-Tolman Lever Paradox. In: American Journal of Physics. 38, Nr. 3, 1970, S. 360-368. doi:10.1119/1.1976326.
- Aranoff, S.: Equilibrium in special relativity. In: Il Nuovo Cimento B. 10, Nr. 1, 1972, S. 155–171. Bibcode: 1972NCimB..10..155A. doi:10.1007/BF02911417.
- Sears, Francis W.: Another Relativistic Paradox. In: American Journal of Physics. 40, Nr. 5, 1972, S. 771-773. doi:10.1119/1.1986643.
- Aranoff, S.: More on the Right-Angled Lever at Equilibrium in Special Relativity. In: American Journal of Physics. 41, Nr. 9, 1973, S. 1108-1109. doi:10.1119/1.1987485.
- Grøn, Ø.: The asynchronous formulation of relativistic statics and thermodynamics. In: Il Nuovo Cimento B. 17, Nr. 1, 1973, S. 141-165. doi:10.1007/BF02906436.
- Nickerson, J. Charles; McAdory, Robert T.: The Trouton-Noble paradox. In: American Journal of Physics. 43, Nr. 7, 1975, S. 615-621. doi:10.1119/1.9761.
- Grøn, Ø.: Relativistics statics and F. W. Sears. In: American Journal of Physics. 46, Nr. 3, 1978, S. 249-250. doi:10.1119/1.11164.
- Cavalleri, G.; Grøn, Ø.; Spavieri, G.; Spinelli, G.: Comment on the article "Right-angle lever paradox" by J. C. Nickerson and R. T. McAdory. In: American Journal of Physics. 46, Nr. 1, 1978, S. 108-109. doi:10.1119/1.11106.
- Holstein, Barry R.; Swift, Arthur R.: Flexible string in special relativity. In: American Journal of Physics. 50, Nr. 10, 1982, S. 887-889. doi:10.1119/1.13002.
- Aguirregabiria, J. M.; Hernandez, A.; Rivas, M.: A Lewis-Tolman-like paradox. In: European Journal of Physics. 3, Nr. 1, 1982, S. 30-33. doi:10.1088/0143-0807/3/1/008.
- Prokhovnik, S. J.; Kovács, K. P.: The application of special relativity to the right-angled lever. In: Foundations of Physics. 15, Nr. 2, 1985, S. 167-173. doi:10.1007/BF00735288.
- Singal, Ashok K.: On the "explanation" of the null results of Trouton-Noble experiment. In: American Journal of Physics. 61, Nr. 5, 1993, S. 428–433. Bibcode: 1993AmJPh..61..428S. doi:10.1119/1.17236.
- Teukolsky, Saul A.: The explanation of the Trouton-Noble experiment revisited. In: American Journal of Physics. 64, Nr. 9, 1996, S. 1104–1109. Bibcode: 1996AmJPh..64.1104T. doi:10.1119/1.18329.
- Jefimenko, Oleg D.: The Trouton-Noble paradox. In: Journal of Physics A. 32, Nr. 20, 1999, S. 3755–3762. Bibcode: 1999JPhA...32.3755J. doi:10.1088/0305-4470/32/20/308.
- Jackson, J. D.: Torque or no torque? Simple charged particle motion observed in different inertial frames. In: American Journal of Physics. 72, Nr. 12, 2004, S. 1484-1487. doi:10.1119/1.1783902.
- Ivezić, Tomislav: Axiomatic Geometric Formulation of Electromagnetism with Only One Axiom: The Field Equation for the Bivector Field F with an Explanation of the Trouton-Noble Experiment. In: Foundations of Physics Letters. 18, Nr. 5, 2005, S. 401-429. doi:10.1007/s10702-005-7533-7. arXiv:physics/0412167.
- Franklin, Jerrold: The lack of rotation in the Trouton Noble experiment. In: European Journal of Physics. 27, Nr. 5, 2006, S. 1251–1256. Bibcode: 2006EJPh...27.1251F. doi:10.1088/0143-0807/27/5/024. arXiv:physics/0603110.
- Ivezić, Tomislav: Trouton Noble Paradox Revisited. In: Foundations of Physics. 37, Nr. 4–5, 2006, S. 747–760. Bibcode: 2007FoPh...37..747I. doi:10.1007/s10701-007-9116-x. arXiv:physics/0606176.
Weblinks
- Kevin Brown, "Trouton-Noble and The Right-Angle Lever auf MathPages.
- Michel Janssen, "The Trouton Experiment and E = mc2," Einstein for Everyone Kurs der UMN (2002).
Isotropie von c: Michelson-Morley-Experiment | Kennedy-Thorndike-Experiment | Mößbauer-Rotor-Experiment | Resonator-Experimente
Lorentzinvarianz: Hughes-Drever-Experiment | Moderne Tests der Lorentzinvarianz |Trouton-Noble-Experiment | Experimente von Rayleigh und Brace | Trouton-Rankine-Experiment |
Zeitdilatation: Ives-Stilwell-Experiment | Mößbauer-Rotor-Experiment | Zeitdilatation bewegter Teilchen
Sagnac/Fizeau: Sagnac-Experiment | Fizeau-Experiment
Relativistische Energie: Kaufmann-Bucherer-Neumann-Experimente | Teilchenbeschleuniger
Alternativen: Widerlegungen der Äthertheorie | Widerlegungen der Emissionstheorie
Allgemein: Testtheorien | Standardmodellerweiterung | Einweg-Lichtgeschwindigkeit
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Trouton–Noble experiment — The Trouton–Noble experiment attempted to detect motion of the Earth through the luminiferous aether, and was conducted in 1901 ndash;1903 by Frederick Thomas Trouton (who also developed the Trouton s ratio) and H. R. Noble. It was based on a… … Wikipedia
Trouton–Rankine-Experiment — Mit dem Trouton Rankine Experiment (1908) sollte festgestellt werden, ob die Längenkontraktion von einem mitbewegten Beobachter gemessen werden kann, wodurch eine Relativbewegung zum Äther (Ätherwind) bewiesen wäre. Das Experiment ging negativ… … Deutsch Wikipedia
Trouton-Rankine-Experiment — Mit dem Trouton Rankine Experiment (1908) sollte festgestellt werden, ob die Längenkontraktion von einem mitbewegten Beobachter gemessen werden kann, wodurch eine Relativbewegung zum Äther (Ätherwind) bewiesen wäre. Das Experiment ging negativ… … Deutsch Wikipedia
Trouton–Rankine experiment — The Trouton–Rankine experiment was an experiment designed to measure if the Lorentz–FitzGerald contraction of an object according to one frame (as defined by the luminiferous aether) produced a measurable effect in the rest frame of the object,… … Wikipedia
Expérience de Trouton-Noble — L’expérience de Trouton Noble est une tentative de détecter le déplacement de la Terre dans l éther. Cette expérience fut menée de 1901 à 1903 par Frederick Thomas Trouton et Henry R. Noble. Elle est liée à quelques expériences de pensée :… … Wikipédia en Français
Trouton — Frederick Thomas Trouton. Frederick Thomas Trouton (* 24. November 1863 in Dublin; † 21. September 1922 in Downe) war ein irischer Experimentalphysiker. Bekannt wurde Trouton durch die Pictet Trouton Regel, das Trouton Noble E … Deutsch Wikipedia
Michelson-Experiment — Wenn elektromagnetische Wellen an einen ruhenden Äther gebunden wären, müsste man die Eigenbewegung von Erde und Sonne als Ätherwind messen können. Das Michelson Morley Experiment war ein physikalisches Experiment, das von dem deutsch… … Deutsch Wikipedia
Frederick Thomas Trouton — Frederick Thomas Trouton. Frederick Thomas Trouton (* 24. November 1863 in Dublin; † 21. September 1922 in Downe) war ein irischer Experimentalphysiker. Bekannt wurde Trouton durch die Pictet Trouton Regel, das Trouton Noble Experiment sowie das… … Deutsch Wikipedia
Michelson–Morley experiment — Box plots based on data from the Michelson–Morley experiment The Michelson–Morley experiment was performed in 1887 by Albert Michelson and Edward Morley at what is now Case Western Reserve University in Cleveland, Ohio. Its results are generally… … Wikipedia
Hammar experiment — The Hammar experiment was an experiment designed by Gustaf Wilhelm Hammar to test the aether drag hypothesis.OverviewIn 1903 the Trouton Noble experiment, and later the Trouton Rankine experiment in 1908, presented (then) controversial evidence… … Wikipedia