- Turingmodell
-
Die Turingmaschine ist ein von dem britischen Mathematiker Alan Turing 1936 entwickeltes Modell, um eine Klasse von berechenbaren Funktionen zu bilden. Sie gehört zu den grundlegenden Konzepten der Informatik.
Das Modell wurde im Rahmen des von David Hilbert im Jahr 1920 formulierten Hilbertprogramms, speziell zur Lösung des so genannten Entscheidungsproblems, in der Schrift "On Computable Numbers, with an Application to the Entscheidungsproblem" vorgestellt. Alan Turing beabsichtigte, mit der Turingmaschine ein Modell des mathematisch arbeitenden Menschen zu schaffen.
Das Besondere an einer Turingmaschine ist, dass sie mit nur drei Operationen (Lesen, Schreiben und Kopf bewegen) alle Probleme lösen kann, die auch von einem Computer gelöst werden können. Sämtliche mathematischen Grundfunktionen wie Addition und Multiplikation lassen sich mit diesen drei Operationen simulieren. Darauf aufbauend kann man dann komplexe Operationen der üblichen Computerprogramme simulieren. Eine Funktion, die so durch eine Turingmaschine berechnet werden kann, nennt man eine turingberechenbare Funktion.
Die Church-Turing-These stellt die Behauptung auf, dass eine Turingmaschine gerade die von Menschen berechenbaren mathematischen Funktionen lösen kann. Daraus darf jedoch nicht gefolgert werden, dass eine Turingmaschine alle mathematischen Funktionen lösen kann. So kann etwa anhand des Halteproblems gezeigt werden, dass es mathematische Funktionen gibt, die nicht von Turingmaschinen (und daher gemäß Church-Turing-These auch nicht von Menschen) berechnet werden können.
Inhaltsverzeichnis
Informelle Beschreibung
Die Turingmaschine besteht aus
- einem unendlich langen Speicherband mit unendlich vielen sequentiell angeordneten Feldern. In jedem dieser Felder ist zu jedem Zeitpunkt genau ein Zeichen gespeichert. Dabei ist als Zeichen ein Blanksymbol zugelassen, was so viel bedeutet wie „leeres Feld“. Das Blanksymbol gehört nicht zu der Menge der Eingabezeichen. Man darf sich das unendlich lange Band auch als ein endliches vorstellen, es muss jedoch lang genug sein, um die aktuelle Berechnung ungehindert ausführen zu können, d. h. der Lese- und Schreibkopf darf nicht an das Ende stoßen.
- einem programmgesteuerten Lese- und Schreibkopf, der sich auf dem Speicherband feldweise bewegen und die Zeichen verändern kann.
Die Turingmaschine modifiziert die Eingabe auf dem Band nach einem gegebenen Programm. Die Startposition der Turingmaschine ist am Anfang des Eingabeworts, d. h. an der Position des ersten Eingabezeichens, wenn man von links nach rechts liest.
Mit jedem Schritt liest der Lese-/Schreibkopf das aktuelle Zeichen, überschreibt dieses mit einem anderen (oder dem gleichen) Zeichen und bewegt sich dann ein Feld nach links oder rechts oder bleibt stehen. Welches Zeichen geschrieben wird und welche Bewegung ausgeführt wird, hängt von dem an der aktuellen Position vorgefundenen Zeichen sowie dem Zustand ab, in dem sich die Turingmaschine gerade befindet. Dies wird durch eine zu der Turingmaschine gehörende Funktion definiert. Zu Beginn befindet sich die Turingmaschine in einem vorgegebenen Startzustand und geht bei jedem Schritt in einen neuen Zustand über. Ein Zustand kann mehrere Male durchlaufen werden, er sagt nichts über die auf dem Band vorliegenden Zeichen aus.
Man kann bestimmte Zustände der Turingmaschine als Endzustände definieren. Sobald die Maschine in einen dieser Zustände kommt, bleibt sie stehen, unabhängig davon, welches Zeichen sich an der aktuellen Position befindet. Es gibt Eingaben, für die eine Turingmaschine niemals stoppt.
Die Turingmaschine wird (wie viele andere Automaten) auch für Entscheidungsprobleme eingesetzt, also für Fragen, die mit „ja“ oder „nein“ zu beantworten sind. Hierbei werden zum Beispiel zwei Zeichen vereinbart, wobei das eine als „ja“ und das andere als „nein“ interpretiert wird. Nach dem Anhalten der Turingmaschine liegt die Antwort als eines der beiden Zeichen auf dem Ausgabeband vor. Zu beachten ist dabei, dass sich jedes Problem als Entscheidungsproblem formulieren lässt, indem man fragt, ob ein bestimmter Wert eine Lösung für ein konkretes Problem ist.
Formale Definition
Formal kann eine deterministische Turingmaschine als 7-Tupel
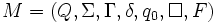 dargestellt werden (siehe auch nichtdeterministische Turingmaschine).
dargestellt werden (siehe auch nichtdeterministische Turingmaschine).- Q ist die endliche Zustandsmenge
- Σ ist das endliche Eingabealphabet
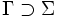 ist das endliche Bandalphabet
ist das endliche Bandalphabet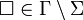 steht für das leere Feld
steht für das leere Feld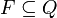 ist die Menge der End- bzw. akzeptierenden Zustände
ist die Menge der End- bzw. akzeptierenden Zustände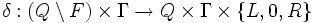 ist die Überführungsfunktion
ist die Überführungsfunktion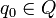 ist der Anfangszustand
ist der Anfangszustand
Die Turingmaschine führt eine Berechnung aus, indem sie schrittweise eine Eingabe in eine Ausgabe umwandelt. Ein-, Ausgabe und Zwischenergebnisse werden auf dem unendlich langen Band gespeichert.Zu Beginn steht ein Wort als Eingabe auf dem Band (pro Bandfeld ein Zeichen des Eingabewortes), der Rest des Bandes ist mit dem leeren Feld „formatiert“. Der Schreib-/Lesekopf steht auf dem ersten Zeichen der Eingabe und die TM befindet sich im (Start-)Zustand q0.
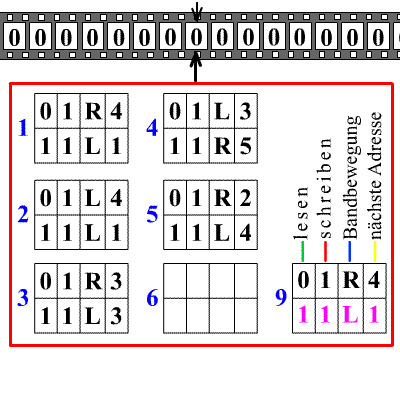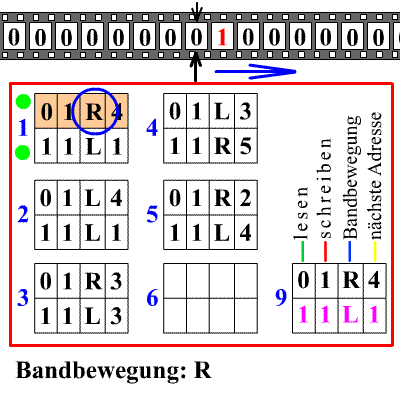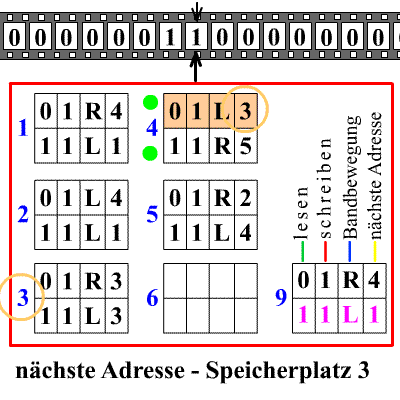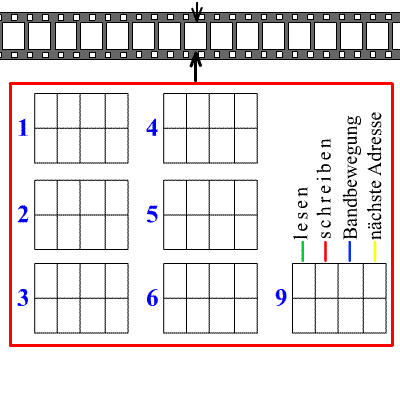
Die Überführungsfunktion gibt an, wie die Turingmaschine schrittweise den Bandinhalt, ihren Zustand und die Position des Schreib-/Lesekopfes ändert. Diese Funktion nimmt als Argument den aktuellen Zustand und das Zeichen, das sich im aktuellen Schritt unter dem Schreib-/Lesekopf befindet. Als Ergebnis liefert sie dann genau einen Zustand (dieser wird dann der Nachfolgezustand der Turingmaschine), ein Zeichen (mit diesem Zeichen wird dann der Inhalt des Feldes, auf das der Schreib-/Lesekopf weist, überschrieben) und entweder das Symbol L (in diesem Fall bewegt sich der Schreib-/Lesekopf um ein Feld nach links), ein R (in diesem Fall bewegt er sich ein Feld nach rechts) oder eine 0 (dann verharrt er auf demselben Feld). Damit hat die Turingmaschine einen Schritt ihres Arbeitszyklus' durchlaufen und steht für einen weiteren bereit.
Erreicht die Turingmaschine einen Endzustand, also einen Zustand der Menge F, ist die Berechnung beendet. Die Ausgabe ist dann der Inhalt des Bandes (wobei die Felder, die mit Symbolen aus
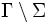 gefüllt sind, insbesondere dem Symbol
gefüllt sind, insbesondere dem Symbol  , nicht berücksichtigt werden).
, nicht berücksichtigt werden).Je nach Bandalphabet können Ein-/Ausgaben und Zwischenspeicherungen unterschiedlich kenntlich gemacht werden.
Beispiel
Die folgende deterministische 1-Band-Turingmaschine M erwartet eine Folge von Einsen als Eingabe auf dem Band. Sie verdoppelt die Anzahl der Einsen, wobei ein Leersymbol in der Mitte stehen bleibt. Aus "111" wird beispielsweise die Zeichenfolge "1110111". Der Schreib-/Lesekopf befindet sich initial auf der ersten Eins. Der Anfangszustand ist s1, der Endzustand s6. Die Null steht für das leere Feld und das Band ist bis auf die daraufgeschriebenen Einsen mit leeren Feldern gefüllt.
M = (Q,Σ,Γ,δ,s1,0,F)
- Q = {s1,s2,s3,s4,s5,s6}
- Σ = {1}
- Γ = {1,0}
- F = {s6}
aktueller
Zustandgeles.
Symbolschr.
Symbolneuer
ZustandKopf-
richtungs1 1 → 0 s2 R s1 0 → 0 s6 0 s2 1 → 1 s2 R s2 0 → 0 s3 R s3 0 → 1 s4 L s3 1 → 1 s3 R s4 1 → 1 s4 L s4 0 → 0 s5 L s5 1 → 1 s5 L s5 0 → 1 s1 R M durchläuft zum Beispiel bei der Eingabe "11" folgende Zustände, wobei die aktuelle Kopfposition fett gedruckt ist:
Schritt Zust. Band 1 s1 11000 2 s2 01000 3 s2 01000 4 s3 01000 5 s4 01010 6 s5 01010 7 s5 01010 8 s1 11010 Schritt Zust. Band 9 s2 10010 10 s3 10010 11 s3 10010 12 s4 10011 13 s4 10011 14 s5 10011 15 s1 11011 16 s6 -halt- Die Berechnung beginnt im Anfangszustand s1. Hier wird die erste Eins durch ein leeres Feld ersetzt, der Schreib-/Lesekopf bewegt sich nach rechts und neuer Zustand wird s2. Der Kopf wandert nun solange nach rechts, bis ein leeres Feld gelesen wird. Danach gelangt die Turingmaschine in den Zustand s3 und überliest alle weiteren Einsen, bis sie erneut ein leeres Feld findet. Dieses wird dann durch eine Eins ersetzt. Im Zustand s4 bewegt sich der Kopf zurück, überliest wieder alle Einsen, bis er auf ein leeres Feld trifft, Zustandswechsel auf s5. Der Kopf bewegt sich nun solange nach links, bis das ursprünglich in Zustand s1 geschriebene leere Feld gefunden wird. Dieses wird wieder durch eine Eins ersetzt, der Kopf bewegt sich ein Feld nach rechts und die Turingmaschine gelangt wieder in den Zustand s1. Hier beginnt ein neuer Rechenzyklus.
Wird im Zustand s1 ein leeres Feld gelesen, so gelangt die Turingmaschine M in den Endzustand s6, woraufhin die Berechnung beendet wird.Variationen des Turingmaschinen-Modells
Überblick über Variationsmöglichkeiten
In der Literatur findet man zahlreiche unterschiedliche Definitionen der Turingmaschine, die sich jeweils in einigen Details unterscheiden. So variiert etwa die Anzahl der Bänder, das verwendete Bandalphabet, die zusätzlich verwendeten Spezialzeichen und andere Eigenschaften. Die Vielfalt ist theoretisch durch die These von Church gerechtfertigt, welche im Hinblick auf die Berechenbarkeit die Äquivalenz aller universellen Maschinenmodelle postuliert. Selbst komplexitätstheoretisch sind die Unterschiede zwischen verschiedenen Definitionen weitgehend zu vernachlässigen. So lässt sich etwa jede f(n)-zeitbeschränkte k-Bandmaschine mit beliebig großem k durch eine nur O(f²(n))-zeitbeschränkte 1-Bandmaschine simulieren. Für die Simulation beliebig vieler Bänder kommt es also zu einem maximal quadratischen Mehraufwand. Insgesamt führen alle Arten von Variationen zu nicht mehr als polynomialen Aufwandsunterschieden (wobei Aufwand hier eine beliebige Ressource meint) und sind daher für viele komplexitätstheoretische Untersuchungen vernachlässigbar. Man passt in Abhängigkeit von den Zielen der jeweiligen Analyse das verwendete Modell so an, dass die Analyse möglichst einfach durchgeführt werden kann. Folgende Beispiele zeigen Anwendungen und Variationen des Turingmaschinen-Modells.
Universelle Turingmaschine
In der obigen Definition ist das Programm fest in die Maschine eingebaut und kann nicht verändert werden. Man kann aber eine universelle Turingmaschine definieren, welche die Kodierung einer Turingmaschine als Teil ihrer Eingabe nimmt, und das Verhalten der kodierten Turingmaschine auf der ebenfalls gegebenen Eingabe simuliert. Aus der Existenz einer solchen universellen Turingmaschine folgt zum Beispiel die Unentscheidbarkeit des Halteproblems. Eine ähnliche Idee, bei der das Programm als ein Teil der veränderbaren Eingabedaten betrachtet wird, liegt auch fast allen heutigen Rechnerarchitekturen zugrunde (Von-Neumann-Architektur).
Formal ist eine universelle Turingmaschine eine Maschine UTMφ, die eine Eingabe
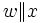 liest. Das Wort w ist hierbei eine beliebige Beschreibung einer Maschine Mw, die zu einer bestimmten Funktion mit Eingabe x die Ausgabe berechnet.
liest. Das Wort w ist hierbei eine beliebige Beschreibung einer Maschine Mw, die zu einer bestimmten Funktion mit Eingabe x die Ausgabe berechnet. 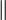 ist ein Trennzeichen zwischen Programmbeschreibung und Eingabe. UTMφ simuliert also das Verhalten von Mw mit Hilfe der Funktionsbeschreibung w und der Eingabe x. Der Index φ in UTMφ zeigt an, dass es nicht nur eine einzige universelle Turingmaschine gibt. So könnten z.B. UTM1 und UTM2 verschiedene Wörter verstehen. Das Wort w muss dabei in einer Sprache codiert sein, die die UTMφ versteht.
ist ein Trennzeichen zwischen Programmbeschreibung und Eingabe. UTMφ simuliert also das Verhalten von Mw mit Hilfe der Funktionsbeschreibung w und der Eingabe x. Der Index φ in UTMφ zeigt an, dass es nicht nur eine einzige universelle Turingmaschine gibt. So könnten z.B. UTM1 und UTM2 verschiedene Wörter verstehen. Das Wort w muss dabei in einer Sprache codiert sein, die die UTMφ versteht.Persistente Turingmaschine
Um interaktive Modelle (im Sinne von "Modellen mit Gedächtnis") durch eine Turingmaschine darzustellen, ist eine Erweiterung derselben um eben dieses Gedächtnis notwendig.
Laut Definition (Goldin et al., 2003: Turing Machines, Transition Systems and Interaction) ist eine Persistente Turingmaschine (PTM) eine nichtdeterministische 3-Band-Turingmaschine mit einem Input-, einem Arbeits- und einem Output-Band. Der Input wird auf dem Arbeits-Band verarbeitet und erst nach vollständiger Bearbeitung gelangen die Ergebnisse auf dem Output-Band zurück in die "Umwelt". Danach kann ein erneuter Input aus der Umwelt verarbeitet werden. Zwischen zwei Arbeitsschritten bleiben die Inhalte des Arbeits-Bandes als "Gedächtnis" erhalten.
Ameise
Chris Langtons Ameise ist eine Turingmaschine mit zweidimensionalem Band, sehr einfachen Regeln und verblüffenden Ergebnissen. (Siehe Ameise (Turingmaschine))
Fleißiger Biber
Ein beliebtes Problem ist der Fleißige Biber: Man finde die Turingmaschine, die mit einer bestimmten Anzahl von Zuständen die maximale Anzahl eines bestimmten Symbols (meist "1") auf das Band schreibt und dann anhält (d.h. eine Endlosschleife ist ausgeschlossen).
Vergessliche Turingmaschine
Eine Turingmaschine wird vergesslich[1] genannt, falls die Kopfbewegungen nicht vom Inhalt der Eingabe abhängen. Jede Turingmaschine kann durch eine vergessliche simuliert werden [2].
Beziehung zwischen einer Turingmaschine und einer formalen Sprache
Akzeptierte Sprache
Eine Turingmaschine akzeptiert eine Sprache L, wenn sie bei Eingabe eines jeden Wortes
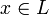 nach endlich vielen Schritten in einen der definierten Endzustände übergeht. Wenn die Turingmaschine in einem anderen Zustand hält oder überhaupt nicht, dann wird die Eingabe x von ihr nicht akzeptiert.
nach endlich vielen Schritten in einen der definierten Endzustände übergeht. Wenn die Turingmaschine in einem anderen Zustand hält oder überhaupt nicht, dann wird die Eingabe x von ihr nicht akzeptiert.Eine Sprache
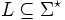 heißt genau dann rekursiv aufzählbar bzw. semientscheidbar (Typ 0 der Chomsky-Hierarchie), wenn es eine deterministische Turingmaschine gibt, die L akzeptiert.
heißt genau dann rekursiv aufzählbar bzw. semientscheidbar (Typ 0 der Chomsky-Hierarchie), wenn es eine deterministische Turingmaschine gibt, die L akzeptiert.Entscheidbare Sprache
Akzeptiert eine Turingmaschine eine Sprache und hält sie zusätzlich bei allen Eingaben, die nicht zu dieser Sprache gehören, so entscheidet die Turingmaschine diese Sprache.
Eine Sprache
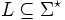 heißt rekursiv oder entscheidbar, wenn es eine deterministische Turingmaschine gibt, die L entscheidet.
heißt rekursiv oder entscheidbar, wenn es eine deterministische Turingmaschine gibt, die L entscheidet.Siehe auch
Literatur
- Oswald Wiener, Manuel Bonik, Robert Hödicke: Eine elementare Einführung in die Theorie der Turing-Maschinen, Wien / New York: Springer-Verlag 1998, ISBN 3-211-82769-2
- Turing, A., On Computable Numbers, With an Application to the Entscheidungsproblem, Proceedings of the London Mathematical Society, Series 2, Volume 42, 1936; reprinted in M. David (ed.), The Undecidable, Hewlett, NY: Raven Press, 1965
- Sybille Krämer, Symbolische Maschinen. Die Idee der Formalisierung im geschichtlichen Abriß, Darmstadt: Wissenschaftliche Buchgesellschaft 1988
- Rolf Herken: The Universal Turing Machine - A Half-Century Survey, Wien / New York: Springer Verlag, ISBN 3-211-82637-8
- Heinz Lüneburg: Rekursive Funktionen, Springer-Verlag, ISBN 3-540-43094-6
- Marvin Minsky: Computation: Finite and Infinite Machines, Englewood Cliffs, N.J.: Prentice-Hall 1967
- B.A. Trachtenbrot: Algorithmen und Rechenautomaten, Berlin: VEB Deutscher Verlag der Wissenschaften 1977
Weblinks
- Eintrag in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
- Die Turing-Maschine
- Varianten universeller Turingmaschinen
- A Turing Machine In Conway's Game of Life
Einzelnachweise
- ↑ auf englisch: oblivious, http://www.cs.princeton.edu/theory/complexity/, Abschnitt 2.3.4
- ↑ http://www.cs.princeton.edu/theory/complexity/, Remark 1.10
Wikimedia Foundation.