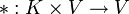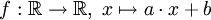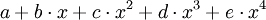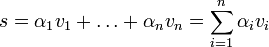- Unitärer Vektorraum
-
Vektorraum berührt die Spezialgebiete
ist Spezialfall von
umfasst als Spezialfälle
- Körper (VR über sich selbst)
- topologischer Vektorraum
- Algebra (mit innerer Multiplikation)
Ein Vektorraum oder linearer Raum ist eine algebraische Struktur, die in fast allen Zweigen der Mathematik verwendet wird. Eingehend betrachtet werden Vektorräume in der Linearen Algebra.
Die einzelnen Elemente eines Vektorraums heißen Vektoren. Addiert man Vektoren oder multipliziert sie mit einer skalaren Zahl, dann ist das Ergebnis wieder ein Vektor desselben Vektorraums. Vektoren können nicht nur die aus der Geometrie bekannten Gebilde sein, sondern auch abstraktere Objekte wie Funktionen oder Matrizen.
Da die skalaren Zahlen, mit denen man einen Vektor multiplizieren kann, einem Körper entstammen, ist ein Vektorraum immer ein Vektorraum „über“ einem bestimmten Körper. Man spricht beispielsweise von einem Vektorraum über den reellen Zahlen. In den meisten Anwendungen legt man diese oder die komplexen Zahlen zugrunde.
Eine Basis eines Vektorraums ist eine Menge von Vektoren, die es erlaubt, jeden Vektor durch eindeutige Koordinaten zu beschreiben. Wird mit Vektoren gerechnet, so wird mit deren Koordinaten gerechnet. Die Anzahl der Basisvektoren wird Dimension des Vektorraums genannt. Sie ist unabhängig von der Wahl der Basis und kann auch unendlich sein.
Inhaltsverzeichnis
Formale Definition
Ein Vektorraum über einem Körper
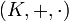 oder kurz K-Vektorraum ist eine additive abelsche Gruppe (V, + ), auf der zusätzlich eine Multiplikation mit einem Skalar aus K erklärt ist:
oder kurz K-Vektorraum ist eine additive abelsche Gruppe (V, + ), auf der zusätzlich eine Multiplikation mit einem Skalar aus K erklärt ist:Diese Skalarmultiplikation muss dabei für alle
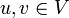 und
und 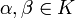 die folgenden Bedingungen erfüllen:
die folgenden Bedingungen erfüllen:- I:
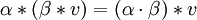
- IIa: α * (u + v) = α * u + α * v
- IIb: (α + β) * v = α * v + β * v,
sowie die Neutralität der 1 (als Einselement) des Körpers K
- III:1 * v = v
Anders ausgedrückt ist ein K-Vektorraum ein unitärer K-Linksmodul, dessen Grundring K ein (kommutativer) Körper ist.
Anmerkungen
- Die Addition der abelschen Gruppe (V, + ) heißt Vektoraddition, ihr neutrales Element Nullvektor.
- In Analogie zu den Axiomen eines Körpers werden die Vektorraumaxiome I und II häufig als Assoziativitäts-, beziehungsweise Distributivgesetze bezeichnet.[1][2] Dabei ist jedoch zu beachten, dass bei I die Skalarmultiplikation assoziativ mit der Multiplikation in K ist, und dass in IIb die Pluszeichen zwei verschiedene Additionen (links die in K bzw. rechts jene in V) bezeichnen.
- Die zu Distributivgesetzen analogen Axiome IIa und IIb garantieren die Verträglichkeit von Vektoraddition und Skalarmultiplikation.
- In diesem Artikel wird die Skalarmultiplikation zur besseren Unterscheidung mit „ * “ bezeichnet. Obwohl die Multiplikation im Körper K und die Skalarmultiplikation nicht verwechselt werden dürfen, werden sie in der Praxis jedoch zumeist beide mit demselben Zeichen „
 “ bezeichnet. Oft lässt man das Multiplikationszeichen sogar ganz weg. Ähnlich wurden bereits oben die Addition in der abelschen Gruppe V und die Addition im Körper K durch dasselbe Symbol „ + “ bezeichnet, obwohl sie streng genommen zu unterscheiden wären. Die Verwendung der gleichen Symbole macht andererseits die Vektorraumaxiome besonders suggestiv.
“ bezeichnet. Oft lässt man das Multiplikationszeichen sogar ganz weg. Ähnlich wurden bereits oben die Addition in der abelschen Gruppe V und die Addition im Körper K durch dasselbe Symbol „ + “ bezeichnet, obwohl sie streng genommen zu unterscheiden wären. Die Verwendung der gleichen Symbole macht andererseits die Vektorraumaxiome besonders suggestiv.
Alternative Definition
Ist (V, + ) eine abelsche Gruppe, so bilden die Endomorphismen hiervon mit punktweiser Addition als Addition und der Komposition von Abbildungen als Multiplikation einen Ring
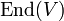 (mit der Identität als Einselement). Ist K ein Körper, der auf V operiert, d. h. hat man einen Homomorphismus
(mit der Identität als Einselement). Ist K ein Körper, der auf V operiert, d. h. hat man einen Homomorphismus 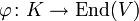 von Ringen mit Einselement, so macht dies V zu einem K-Vektorraum.
von Ringen mit Einselement, so macht dies V zu einem K-Vektorraum.Die Äquivalenz zu obenstehender Definition ergibt sich, wenn man
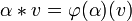 setzt.
setzt.Erste Eigenschaften
Für alle
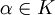 und
und 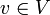 gelten folgende Sätze:
gelten folgende Sätze:- ( − α) * v = − (α * v) = α * ( − v).
 .
.
Die Gleichung v + x = w ist für alle
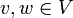 eindeutig lösbar; die Lösung ist x = w + ( − v).
eindeutig lösbar; die Lösung ist x = w + ( − v).Beispiele
Euklidische Ebene
Ein anschaulicher Vektorraum ist die zweidimensionale Euklidische Ebene
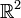 (in rechtwinkligen kartesischen Koordinaten) mit den Pfeilklassen (Verschiebungen oder Translationen) als Vektoren und den reellen Zahlen als Skalaren.
(in rechtwinkligen kartesischen Koordinaten) mit den Pfeilklassen (Verschiebungen oder Translationen) als Vektoren und den reellen Zahlen als Skalaren.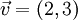 ist die Verschiebung um 2 Einheiten nach rechts und 3 Einheiten nach oben,
ist die Verschiebung um 2 Einheiten nach rechts und 3 Einheiten nach oben,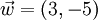 die Verschiebung um 3 Einheiten nach rechts und 5 Einheiten nach unten.
die Verschiebung um 3 Einheiten nach rechts und 5 Einheiten nach unten.
Die Summe zweier Verschiebungen ist wieder eine Verschiebung:
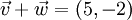 , d.h. 5 Einheiten nach rechts und 2 Einheiten nach unten.
, d.h. 5 Einheiten nach rechts und 2 Einheiten nach unten.
Der Nullvektor
 entspricht keiner Verschiebung, d. h. der identischen Abbildung.
entspricht keiner Verschiebung, d. h. der identischen Abbildung.Durch die Streckung der Verschiebung
 mit einem Skalar a = 3 aus der Menge der reellen Zahlen erhalten wir das Dreifache der Verschiebung:
mit einem Skalar a = 3 aus der Menge der reellen Zahlen erhalten wir das Dreifache der Verschiebung: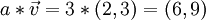 .
.
Alles zu diesem Beispiel gesagte gilt auch in der reellen affinen Ebene.
Raum der affinen Funktionen
Ein anderer Vektorraum ist der Raum der affinen Funktionen auf den reellen Zahlen. Dies sind die Funktionen der Form
mit reellen Zahlen a und b. Anschaulich gesprochen sind dies alle Funktionen, deren Graph eine Gerade ist. In dieser Anschauung erzeugt unser Raum alle Geraden bis auf die genau senkrecht stehenden. Wählen wir beispielhaft zwei affine Funktionen
- f(x) = 2x + 3 , g(x) = 3x − 5,
so sehen wir, wie deren Summe wieder eine affine Funktion ergibt:
- f(x) + g(x) = 2x + 3 + 3x − 5 = (2 + 3)x + (3 − 5) = 5x − 2
Der Nullvektor ist die konstante Funktion
- 0 = 0x + 0, die alle Punkte auf die Null abbildet.
Mit einem Skalar a = 3 aus der Menge der reellen Zahlen ergibt die Skalarmultiplikation
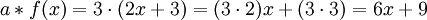 .
.
Vektorraum der Polynome
Die Polynome mit Koeffizienten aus einem Körper bilden, mit der üblichen Addition und der Multiplikation mit einem Element des Körpers, einen unendlich-dimensionalen Vektorraum. Für die Polynome, deren Grad durch ein
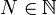 nach oben beschränkt ist, hat der resultierende Vektorraum die Dimension N + 1. Beispielsweise ist die Menge aller Polynome vom Grad kleiner gleich 4
nach oben beschränkt ist, hat der resultierende Vektorraum die Dimension N + 1. Beispielsweise ist die Menge aller Polynome vom Grad kleiner gleich 4ein Vektorraum der Dimension 5. Eine Basis bilden die Monome
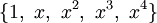 .
.Spezielle Vektorräume
- Euklidischer Vektorraum
- Ein euklidischer Vektorraum ist ein reeller Vektorraum mit Skalarprodukt. Er ist ein Spezialfall eines Prähilbertraums und auch Spezialfall eines Hilbertraums.
- Funktionenraum
- Ein Funktionenraum ist ein Vektorraum, dessen Elemente Funktionen sind. Funktionenräume sind Betrachtungsgegenstand der Funktionalanalysis und meist unendlichdimensional.
- Normierter Raum
- Ein normierter Raum ist ein Vektorraum, in dem Vektoren eine Länge (Norm) besitzen. Diese ist eine nichtnegative reelle Zahl und erfüllt die Dreiecksungleichung.
- Prähilbertraum
- Ein Prähilbertraum ist ein reeller oder komplexer Vektorraum, auf dem ein inneres Produkt (Skalarprodukt oder hermitesche Form) definiert ist. In einem solchen Raum kann man Begriffe wie Länge und Winkel definieren.
- Topologischer Vektorraum
- Ein topologischer Vektorraum über einem topologischen Körper K ist ein topologischer Raum V mit einer kompatiblen K-Vektorraumstruktur, d. h. die Vektorraumoperationen
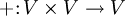 und
und  sind stetig.
sind stetig. - Unitärer Vektorraum
- Ein unitärer Vektorraum ist ein Vektorraum mit positiv definiter hermitescher Form. Er ist ein Spezialfall des Prähilbertraums.
In einem metrischen Raum ist das analytische Konzept der Konvergenz anwendbar; ein metrischer Raum, in dem jede Cauchy-Folge konvergiert, heißt vollständig. Ein vollständiger normierter Vektorraum heißt Banach-Raum, ein vollständiger Prähilbertraum heißt Hilbert-Raum.
Ein Tangentialraum enthält die lokale Vektorraumstruktur einer differenzierbaren Mannigfaltigkeit.
Aus einem Vektorraum und einem Untervektorraum kann man durch Bildung von Äquivalenzklassen einen weiteren Vektorraum, den Quotientenraum oder Faktorraum, bilden.
Untervektorraum
Ein Untervektorraum (auch linearer Unterraum) ist eine Teilmenge eines Vektorraums, die selbst wieder ein Vektorraum über demselben Körper ist. Dabei werden die Vektorraumoperationen auf den Untervektorraum vererbt.
Jeder Vektorraum enthält zwei triviale Untervektorräume, nämlich zum einen sich selbst, zum anderen den kleinsten Untervektorraum {0}, der nur aus dem Nullvektor besteht.
Kriterium für die Unterraumeigenschaft
Ist V ein K-Vektorraum, so bildet eine Teilmenge
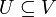 genau dann einen Untervektorraum, wenn die folgenden Bedingungen erfüllt sind:
genau dann einen Untervektorraum, wenn die folgenden Bedingungen erfüllt sind: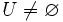
- für alle
 gilt
gilt 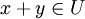
- (U ist abgeschlossen bezüglich der Vektoraddition)
- für alle
 und
und 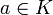 gilt
gilt 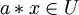
- (U ist abgeschlossen bezüglich der Skalarmultiplikation)
Beispiel
Es sei
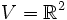 der Vektorraum der Paare reeller Zahlen. Ein Untervektorraum ist z. B.
der Vektorraum der Paare reeller Zahlen. Ein Untervektorraum ist z. B. 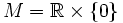 , da die drei obigen Voraussetzungen erfüllt sind. Anschaulich ist V eine Ebene, und M ist die mit der x-Achse zusammenfallende Gerade. Jede andere durch den Ursprung verlaufende Gerade ist ebenfalls ein Unterraum.
, da die drei obigen Voraussetzungen erfüllt sind. Anschaulich ist V eine Ebene, und M ist die mit der x-Achse zusammenfallende Gerade. Jede andere durch den Ursprung verlaufende Gerade ist ebenfalls ein Unterraum.Beweis der Gültigkeit des Unterraumkriteriums
Sei V ein K-Vektorraum und
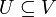 eine Teilmenge.
eine Teilmenge.Ist U mit den vererbten Operationen ebenfalls ein K-Vektorraum, so gelten auch die drei Teilkriterien: Die ersten beiden ergeben sich, weil (U, + ) eine Untergruppe von (V, + ) sein muss, das letzte, weil die Einschränkung von * die Skalarmultiplikation für U ist.
Sind umgekehrt die drei Teilkriterien erfüllt, so ist für jedes
 wegen des dritten Kriteriums stets auch das additive Inverse
wegen des dritten Kriteriums stets auch das additive Inverse 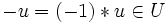 , so dass zusammen mit den ersten beiden folgt, dass (U, + ) eine Untergruppe von (V, + ), insb. also eine abelsche Gruppe ist. Da obendrein * als Abbildung
, so dass zusammen mit den ersten beiden folgt, dass (U, + ) eine Untergruppe von (V, + ), insb. also eine abelsche Gruppe ist. Da obendrein * als Abbildung 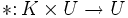 aufgefasst werden kann und sich Assoziativität, Distributivgesetze und die Neutralität der 1 direkt von V übertragen, folgt dass U mit diesen Verknüpfungen ein K-Vektorraum ist.
aufgefasst werden kann und sich Assoziativität, Distributivgesetze und die Neutralität der 1 direkt von V übertragen, folgt dass U mit diesen Verknüpfungen ein K-Vektorraum ist.Basis eines Vektorraums
- Hauptartikel: Basis
Für endlich viele
 und
und 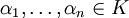 bezeichnet man die Summe
bezeichnet man die Summeals Linearkombination der Vektoren
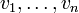 . Dabei ist s selbst wieder ein Vektor aus dem Vektorraum V.
. Dabei ist s selbst wieder ein Vektor aus dem Vektorraum V.Ist S eine Teilmenge von V, so wird die Menge aller Linearkombinationen von Vektoren aus S die lineare Hülle von S genannt. Sie ist ein Untervektorraum von V, und zwar der kleinste Untervektorraum, der S enthält.
Eine Teilmenge S eines Vektorraums V heißt linear abhängig, wenn sich der Nullvektor auf nicht-triviale Weise als eine Linearkombination von Vektoren
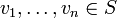 ausdrücken lässt. „Nicht-trivial“ bedeutet, dass mindestens ein Skalar (ein Koeffizient der Linearkombination) von null verschieden ist. Andernfalls heißt S linear unabhängig.
ausdrücken lässt. „Nicht-trivial“ bedeutet, dass mindestens ein Skalar (ein Koeffizient der Linearkombination) von null verschieden ist. Andernfalls heißt S linear unabhängig.Eine Teilmenge B eines Vektorraums V ist eine Basis von V, wenn B linear unabhängig ist und die lineare Hülle von B der ganze Vektorraum ist. Ein Vektorraum kann verschiedene Basen besitzen, jedoch hat jede Basis desselben Vektorraums gleich viele Elemente. Die Anzahl der Elemente einer Basis ist die Dimension des Vektorraums. Die Linearfaktoren der Darstellung eines Vektors in den Basisvektoren heißen Koordinaten des Vektors bezüglich der Basis und sind Elemente des zugrundeliegenden Körpers. Erst durch Einführung einer Basis werden jedem Vektor seine Koordinaten bezüglich der gewählten Basis zugeordnet. Dadurch wird das Rechnen in Vektorräumen erleichtert, insbesondere wenn man statt Vektoren in "abstrakten" Vektorräumen ihre zugeordneten "anschaulichen" Koordinatenvektoren verwenden kann.
Verallgemeinerungen
- Wenn man an Stelle eines Körpers K einen kommutativen Ring zugrunde legt, erhält man einen Modul. Moduln sind eine gemeinsame Verallgemeinerung der Begriffe abelsche Gruppe (für den Ring der ganzen Zahlen) und Vektorraum (für Körper).
- Einige Autoren verzichten in der Definition von Körpern auf das Kommutativgesetz der Multiplikation und nennen Moduln über Schiefkörpern ebenfalls Vektorräume. Folgt man dieser Vorgehensweise, so müssen K-Linksvektorräume und K-Rechtsvektorräume unterschieden werden, wenn der Schiefkörper nicht kommutativ ist. Die oben gegebene Definition des Vektorraums ergibt dabei einen K-Linksvektorraum, da die Skalare im Produkt auf der linken Seite stehen. K-Rechtsvektorräume werden analog mit der spiegelbildlich erklärten Skalarmultiplikation definiert.
- Wenn man an Stelle eines Körpers K einen Halbkörper zugrunde legt, erhält man einen Halbvektorraum.
- Eine andere Verallgemeinerung von Vektorräumen sind Vektorbündel; sie bestehen aus je einem Vektorraum für jeden Punkt eines Basisraumes.
Literatur
- Gerd Fischer: Lineare Algebra. Vieweg-Verlag, ISBN 3-528-03217-0.
Weblinks
- Lehrportal – Vektorraumtheorie (inkl. Übungsaufgaben)
Einzelnachweise
Wikimedia Foundation.