- Unterstreichungsalgorithmus
-
Der Markierungsalgorithmus ist ein Algorithmus zur Überprüfung von Horn-Formeln auf Erfüllbarkeit. Im Unterschied zu allgemeinen aussagenlogischen Formeln, für die vermutet wird, dass kein Polynomialzeit-Algorithmus existiert (siehe Erfüllbarkeitsproblem der Aussagenlogik), ist mit dem Markierungsalgorithmus auf der Menge der Horn-Formeln, die eine Teilmenge der aussagenlogischen Formeln darstellen, ein Polynomialzeit-Algorithmus bekannt (eine Implementierung in linearer Zeit ist möglich).
Horn-Formeln
Horn-Formeln sind eine Konjunktion von Horn-Klauseln. Horn-Klauseln sind dabei spezielle Klauseln, die höchstens ein positives Literal besitzen. Horn-Klauseln lassen sich nach den Regeln der Aussagenlogik auch als Implikation darstellen. Die folgende Tabelle gibt einen Überblick über die zwei möglichen Typen einer Horn-Klausel und ein Beispiel in Form der Disjunktion und der Implikation.
Typ Disjunktion Implikation 1 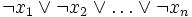

2 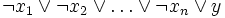

Die Variable n kann für Klauseln vom Typ 2 auch 0 sein. Horn-Formeln, die nur Klauseln vom Typ 1 enthalten, sind trivialerweise erfüllbar. Durch die Belegung der Variablen mit 0 wird die gesamte Aussage wahr. Horn-Formeln, die nur Klauseln vom Typ 2 besitzen, sind erfüllbar. Durch Belegung aller Variablen mit 1 wird dieser Sachverhalt leicht nachgewiesen.
Algorithmus
Sei φ eine beliebige Horn-Formel. Folgender Algorithmus erkennt, ob φ erfüllbar ist, oder nicht.
- Für alle Klauseln der Form ψ = x1:
- Markiere x1
- Solange φ Klauseln
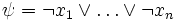 vom Typ 1 oder
vom Typ 1 oder  vom Typ 2 enthält, so dass
vom Typ 2 enthält, so dass 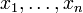 markiert sind und y im Falle von Klauseln von Typ 2 noch nicht markiert ist:
markiert sind und y im Falle von Klauseln von Typ 2 noch nicht markiert ist:
- Falls φ eine entsprechende Klausel ψ vom Typ 1 enthält:
- Beende den Algorithmus mit der Ausgabe unerfüllbar.
- Andernfalls:
- Wähle eine entsprechende Klausel ψ vom Typ 2 beliebig und
- markiere y überall in φ.
- Falls φ eine entsprechende Klausel ψ vom Typ 1 enthält:
- Beende den Algorithmus mit der Ausgabe erfüllbar. Wenn man alle markierten Variablen mit wahr belegt und die restlichen Variablen mit falsch, so erhält man eine Belegung, die φ erfüllt.
Motivation des Algorithmus: Der Algorithmus markiert alle Variablen die zwangsläufigerweise mit wahr belegt werden müssen (nämlich zuerst die Variablen in den Klauseln die nur aus einem positiven Literal bestehen, und danach in den Klauseln die eine Implikation darstellen und bei denen die Variablen auf der linken Seite der Implikation schon alle mit wahr belegt sind die Variable auf der rechten Seite.). Wenn sich dabei kein Widerspruch ergibt ist die Formel erfüllbar.
Weblinks
- Für alle Klauseln der Form ψ = x1:
Wikimedia Foundation.
