- Verzerrungsblindleistung
-
Die Verzerrungsblindleistung ist ein Begriff aus der Elektrotechnik/Elektronik und beschreibt eine spezielle Form der Blindleistung, die in Wechsel- bzw. Drehstromnetzen durch nichtlineare Verbraucher verursacht wird. Die Bezeichnung wird in der Literatur nicht einheitlich gewählt. Alternative Bezeichnungen sind Verzerrungsleistung, Oberschwingungsblindleistung oder Oberwellenblindleistung.
Inhaltsverzeichnis
Allgemeines
Stromversorgungsnetze werden praktisch fast immer mit sinusförmiger Wechselspannung betrieben. Daher hat bei linearen elektrischen Bauelementen wie elektrischen Widerständen oder sogenannten Blindwiderständen der Strom ebenfalls einen sinusförmigem Verlauf. Sind Strom und Spannung sinusförmig tritt keine Verzerrungsblindleistung auf. Verzerrungsblindleistung tritt immer dann auf, wenn ein nichtsinusförmiger Strom und/oder eine nichtsinusförmige Spannung vorhanden sind. Bei elektrischen Verbrauchern, die Verzerrungsblindleistung erzeugen, kann meistens von einer sinusförmigen Spannung (wird durch das Versorgungsnetz bereitgestellt) und einem verzerrten bzw. oberschwingungsbehafteten Strom ausgegangen werden.
Die Ursache für den nichtsinusförmigen Strom und die Verzerrungsblindleistung sind nichtlineare elektrische Baugruppen, wie Gleichrichter in Netzteilen, Wechselrichter oder auch magnetische Bauteile, die magnetische Sättigungserscheinungen zeigen. Diese Baugruppen verursachen in den Leitungen verzerrte und nichtsinusförmige Wechselströme. Dieser nichtsinusförmige Stromverlauf kann durch eine Fourieranalyse als eine Summe von sogenannten Oberschwingungen dargestellt werden. Diese Oberschwingungen des Stromes in Kombination mit der sinusförmigen Netzspannung ergeben Blindleistungsanteile, die als Verzerrungsblindleistung bezeichnet werden. Die Grundschwingung des Stromes ergibt mit der Spannung die Grundschwingungssscheinleistung, die wiederum in Wirkleistung und Grundschwingungsblindleistung aufgeteilt werden kann.
Der Begriff rührt daher, dass nichtlineare elektrische Bauteile den sinusförmigen zeitlichen Verlauf des Stromes verzerren/verschleifen. Die dabei auftretenden Oberschwingungen sind dabei fast immer unerwünscht, da Sie genau wie die grundschwingungsscheinleistung das Netz belasten und am Verbraucher keine Arbeit verrichten können. Ebenfalls sind sie auch oft die Ursache von elektromagnetischen Störungen sein. Durch den Einsatz von Leistungsfaktorkorrekturfilter kann der Anteil an Oberschwingungen reduziert werden.
Berechnung
Die Wirkleistung P ist die Leistung, die an einem Verbraucher in der Lage ist, Arbeit zu verrichten, beispielsweise eine Drehbewegung gegen ein drehmoment beim Elektromotors oder die Temperatursteigerung einer Elektroheizung. Wirkleistung in oberschwingungsbehafteten Systemen können nur Harmonische von Strom und Spannung erzeugen, welche die gleiche Ordnungszahl haben. Da die Spannung in der Regel ja keine Oberschwingungsanteile besitzt, generiert also nur die Grundschwingung des Stromes mit der (Grundschwingung der) Spannung Wirkleistung und gegebenenfalls Grundschwingungsblindleistung. Wird von einer sinusförmigen Spannung ausgegangen, so ergeben die Produkte der Spannungsgrundschwingung mit den Oberschwingungen des Stromes Verzerrungsblindleistung. Die Grundschwingungs-Blindleistung
 ist eine Leistungskomponente, die infolge der Energiespeicherung in den induktiven oder kapazitiven Anteilen der Verbraucher periodisch zwischen Erzeuger (Kraftwerk) und Verbraucher hin- und herpendelt und an sich unerwünscht ist, da sie Leitungen zusätzlich belastet. Die Grundschwingungs-Scheinleistung
ist eine Leistungskomponente, die infolge der Energiespeicherung in den induktiven oder kapazitiven Anteilen der Verbraucher periodisch zwischen Erzeuger (Kraftwerk) und Verbraucher hin- und herpendelt und an sich unerwünscht ist, da sie Leitungen zusätzlich belastet. Die Grundschwingungs-Scheinleistung  ist die vektorielle Summe aus Wirkleistung und Grundschwingungsblindleistung:
ist die vektorielle Summe aus Wirkleistung und Grundschwingungsblindleistung:Bei oberschwingungsbehafteten Größen kommt nunmehr eine dritte Komponente, die Verzerrungsblindleistung D hinzu, welche die Blindleistung in den Oberschwingungen darstellt. Ist
 der Effektivwert des Grundschwingungsstromes,
der Effektivwert des Grundschwingungsstromes,  der Gleichstromanteil des Stromes und
der Gleichstromanteil des Stromes und  ,
,  usw. die Effektivwerte der Oberschwingungsströme, U der Effektivwert der Spannung, so lässt sich der Verzerrungsblindstrom als
usw. die Effektivwerte der Oberschwingungsströme, U der Effektivwert der Spannung, so lässt sich der Verzerrungsblindstrom alsausdrücken und die Verzerrungsblindleistung als
Die gesamte Blindleistung, in nebenstehender Abbildung nicht explizit dargestellt, ergibt sich aus der Grundschwingungsblindleistung und der Verzerrungsblindleistung zu
Der gesamte Betrag der Scheinleistung S ist im allgemeinen Fall nach DIN 40 110 ff gegeben durch:[1]
In nebenstehender Abbildung ist das Zeigerdiagramm mit den Zeigern für die verschiedenen Leistungen dargestellt.
Zusammenhang mit dem Klirrfaktor
Der Klirrfaktor k einer oberschwingungsbehafteten Größe
 - oftmals auch Oberschwingungsgehalt genannt - ist ein Maß für die qualitative Bewertung der Verzerrung und die Größe der Verzerrungsblindleistung in elektrischen Systemen. Der Klirrfaktor beschreibt das Verhältnis der geometrischen Summe der Effektivwerte
- oftmals auch Oberschwingungsgehalt genannt - ist ein Maß für die qualitative Bewertung der Verzerrung und die Größe der Verzerrungsblindleistung in elektrischen Systemen. Der Klirrfaktor beschreibt das Verhältnis der geometrischen Summe der Effektivwerte  des Oberschwingungsspektrums zur geometrischen Summe der Effektivwerte des Gesamtspektrum
des Oberschwingungsspektrums zur geometrischen Summe der Effektivwerte des Gesamtspektrum  inklusive des Grundschwingsanteils
inklusive des Grundschwingsanteils  . Die Verzerrungsblindleistung lässt sich auch mit dem Klirrfaktor k und der Scheinleistung S ausdrücken:
. Die Verzerrungsblindleistung lässt sich auch mit dem Klirrfaktor k und der Scheinleistung S ausdrücken:Die zum Oberschwingungsgehalt antivalente Größe ist der Grundschwingungsgehalt g. Dieser beschreibt das Verhältnis des Effiktivwertes
 der Grundschwingung einer oberschwingungsbehafteten Größe
der Grundschwingung einer oberschwingungsbehafteten Größe  zur geometrischen Summe der Effektivwerte
zur geometrischen Summe der Effektivwerte  des gesamten Frequenzspektrums dieser Größe.
des gesamten Frequenzspektrums dieser Größe.Beispiele
- Bei idealen, linearen Blindwiderständen wie Kondensatoren oder Induktivitäten tritt keine Verzerrungsblindleistung D auf, sondern ausschließlich die Grundschwingungsblindleistung
 .
. - Bei einem mit einer Diode in Serie geschalteten ohmschen Lastwiderstand R, z. B. einer Glühlampe, tritt an einer sinusförmigen Wechselspannungsquelle mit der Effektivspannung U zwar keine Blindleistung
 in der Grundschwingung auf, da der Energiespeicher fehlt, sondern nur eine Wirkleistung P und Verzerrungsblindleistung D infolge der Oberschwingungen. Bemerkenswert dabei ist, dass in dieser Schaltung, in der die Glühlampe R mit dem Einweggleichrichter betrieben wird, die Wirkleistung P betragsmäßig gleich groß wie die Verzerrungsblindleistung D ist und den Betrag
in der Grundschwingung auf, da der Energiespeicher fehlt, sondern nur eine Wirkleistung P und Verzerrungsblindleistung D infolge der Oberschwingungen. Bemerkenswert dabei ist, dass in dieser Schaltung, in der die Glühlampe R mit dem Einweggleichrichter betrieben wird, die Wirkleistung P betragsmäßig gleich groß wie die Verzerrungsblindleistung D ist und den Betrag
- aufweist. Da diese Einweggleichrichtung dem Laststrom einen Gleichstromanteil aufprägt, ist bei größeren Leistungen diese Form des einfachen Dimmens von Glühlampen durch Vorschalten einer Diode nicht mehr zulässig. Der vorgeschaltete Ortsnetztransformator könnte ansonsten vormagnetisiert werden und damit im ungünstigsten Fall in die Sättigung geraten.
Oberschwingungsanteile bei verschiedenen Verbrauchern
In folgender Tabelle sind verschiedene Verbraucher und deren Oberschwingungsverteilung ohne Filterung bei Betrieb an sinusförmiger Wechselspannung aufgelistet. Die Oberschwingungsströme sind relativ zur Grundschwigung des Stromes angegeben. Dabei gilt allgemein: Je höher die Oberschwingungsanteile im Strom desto höher die Verzerrungsblindleistung der betreffenden Verbraucher.[2]
Ursache von Oberschwingungsströmen und der Verzerrungsblindleistung Ursache Kennlinie Verbraucher In/I1 [%] n=2 n=3 n=4 n=5 n=7 – 
Glühlampe,
Kondensator0 0 0 0 0 magnetische Sättigung 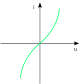
Transformator mit
unterdimensionierten Kern0 25…55 0 8…30 2…10 Gasentladung,
Glimmentladung
Leuchtstofflampe 1…2 8…20 0 2…3 1…2 Einweggleichichter
mit ohmscher Last
ohne Glättungskondensator
Leistungshalbierung thermischer
Geräte wie Haarfön42 0 8 0 0 Einweggleichichter
mit kapazitiver und ohmscher Last,
mit Glättungskondensator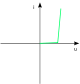
Einfache Kleinstnetzteile
Unterhaltungselektronik70…90 40…60 30…50 25…50 12…25 Vollweggleichichter
mit kapazitiver und ohmscher Last,
mit Glättungskondensator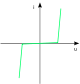
Netzteile in PCs, Druckern,
Monitor, TV0 65…80 0 50…70 25…35 Auswirkungen
Besonders im Konsumgüterbereich ist es in den letzten Jahren zu einem Anwachsen von Verbrauchern gekommen, die netzseitig einen Gleichrichter haben und somit Verzerrungsblindlesitung erzeugen. Dazu gehören z.B. Energiesparlampen und Netzteile für Computer, Monitore, TV-Geräte usw. Aus diesem Grund ist bei Verbrauchern mit einer Leistung über 75 W ein Leistungsfaktorkorrekturfilter (PFC), üblicherweise als sogenannter aktiver Leistungsfaktorkorrekturfilter ausgeführt, vorzusehen.[3]
Da die Verzerrungsblindleistung vom Netz übertragen werden muss, kommt es zu einer stärkeren Beanspruchung des elektrischen Versorgungsnetzes und Störungen wie Flicker. Im Gegensatz zu den Strömen der Grundschwingung heben sich die Ströme der durch drei teilbaren Oberschwingungen im Neutralleiter eines Dreiphasenwechselstromnetzes nicht auf, sondern addieren sich. Dies betrifft bei der in Europa üblichen Netzfrequenz von 50 Hz insbesondere die dritte Harmonische mit 150 Hz und die neunte Harmonische mit 450 Hz. Dadurch kann es, insbesondere wenn der Neutralleiter mit deutlich geringeren Querschnitt als die Außenleiter ausgeführt ist, zu einer unzulässig hohen Strombelastung am Neutralleiter kommen.
Die Grenzwerte der Oberschwingungsanteile in Prozent relativ zur Nennspannung in öffentlichen Niederspannungsnetzen (230 V zwischen Außenleiter und Neutralleiter) und im Mittelspannungsnetz (zwischen zwei beliebigen Außenleitern mit 10 kV bzw. 20 kV) sind festgelegt zu:
Grenzwerte gemäß DIN EN 50160 Ungerade Harmonische Gerade Harmonische Nichtvielfache von 3 Vielfache von 3 Ordnung %UNenn Ordnung %UNenn Ordnung %UNenn 5 6,0% 3 5,0 % 2 2,0 % 7 5,0% 9 1,5 % 4 1,0 % 11 3,5% 15 0,5 % 6 ≤ n ≤ 24 0,5 % 13 3,0% 21 0,5 % 17 2,0% 19 1,5% 23 1,5% 25 1,5% Literatur
- Flosdorff, Hilgarth: Elektrische Energieverteilung, Teubner Verlag, 2003, ISBN 3-519-26424-2
- Budeanu, Constantin: Puissances reactives et fictives 1927
Einzelnachweise
- ↑ Ruhr-Universität Bochum, Lehrstuhl für elektrische Energietechnik und Leistungselektronik: Grundlagen der Energietechnik., 25. August 2004, S. 55.
- ↑ R. Gretsch: Oberschwingungen in Stromversorgungsnetzen; Lehrgangsunterlagen „Spannungsqualität“ an der Technischen Akademie Esslingen, 2001
- ↑ DIN EN 61000-3-2, Elektromagnetische Verträglichkeit (EMV) - Teil 3-2: Grenzwerte für Oberschwingungsströme (Geräte-Eingangsstrom < 16 A je Leiter), Deutsche Fassung EN 61000-3- 2: 2000
Wikimedia Foundation.










