- Viereck
-
Ein Viereck (veraltet auch Geviert, auch Tetragon) ist eine Figur der ebenen Geometrie, nämlich ein Vieleck mit vier Ecken und vier Seiten. In der Mathematik definiert man (ebene) Vierecke als Polygone mit vier Ecken, und (daher auch) vier Kanten (oder Seiten). Analog zu Dreiecken ist auch eine Verallgemeinerung des Vierecksbegriffes auf nichteuklidische Geometrien (gekrümmte Vierecke) möglich. In der projektiven Geometrie spielen vollständige Vierecke und die dazu dualen vollständigen Vierseite eine wichtige Rolle.
Das regelmäßige (oder reguläre) Viereck ist das Quadrat.
Ein Viereck hat zwei Diagonalen. Liegen beide Diagonalen innerhalb des Vierecks, so ist das Viereck konvex (konvexes Viereck), liegt genau eine Diagonale außerhalb, so hat das Viereck eine konkave Ecke (nicht-konvexes Viereck). Bei einem überschlagenen (auch: verschränkten) Viereck liegen beide Diagonalen außerhalb des Vierecks (als Beispiel siehe verschränktes Trapez). Überschlagene Vierecke sind verallgemeinerte Polygone und werden normalerweise nicht zu den (normalen oder "echten") Vierecken gerechnet. Gleiches gilt für entartete Vierecke, bei denen zwei oder mehr Eckpunkte zusammenfallen oder mehr als zwei Eckpunkte auf einer Geraden liegen.
- Die Summe der Innenwinkel in einem Viereck beträgt 360 Grad bzw. 2π.
Inhaltsverzeichnis
Spezielle Vierecke
Ein Trapez ist ein Viereck mit mindestens zwei parallelen Seiten. Sind je zwei einander gegenüberliegende Seiten parallel, spricht man vom Parallelogramm. Ein Viereck, welches vier gleich große (Innen-)Winkel (90°, siehe rechter Winkel) hat, ist ein Rechteck. Beim Drachenviereck (Deltoid) stehen die Diagonalen senkrecht aufeinander, und eine Diagonale wird durch die andere halbiert. Dies ist gleichbedeutend damit, dass es zwei Paare benachbarter Seiten gibt, die jeweils gleich lang sind. Bei vier gleich langen Seiten spricht man von einem Rhombus (Raute). Ein Quadrat hat vier gleich lange Seiten und auch vier gleich große (Innen-)Winkel (90°). Bei einem Sehnenviereck sind die vier Seiten Sehnen des Umkreises. Sind die vier Seiten Tangenten eines Inkreises, so spricht man von einem Tangentenviereck.
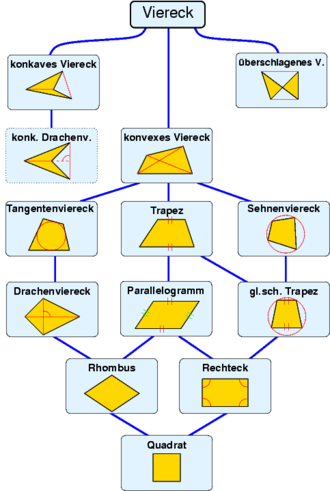
Zwischen den einzelnen Vierecktypen gelten diverse Mengenrelationen, insb. die in der Grafik dargestellten Teilmengenbeziehungen, wie zum Beispiel:
- Quadrat ⊂ Rechteck ⊂ Parallelogramm ⊂ Trapez ⊂ konvexes Viereck
(Dabei steht jeweils der Begriff X synonym für Menge aller X)
Ferner gelten auch noch folgende Beziehungen:
- Quadrat = Rechteck ∩ Raute
- Quadrat = Drachenviereck ∩ gleichschenkliges Trapez
- Rechteck = Sehnenviereck ∩ Parallelogramm
- Raute = Drachenviereck ∩ Trapez
- Raute = Tangentenviereck ∩ Parallelogramm
- Gleichschenkliges Trapez = Sehnenviereck ∩ Trapez
Klassifikation
Die ebenen Vierecke werden nach verschiedenen Gesichtspunkten eingeteilt:
- nach Eigenschaften des Inneren:
- konvex
- nicht konvex
- nach Symmetrie-Eigenschaften:
- eine Diagonale ist Symmetrieachse: Deltoid
- beide Diagonalen sind Symmetrieachsen: Rhombus
- die Mittelsenkrechte einer Seite ist eine Symmetrieachse: gleichschenkeliges Trapez
- die Mittelsenkrechten zweier Seiten sind Symmetrieachsen: Rechteck
- vier Symmetrieachsen: Quadrat
- zweizählige Symmetrie (punktsymmetrisch): Parallelogramm
- vierzählige Symmetrie: Quadrat
- nach der Länge der Seiten:
- zwei Paare gleich langer gegenüberliegender Seiten: Parallelogramm
- zwei Paare gleich langer benachbarter Seiten: Deltoid (Drachenviereck)
- gleichseitiges Viereck: Rhombus
- die Summe der Längen gegenüberliegender Seiten ist gleich: Tangentenviereck
- nach der Größe der Winkel:
- zwei Paare gleich großer gegenüberliegender Winkel: Parallelogramm
- zwei Paare gleich großer benachbarter Winkel: gleichschenkeliges Trapez
- gleichwinkeliges Viereck: Rechteck
- die Summe gegenüberliegender Winkel ergibt 180°: Sehnenviereck
- nach der Lage der Seiten:
- ein Paar paralleler Seiten: Trapez
- zwei Paar paralleler Seiten: Parallelogramm
- die Seiten berühren denselben Kreis (den Inkreis): Tangentenviereck
- nach der Lage der Ecken:
- die Ecken liegen auf einem Kreis (dem Umkreis): Sehnenviereck
Formeln
Die Vierecksfläche A lässt sich ermitteln aus
Sind die Koordinaten der Eckpunkte gegeben, so erhält man mit der gaußschen Trapezformel den einfachen Ausdruck
 .
.
Ein Viereck kann unter anderem durch geeignete Kombinationen folgender Angaben (fünf voneinander unabhängige Bestimmungsstücke) beschrieben werden:
- Winkel an den Ecken (Innenwinkel)
- Länge der Seiten
- Länge der Diagonalen
- Umfang
- Fläche
Manche Kombinationen, z.B. "4 Seiten und 1 Innenwinkel" sind jedoch mehrdeutig, da die dem gegebenen Winkel gegenüberliegende Ecke konvex oder konkav sein kann.
Schwerpunkt
Bei punktsymmetrischen Vierecken (Parallelogrammen) ist der Schwerpunkt das Symmetriezentrum, also der Diagonalenschnittpunkt.
Im Allgemeinen muss man unterscheiden zwischen dem Eckenschwerpunkt (alle Masse sitzt in den Ecken, jede Ecke hat die gleiche Masse) und dem Flächenschwerpunkt (die Masse ist gleichmäßig über die Fläche des Vierecks verteilt.) Beim Dreieck stimmen diese beiden Schwerpunkt überein. Daneben gibt es noch den Kantenschwerpunkt (die Masse ist gleichmäßig auf die Kanten verteilt, die Masse jeder Kante ist proportional zu ihrer Länge). Der Kantenschwerpunkt wird jedoch selten betrachtet. Er stimmt auch beim Dreieck nicht mit dem Flächen- und Eckenschwerpunkt überein, sondern entspricht dort dem Inkreismittelpunkt des Mittendreiecks.[1]
Den Flächenschwerpunkt eines Vierecks kann man wie folgt konstruieren: Man zerlegt das Viereck durch eine Diagonale in zwei Dreiecke und bestimmt jeweils deren Schwerpunkt als Schnittpunkt der Seitenhalbierenden . Diese beiden Punkte verbindet man durch eine Gerade. Dasselbe wiederholt man, indem man das Viereck durch die andere Diagonale teilt. Der Schnittpunkt der beiden Verbindungsgeraden ist der Schwerpunkt des Vierecks.[1]
Begründung: Die Gerade durch die beiden Dreiecksschwerpunkte ist eine Schwerlinie beider Dreiecke und damit auch des Vierecks. Also muss der Schwerpunkt auf dieser Geraden liegen.
Den Eckenschwerpunkt erhält man, indem man die Mittelpunkte gegenüberliegender Seiten verbindet. Der Schnittpunkt der beiden Verbindungslinien ist der Eckenschwerpunkt.[1] Ist ein kartesisches Koordinatensystem gegeben, so kann man die Koordinaten des Eckenschwerpunkts S(xS | yS) aus den Koordinaten der Ecken A(xA | yA),B(xB | yB),C(xC | yC),D(xD | yD) berechnen:
Einzelnachweise
- ↑ a b c Hartmut Wellstein: Elementargeometrie, Vorlesungsskript, Website der Universität Flensburg 2000/2001, Kapitel 1 Schwerpunkte, abgerufen am 13. Februar 2011
Siehe auch
- Ungleichungen in Vierecken
- Zu den Begriffen vollständiges Viereck und vollständiges Vierseit in der projektiven Geometrie siehe deren Definition im Artikel Fano-Axiom
Weblink
-
 Wiktionary: Viereck – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen
Wiktionary: Viereck – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen
Kategorien:- Vierecksgeometrie
- Geometrische Figur
Wikimedia Foundation.