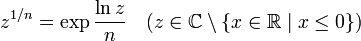- Wurzelgesetz
-
 Grafische Darstellung der Quadratwurzel-Funktion
Grafische Darstellung der Quadratwurzel-Funktion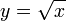
In der Mathematik versteht man unter Wurzelziehen oder Radizieren die Bestimmung der Unbekannten x in der Potenz
wobei zunächst a eine nichtnegative reelle Zahl und n>1 eine natürliche Zahl sein soll. Das Ergebnis des Wurzelziehens bezeichnet man als Wurzel oder Radix (von lat. Radix „Wurzel“). Das Radizieren ist die Umkehrung des Potenzierens.
Inhaltsverzeichnis
Schreibweise und Bezeichnungen
Man schreibt die nichtnegative Lösung der Gleichung a = xn in der Form
und liest: x ist die n-te Wurzel aus a. Man nennt
- x Wurzel oder Radix,
- n Wurzelexponent,
- a Radikand/Wurzelbasis.
Quadrat- und Kubikwurzel
Üblicherweise wird die zweite Wurzel als Quadratwurzel oder einfach nur als die Wurzel bezeichnet und der Wurzelexponent weggelassen. Die einfachen Quadratwurzeln, die natürliche Zahlen von 1–20 sind (kleines und großes Einmaleins), werden manchmal als höheres Allgemeinwissen betrachtet und in sogenannten Eignungstests für Personalauswahlverfahren unter Stress kurz abgefragt (z. B.: Was ist die Wurzel aus 121?).
Quadratzahlen und deren Quadratwurzeln Radikand Radix Quadratwurzel Radikand Radix Quadratwurzel 1 1 121 11 4 2 144 12 9 3 169 13 16 4 196 14 25 5 225 15 36 6 256 16 49 7 289 17 64 8 324 18 81 9 361 19 100 10 400 20 Des weiteren bezeichnet man Wurzeln mit dem Wurzelexponenten 3 (dritte Wurzeln) speziell als Kubikwurzeln.
Beispiel:
(Sprich: Dritte Wurzel aus 8 ... oder Kubikwurzel aus 8 ...)
Das Zeichen
Das Operatorsymbol
![\sqrt[]{\;\;}](/pictures/dewiki/51/3916a09c0d143d8ae497353c5145c942.png) stammt von dem kleinen Buchstaben r ab und steht für radizieren. Er wurde erstmalig 1525 vom deutschen Mathematiker Christoph Rudolff verwendet. Die Verlängerung des r über den vollständigen Term wurde erst später eingeführt.
stammt von dem kleinen Buchstaben r ab und steht für radizieren. Er wurde erstmalig 1525 vom deutschen Mathematiker Christoph Rudolff verwendet. Die Verlängerung des r über den vollständigen Term wurde erst später eingeführt.Traditionen des Formelsatzes
Die verschiedenen Formelsatztraditionen lassen den oben genannten Ursprung mehr oder weniger deutlich zutage treten. Die Form des Wurzelzeichens im amerikanischen Formelsatz zeigt nur wenig Ähnlichkeit mit dem kleinen r. Besonders der schräge Abwärtstrich an der linken Seite des Zeichens unterscheidet es von der Form in anderen Traditionen des Formelsatzes. Das Wurzelzeichen zeigt, abhängig von seiner Größe, leicht unterschiedliche Varianten, wie in der folgenden Formel zu sehen ist:
![\sqrt{\sqrt[n]{\sqrt[3]{3}}}](/pictures/dewiki/101/e3589071e8768b8106b36cb4db60b984.png) .
.
Das Wurzelzeichen im deutschen und russischen Formelsatz hingegen zeigt größenunabhängig immer dieselbe Form. Die deutsche Form des Wurzelzeichens ähnelt sehr stark dem Kleinbuchstaben r. Der linke Anstrich hat jedoch nicht notwendigerweise dieselbe Höhe wie der Strich über dem Radikanden, wie im Bild Deutsche Form des Wurzelzeichens dargestellt, so dass der Übergang zur russischen Form fließend ist.
Das Wurzelzeichen im russischen Formelsatz zeigt eine Form, die sowohl Eigenschaften der deutschen wie der amerikanischen Form hat.
Auch sind Wurzelzeichen im amerikanischen Satz in Textformeln immer kleiner als in abgesetzten Formeln, um störende Zeilenabstände einzuschränken.
Webtypographische Darstellung
Probleme mit diesem speziellen Zeichen ergeben sich bei der elektronischen Darstellung, es lässt sich in der Regel nicht direkt über die Tastatur eingeben. Neben der Darstellung mittels spezieller Software (z. B. LaTeX) gibt es die Möglichkeit, mit Unicode bzw. per HTML das Zeichen als „√“ – √ – (gleichbedeutend: „√“) darzustellen. Hier ergibt sich aber das Problem, dass der Radikand nicht „unter“ der Wurzel steht, weil der Letternsatz kein sinnvolles Weiterziehen des Wurzelzeichens erlaubt.
Mathematische Grundlagen
Zusammenhang mit Potenzen
Das Radizieren mit dem Wurzelexponenten n und das Potenzieren mit dem Exponenten n heben sich gegenseitig auf, es gilt gemäß obenstehender Definition der Wurzel:
Das Radizieren mit dem Wurzelexponenten n wirkt also wie das Potenzieren mit dem Exponenten
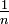 . Nach den Rechenregeln für Potenzen gilt nämlich:
. Nach den Rechenregeln für Potenzen gilt nämlich:Daher kann das Radizieren mit dem Wurzelexponenten n auch als Potenzieren mit dem Exponenten 1/n interpretiert werden:
Eindeutigkeit von Wurzeln aus positiven Zahlen
Obwohl die eingangs genannte Fragestellung bei geradzahligen Wurzelexponenten und positiven Radikanden zwei Lösungen mit unterschiedlichen Vorzeichen besitzt, steht die Schreibweise mit dem Wurzelzeichen
![\sqrt[]{}](/pictures/dewiki/57/9fbe06280543646a9247b7dd015f1401.png) grundsätzlich für die positive Lösung. Beispielsweise hat die Gleichung x2 = 4 die beiden Lösungen 2 und −2. Der Term
grundsätzlich für die positive Lösung. Beispielsweise hat die Gleichung x2 = 4 die beiden Lösungen 2 und −2. Der Term ![\sqrt[2]{4}](/pictures/dewiki/97/a4290e26cf940a660daa719648d4e57d.png) hat jedoch den Wert 2 und nicht den Wert −2. Allgemein gilt daher für geradzahlige Wurzelexponenten
hat jedoch den Wert 2 und nicht den Wert −2. Allgemein gilt daher für geradzahlige WurzelexponentenWurzeln aus negativen Zahlen
Die Behandlung von Wurzeln aus negativen Zahlen ist nicht einheitlich. Es gilt beispielsweise
und − 2 ist die einzige reelle Zahl, deren dritte Potenz − 8 ist. Allgemein ergeben sich für ungerade Potenzen negativer Zahlen wieder negative Zahlen.
Bezüglich der ungeraden Wurzeln aus negativen Zahlen werden folgende Positionen vertreten:
- Wurzeln aus negativen Zahlen sind generell „verboten“. Beispielsweise ist
![\sqrt[3]{-8}](/pictures/dewiki/101/e6ca3a3950c92e57c2faf7983423235a.png) also undefiniert. Die Lösung der Gleichung x3 = − 8 wird geschrieben als
also undefiniert. Die Lösung der Gleichung x3 = − 8 wird geschrieben als ![x = -\sqrt[3]{8}](/pictures/dewiki/48/046bdeceaf4b9a6e222e0a7c0c151370.png) .
. - Wurzeln aus negativen Zahlen sind erlaubt, wenn der Wurzelexponent eine ungerade Zahl ist (3, 5, 7, …). Für ungerade Zahlen 2n + 1 gilt generell
-
![\sqrt[2n+1]{-a}=-\sqrt[2n+1]{a}](/pictures/dewiki/102/f65b59ef82e4c09f447ffd24084aa39f.png) .
.
- Diese Festlegung ist mit manchen Eigenschaften der Wurzeln, die für positive Radikanden gelten, nicht vereinbar. Beispielsweise ist
Wurzeln zu geraden Exponenten aus negativen Zahlen können keine reellen Zahlen sein, weil gerade Potenzen reeller Zahlen nie negativ sind. Der Bedarf für Wurzeln aus negativen Zahlen führte zur Einführung der komplexen Zahlen; allerdings gibt es auch im Bereich der komplexen Zahlen Wurzeln aus negativen Zahlen nur mit gewissen Einschränkungen, siehe unten.
Die Wurzelgesetze
Die Rechenregeln für Wurzeln ergeben sich aus jenen für Potenzen.
Für positive Zahlen a und b gelten die folgenden Rechengesetze:
Bei negativen Zahlen können diese Rechengesetze nur angewendet werden, wenn m und n ungerade Zahlen sind. Bei komplexen Zahlen sind sie gänzlich zu vermeiden.
Es gelten außerdem die Konvergenzen
![\lim_{n\rightarrow\infty}\sqrt[n]{n}= 1](/pictures/dewiki/57/903c5708320bb33d547a61fbde6df582.png) ,
,
- wie man mit Hilfe des binomischen Lehrsatzes und der Ungleichung
![\left(1 + \sqrt[2]{\tfrac{2}{n}}\right)^n > n](/pictures/dewiki/50/24b8c578e2e9855c233c17a910c741a5.png)
- zeigen kann.
![\lim_{n\to\infty}\sqrt[n]{n^k} = 1](/pictures/dewiki/57/9cb350bdcb0caaa8583f512f531e966e.png) , wobei k eine beliebige, aber feste natürliche Zahl darstellt.
, wobei k eine beliebige, aber feste natürliche Zahl darstellt.
 ,
,
- wie aus der Exponentialdarstellung von
![\sqrt[n]{n}](/pictures/dewiki/97/a527e22f03e9a4fa5e5a267ae77eede5.png) hervorgeht.
hervorgeht.
Wurzelfunktionen
Funktionen der Form
![f: \mathbb{R}_0^+\to\mathbb{R}_0^+, x\mapsto\sqrt[n]x](/pictures/dewiki/98/be6c7b46490472d330d572b8b4dc548c.png) oder allgemeiner
oder allgemeiner ![x\mapsto\sqrt[n]{x^m}](/pictures/dewiki/48/04f14d2a38265816791fa82c784a3879.png)
heißen Wurzelfunktionen. Sie sind Potenzfunktionen, es gilt
![\sqrt[n]{x^m}=x^\frac{m}{n}](/pictures/dewiki/97/a5f5696f141b793e077aafe2383f0499.png) .
.Berechnung
Wurzeln können durch schriftliches Wurzelziehen bestimmt werden; dieses Verfahren ist jedoch von geringer praktischer Bedeutung.
Rückführung auf andere Funktionen
Höhere Wurzeln aus positiven Zahlen x kann man wie jede Potenz durch Exponentialfunktion und Logarithmus ausdrücken:
Numerische Berechnung
Um einen Näherungswert für eine Wurzel zu erhalten, kann man mehrere Verfahren anwenden. Dazu gehören unter anderem das Intervallhalbierungsverfahren.
Ein weiteres Näherungsverfahren zur Berechnung von
![\sqrt[n]{x}](/pictures/dewiki/53/5e4352778f3b156f05ef056f9793ec36.png) ergibt sich, indem man mit dem Newton-Verfahren eine Nullstelle der Funktion
ergibt sich, indem man mit dem Newton-Verfahren eine Nullstelle der Funktion annähert:
annähert:
- Wähle einen (möglichst guten) Startwert y > 0
- Iteriere nach der Vorschrift
Für n = 2 erhält man gerade das Heron-Verfahren.
Beispiel für eine Näherung für
![\sqrt[3]{2}](/pictures/dewiki/54/62f6a0ce6cf44d89c6f3b211c98c43bd.png) nach dem obigen Iterationsverfahren:
nach dem obigen Iterationsverfahren:Die Iterationsvorschrift lautet mit x = 2 und n = 3
 .
.
Mit dem Startwert y = 2 erhält man:
Startwert: 2,000000000000 Schritt 1: 1,500000000000 Schritt 2: 1,296296296296 Schritt 3: 1,260932224741 Schritt 4: 1,259921860565 Schritt 5: 1,259921049895 Schritt 6: 1,259921049894 Methode der „Rechenkünstler“
Man kann, wie das Rechenkünstler machen, eine Wurzel auch durch Abschätzung und Anwendung elementarer Zahlentheorie berechnen, sofern bekannt ist, dass die Wurzel eine natürliche Zahl ist. Das lässt sich besonders gut am Beispiel der dritten Wurzel zeigen. Dazu muss man zwei Dinge wissen, nämlich die Größenordnung der Kubikzahlen, und wie die letzte Ziffer endet:
1 1 8 2 27 3 64 4 125 5 216 6 343 7 512 8 729 9 1.000 10 1.000 10 8.000 20 27.000 30 64.000 40 125.000 50 216.000 60 343.000 70 512.000 80 729.000 90 1.000.000 100 Beispiele:
- Die dritte Wurzel von 103.823:
Die Zahl liegt zwischen 64.000 und 125.000, deshalb muss die Zehnerstelle der dritten Wurzel 4 sein. Die letzte Ziffer der Zahl ist eine 3, demnach ist die dritte Wurzel von 103.823 abgeschätzt 47. - Die dritte Wurzel von 12.167:
Die Zahl liegt zwischen 8.000 und 27.000, deshalb muss die Zehnerstelle der dritten Wurzel 2 sein. Die letzte Ziffer der Zahl ist eine 7, demnach ist die dritte Wurzel von 12.167 abgeschätzt 23.
Das Ganze funktioniert aber nur dann, wenn man davon ausgehen kann, dass es sich bei der vorgegebenen Zahl um die dritte Potenz einer natürlichen Zahl handelt.
Bei den Rechenkünstlern handelt es sich natürlich um viel höhere Potenzen mehrstelliger Zahlen – zum Beispiel die Berechnung der 25. Wurzel aus 880.794.982.218.444.893.023.439.794.626.120.190.780.624.990.275.329.063.400.179.824.681.489.784.873.773.249 (Lösung: 1729) und extremere Aufgaben.
Wurzeln aus komplexen Zahlen
Als die n-ten Wurzeln einer komplexen Zahl
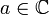 bezeichnet man die Lösungen der Gleichung
bezeichnet man die Lösungen der Gleichung- zn = a.
Ist
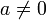 in der Exponentialform
in der Exponentialform 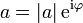 dargestellt, so sind die n-ten Wurzeln aus a genau die n komplexen Zahlen
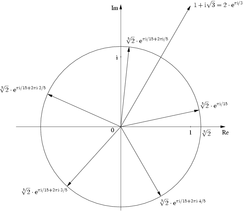
dargestellt, so sind die n-ten Wurzeln aus a genau die n komplexen ZahlenDer Sonderfall a = 1 wird als n-te Kreisteilungsgleichung bezeichnet, die Lösungen als n-te Einheitswurzeln. Die Bezeichnung „Kreisteilungsgleichung“ erklärt sich, wenn man ihre Lösungen in der Gaußschen Ebene betrachtet: die n-ten Einheitswurzeln teilen den Kreis mit dem Radius 1 und dem Koordinatenursprung als Mittelpunkt in n gleiche Teile, sie bilden die Eckpunkte eines in den Kreis einbeschriebenen regulären n-Ecks.
Anders als bei reellen Zahlen kann man nicht so einfach eine der Wurzeln als die Wurzel auszeichnen; dort wählt man die einzige nichtnegative Wurzel. Man kann jedoch eine (holomorphe) n-te Wurzelfunktion für komplexe Zahlen, die keine nichtpositiven reellen Zahlen sind, über den Hauptzweig des komplexen Logarithmus definieren:
Man kann den Logarithmus auch (unstetig) auf die negative reelle Achse fortsetzen, es gilt dann aber mit der so definierten Wurzelfunktion beispielsweise
![\sqrt[3]{-8} = 2\,\exp{(\mathrm{i}\,60^\circ)} = 1+\mathrm i\sqrt3](/pictures/dewiki/99/c364f50bbea6113f78347bf09478af66.png) und nicht = − 2.
und nicht = − 2.Literatur
- Ulrich Felgner: Über den Ursprung des Wurzelzeichens. In: Mathematische Semesterberichte. Bd. 52, Nr. 1, 2005, Springer, S. 1–7, ISSN 0720-728X (doi:10.1007/s00591-004-0083-4)
- Hans Kreul, Harald Ziebarth: Mathematik leicht gemacht, Verlag Harri Deutsch, 6. Auflage 2006. Das komplette Kapitel zur Wurzelrechnung mit Erklärungen, Beispielen und Aufgaben ist kostenlos online abrufbar. ISBN 978-3-8171-1786-4.
Weblinks
Wikimedia Foundation.

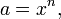
![x = \sqrt[n\,]{a}](/pictures/dewiki/48/0876fe91578ac0d09c102c6f8a07f315.png)
![\sqrt[3]{8} = 2 \Leftrightarrow 2^3 = 8](/pictures/dewiki/54/671f32d5267b97b2b9a0b75aa6f80707.png)



![(\sqrt[n]{a})^n = a \quad \forall\ a \geq 0, n \geq 1\,.](/pictures/dewiki/53/5df584a30c0c406c4a025c47ad7b0840.png)
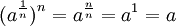
![\sqrt[n]{a} = a^{\frac{1}{n}}](/pictures/dewiki/101/ec88827417db352f94755f7f655c012e.png)
![\sqrt[2n]{x^{2n}} = |x|\,.](/pictures/dewiki/97/a326bb14da76bfbf6fe629a6c5c91198.png)
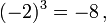
![-2=\sqrt[3]{-8}\ne\sqrt[6]{(-8)^2}=\sqrt[6]{64}=+2.](/pictures/dewiki/97/a948200eec48978bb74576dd018089b6.png)
![\sqrt[n]{a}\cdot\sqrt[n]{b}=\sqrt[n]{a\cdot b}](/pictures/dewiki/55/73d577cd0a118df1dda404e72e4a922d.png)
![\sqrt[m]{\sqrt[n]{a}}=\sqrt[m\cdot n]{a}](/pictures/dewiki/48/0a8209eed9a856af2b508dedfad9ffee.png)
![\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}](/pictures/dewiki/56/81a910073a5639512945a6d1e8e0d102.png)
![\left(\sqrt[n]{a} \right)^m=\sqrt[n]{a^m}](/pictures/dewiki/97/a852c0aa9734b397b1bd4b3a122b7f11.png)
![a^{\frac{m}{n}}=\sqrt[n]{a^m}](/pictures/dewiki/52/43edac46411a2ae56ea7d55ac06fa113.png)
![a^{-\frac{m}{n}}=\frac{1}{\sqrt[n]{a^m}}](/pictures/dewiki/50/218245090feab2ff8a5d8ecf674fd7e1.png)
![\sqrt[n]{x} = x^{1/n} = \exp\left(\frac{\ln(x)}{n}\right)](/pictures/dewiki/98/b19b85199a4fa580acec9c4e1717b4ed.png)
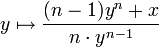
![z_k=\sqrt[n]{|a|}\cdot\exp\left(\frac{\mathrm i\varphi}{n} + k\cdot\frac{2\pi\mathrm i}{n}\right)\quad(k=0,1,\dots,n-1) .](/pictures/dewiki/97/a8cfcf27e2940949fc1e0003313987a6.png)