- Zauberwürfel
-
Der Zauberwürfel (oft auch wie im englischsprachigen Raum Rubik’s Cube genannt) ist ein mechanisches Geduldsspiel, das vom ungarischen Bauingenieur und Architekten Ernő Rubik erfunden wurde und 1980 mit dem Sonderpreis Bestes Solitärspiel des Kritikerpreises Spiel des Jahres ausgezeichnet wurde. Es erfreute sich insbesondere Anfang der 1980er Jahre bei Kindern, Jugendlichen und Erwachsenen großer Beliebtheit.
Inhaltsverzeichnis
Beschreibung
Es handelt sich dabei um einen Würfel mit einer Kantenlänge von 57,5 mm (gemessen an den Mittelachsen und in der Standardgröße), der in Höhe, Breite und Tiefe in drei Ebenen unterteilt ist, die sich durch 90-Grad-Drehungen um ihre jeweilige Raumachse zur Deckung bringen lassen. Dadurch können Position und Lage der verschiedenen Steine fast beliebig geändert werden. Auf die nach außen sichtbaren Flächen der Steine sind kleine Farbflächen geklebt. In der Grundstellung sind die Steine so geordnet, dass jede Seite des Würfels eine einheitliche, aber von Seite zu Seite unterschiedliche Farbe besitzt.
Ziel ist es für gewöhnlich, den Würfel wieder in seine Grundstellung zu bewegen, nachdem zuvor die Seiten in eine zufällige Stellung gedreht wurden. Auf den ersten Blick erscheint diese Aufgabe außerordentlich schwierig, jedoch wurden schon frühzeitig Strategien entwickelt, deren Kenntnis ein relativ leichtes Lösen gestattet.
Aufbau und Komponenten
- Mittelstein: Die sechs Steine in der Mitte der Würfelflächen sitzen auf dem Achsenkreuz im Inneren des Würfels, und besitzen daher zueinander konstruktionsbedingt immer dieselbe relative Lage. Die Farbe des Mittelsteines bestimmt, welche anderen Steine auf diese Seite gehören und welche Orientierung sie haben müssen.
- Kantenstein: Die zwölf Kantensteine verbinden je zwei angrenzende Flächen und werden von den Mittelsteinen der beiden Flächen gehalten.
- Eckstein: Die acht Ecksteine verbinden je drei angrenzende Flächen in den Ecken. Sie werden von den drei benachbarten Kantensteinen in Position gehalten.
Geschichte
In der Sendung Der große Preis erklärte der Erfinder, er habe durch ein dreidimensionales Geduldsspiel seinen Studenten eine Möglichkeit geben wollen, ihr räumliches Denkvermögen zu trainieren.
Nachdem Rubik für den Würfel am 30. Januar 1975 das Patent erteilt worden war, hielt der Würfel im Dezember 1977 Einzug in die „kapitalistische Welt“, als ein Exemplar des Würfels der im Vereinigten Königreich ansässigen Firma Pentangle zugesandt wurde. Diese Firma erwarb daraufhin die Lizenz zum Vertrieb des Würfels in Großbritannien. Die Regierung in Ungarn vergab aber 1979 die weltweiten Verkaufsrechte für den Würfel an die US-amerikanische Firma Ideal Toy Corporation. Darin waren vertragswidrig auch die Rechte für das Vereinigte Königreich enthalten. Ideal Toy Corporation erlaubte Pentangle den Verkauf des Würfels an Geschenk-, aber nicht an Spielzeuggeschäfte. Ab dem 2. Juni 1980 war er in Deutschland erhältlich.
1981 hatte die Nachfrage nach dem mechanischen Geduldsspiel ihren Höhepunkt. Ideal Toy Corporation konnte die Nachfrage nicht befriedigen, was es fernöstlichen Billigprodukten ermöglichte, den Markt zu überschwemmen. Insgesamt wurden wohl etwa 160 Millionen Würfel allein bis zum Höhepunkt des Booms verkauft. Anfang 1982 brach die Nachfrage für den Würfel ein und mit ihr auch die Nachfrage nach vielen anderen Geduldsspielen.
Ernő Rubik war nicht der erste, der sich mit dem Thema eines Spiels dieser Art beschäftigte. Schon 1957 entwickelte der Chemiker Larry Nichols einen ähnlichen Würfel, der allerdings nur aus 2×2×2 Teilen bestand und durch Magnete zusammengehalten wurde. Er ließ seinen Entwurf im Jahre 1972 patentieren. 1984 gewann Nichols eine Patentklage gegen die Firma, die den Rubik’s Cube in den USA vertrieb. Allerdings wurde dieses Urteil 1986 teilweise aufgehoben, so dass es nur noch den 2×2×2 großen Pocket Cube betraf.[1]
Auf der CeBIT 2009 wurde auch eine digitale Version des Würfels vorgestellt, welche mit Leuchtdioden und Touchfeldern ausgestattet ist.[2]
Lösungsstrategie für den Zauberwürfel
Strategien, die mit möglichst wenigen Bewegungen des Würfels auskommen, sind meist nur mit Hilfe eines Computers oder umfangreicher Stellungstabellen realisierbar. Andere, leichter zu merkende Strategien kommen mit wenigen Basiszügen aus, erfordern aber im Allgemeinen eine höhere Zahl von Bewegungen.
Algorithmen zur Lösung des Würfels werden mittels verschiedener Notationen aufgeschrieben. Der geläufigste Lösungsweg, bei der die drei Etagen des Würfels nacheinander geordnet werden, wird häufig als die Beginner-Methode bezeichnet. Sie ähneln der publizierten Lösung, die der Spiegel (Nr. 4/1981) veröffentlichte. Im Bereich Speedcubing, wo es besonders auf die Schnelligkeit ankommt, werden zur Lösung des Zauberwürfels andere Varianten angewendet, zu nennen sind Jessica-Fridrich-Methode oder die nach Lars Petrus.
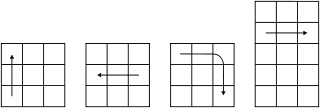
Grafische Notation
Alternativ dazu verwenden manche Anleitungen auch grafische Notationsformen, entweder als dreidimensionale Würfeldarstellungen oder als 3×3-Aufsicht der Vorderseite mit Pfeilen, die die Drehung der Würfelflächen angeben. Letztere haben den Nachteil, dass Operationen der (von vorne gesehen) mittleren und hinteren Würfelebene nur schwer darstellbar sind, z. B. durch eine zusätzliche Abwicklung der Oberseite. Ein Vorteil dieser Notation ist allerdings, dass sie Drehungen der anderen Mittelebenen als Einzelzüge darstellen kann.
Buchstabennotation
Um Zugkombinationen für den Würfel zu notieren, wird jeder Aktion ein Buchstabe zugeordnet.
Abkürzung Seite dt. engl. V F(ront) vorne H B(ack) hinten R R(ight) rechts L L(eft) links O U(p) oben U D(own) unten x x Drehung des ganzen Würfels beim Betrachten der rechten Seite y y Drehung des ganzen Würfels beim Betrachten der oberen Seite z z Drehung des ganzen Würfels beim Betrachten der vorderen Seite Ein Buchstabe bedeutet dabei stets eine Drehung um 90° im Uhrzeigersinn, ein ' oder -1 gegen den Uhrzeigersinn relativ zur gerade betrachteten Seite. So ist beispielsweise die Drehung der Unterseite um 90° im Uhrzeigersinn (D) genau entgegengesetzt zur Drehung der Oberseite um 90° im Uhrzeigersinn (U). Klein geschriebene Buchstaben, die sich auf Seiten beziehen, bedeuten die Drehung von zwei Ebenen von der entsprechenden Seite aus betrachtet; für r z. B. die rechte und dazu parallele mittlere Ebene.
Beispiel: Die folgende Kombination kippt zwei Kantensteine und lässt alle übrigen unverändert:
- K1 = B' R2 B2 R B' R' B' R2 F D B D' F'
Dabei bedeutet B' eine Drehung der hinteren Seite um 90° gegen den Uhrzeigersinn, R2 eine Drehung der rechten Seite um 180° und R eine Drehung der rechten Seite um 90° im Uhrzeigersinn.
Optimale Lösungen
Der kürzeste Weg, um den Zauberwürfel aus einer zufällig gegebenen Stellung in die Ausgangsstellung zu überführen, wird als Gottes Algorithmus (engl. God’s Algorithm) bezeichnet. Diese Formulierung stammt von dem englischen Gruppentheoretiker John Conway oder einem seiner Kollegen in Cambridge.[3] Es gibt dabei zwei Möglichkeiten, die Würfelbewegungen zu zählen: Im Allgemeinen werden komplett durchgeführte Drehungen von Seitenflächen (und nicht nur Vierteldrehungen) als ein Zug gezählt.
Den ersten Algorithmus zum Finden einer optimalen Lösung formulierte Richard E. Korf, der 1997 zeigte, dass die durchschnittliche optimale Lösung 18 Züge benötigt.[4] Er ging außerdem davon aus, dass nie mehr als 20 Züge (Gottes Zahl) erforderlich sind, jedoch konnte er das nicht beweisen. Bereits 1992 hatte Dik T. Winter eine Stellung gefunden, die 20 Züge benötigt. Den Beweis, dass diese Stellung tatsächlich nicht in weniger Zügen zu lösen ist, erbrachte Michael Reid im Jahr 1995.
Im August 2008 konnte der amerikanische Informatiker Tomas Rokicki mit gewaltigem Rechenaufwand zeigen, dass die Anzahl der Züge, die man bei richtiger Strategie maximal dazu benötigt, Rubiks Zauberwürfel aus jeder beliebigen Stellung in seine Ausgangslage zurückzudrehen, höchstens 25 sein kann,[5] was er 2010 durch verbesserte Computer-Unterstützung (durch den Software-Ingenieur John Welborn von Sony Pictures[6]) auf 22 reduzieren konnte.[7]
Im Juli 2010 bewies Tomas Rokicki zusammen mit Morley Davidson, John Dethridge und Herbert Kociemba die Vermutung, dass nie mehr als 20 Züge notwendig sind.[8]
Mathematik
Der Würfel als mathematische Gruppe
Der Würfel kann als mathematische Gruppe aufgefasst werden.
Dafür wird jede Stellung als eine Verknüpfung der sechs möglichen Basis-Permutationen
 betrachtet.
betrachtet.Alle möglichen Permutationen (Stellungen) bilden die Menge
 . Jede Stellung ist durch eine Verknüpfung der sechs Grundpermutationen
. Jede Stellung ist durch eine Verknüpfung der sechs Grundpermutationen  zu erreichen, die mit der zweistelligen Verknüpfung
zu erreichen, die mit der zweistelligen Verknüpfung  verbunden werden.
verbunden werden.Außerdem existiert sowohl ein neutrales Element, die Grundstellung i (entspricht einer „Nulloperation“ ausgeführt auf dem gelösten Würfel), denn für alle möglichen Permutationen (Gruppenelemente) p gilt
 , als auch ein inverses Element, da zu jeder Permutation p ein Element p − 1 mit
, als auch ein inverses Element, da zu jeder Permutation p ein Element p − 1 mit  existiert, zum Beispiel
existiert, zum Beispiel  oder
oder  . Weiterhin gilt für alle
. Weiterhin gilt für alle  .
.Das Tripel
 bildet daher eine Gruppe im Sinne der Algebra. Diese ist nicht kommutativ, da die Verknüpfung
bildet daher eine Gruppe im Sinne der Algebra. Diese ist nicht kommutativ, da die Verknüpfung  nicht kommutativ ist (
nicht kommutativ ist ( ).
).Lösungen des Würfels
Sei jetzt eine Permutation
 gegeben (ein verdrehter Würfel), so besteht die Aufgabe darin, eine endliche Folge (σi) von Permutationen aus der Menge
gegeben (ein verdrehter Würfel), so besteht die Aufgabe darin, eine endliche Folge (σi) von Permutationen aus der Menge  zu finden, die genau diese Permutation s erzeugt:
zu finden, die genau diese Permutation s erzeugt:Die Lösung ist nicht eindeutig, das heißt, es gibt viele Lösungen, von denen die kürzeste gesucht ist. Der Durchmesser der Gruppen, also die maximale Länge einer Permutation, mit der alle Elemente aus
 erreicht werden, ist für
erreicht werden, ist für  20.
20.Im Juni 2007 haben Gene Cooperman und Dan Kunkle von der Northeastern University in Boston gezeigt, dass 26 Züge stets ausreichen.[9] Im April 2008 hat sich diese Schranke nochmal auf 23 verringert (s.o.). Im Juli 2010 haben die drei US-Amerikaner Morley Davidson, John Dethridge und Tomas Rokicki und der Darmstädter Herbert Kociemba die minimale Anzahl von 20 endgültig gefunden. Diese Schranke ist die kleinstmögliche, die für jede Würfelstellung ausreicht.[10]
Ordnung der Gruppe G
Die Ordnung einer Gruppe
 entspricht der Mächtigkeit ihrer Trägermenge
entspricht der Mächtigkeit ihrer Trägermenge  . Da es nur eine endliche Zahl von möglichen Stellungen geben kann, entspricht diese der Anzahl der möglichen Stellungen:
. Da es nur eine endliche Zahl von möglichen Stellungen geben kann, entspricht diese der Anzahl der möglichen Stellungen: =
=  [11]
[11]
Diese ergeben sich aus
- 8 Stellen, an denen sich die Eckwürfel befinden können (8!),
- 3 Drehpositionen, die jeder Eckwürfel einnehmen kann (38),
- 12 Stellen, auf die sich die Kantenwürfel verteilen (12!),
- 2 Drehpositionen, die jede Kante einnehmen kann (212).
Der Nenner ergibt sich aus drei Bedingungen, die gelten, wenn der Würfel verdreht, aber nicht auseinandergenommen wird:
- Wenn ein Eckwürfel verdreht ist, dann ist immer eine weitere Ecke verdreht (3)
- Wenn eine Kante verdreht ist, dann ist immer eine weitere Kante verdreht (2)
- Es lassen sich weder allein zwei Eckwürfel vertauschen, noch lassen sich allein zwei Kanten vertauschen. Die Anzahl der paarweisen Zweiertäusche muss immer gerade sein (2).
Untergruppen
Wenn man die Menge der erzeugenden Permutationen begrenzt, entstehen Trägermengen mit geringerer Mächtigkeit, die Teilmengen von
 sind. Diese Untergruppen sind für das Lösen des Würfels mit Computern von entscheidender Bedeutung.
sind. Diese Untergruppen sind für das Lösen des Würfels mit Computern von entscheidender Bedeutung.Wettbewerbe
Einige Leute, die sich Speedcuber nennen, haben Strategien gefunden, die es ihnen ermöglichen, mit 45 bis 60 Bewegungen einen beliebig verdrehten Würfel zu lösen. Beim Speedcubing, also dem Lösen auf Zeit, kommt es darüber hinaus aber auch auf Fingerfertigkeit und das Verinnerlichen einer hohen Anzahl von vorgefertigten Zugfolgen an. Im Speedcubing werden Landes-, Kontinental- und Weltmeisterschaften ausgetragen.
Die erste Weltmeisterschaft, veranstaltet vom Guinness-Buch der Rekorde, fand am 13. März 1981 in München statt. Die Würfel waren 40-mal verdreht und mit Vaseline eingerieben. Gewinner der Meisterschaft war Jury Fröschl aus München mit einer Rekordzeit von 38 Sekunden.
Der aktuelle Weltrekord, aufgestellt während des Melbourne Winter Open 2011 von dem Australier Feliks Zemdegs, liegt bei 5,66 Sekunden für einen 3×3×3-Würfel.[12]
Blindfold Cubing
Demonstration: Blindlösen des 3×3×3-Würfels in 49,83 Sekunden
Eine andere bekannte Disziplin ist das sogenannte Blindfold Cubing. Dabei prägt man sich zunächst den verdrehten Zauberwürfel ein und löst ihn dann mit verbundenen Augen, ohne ihn ein weiteres Mal zu sehen. Beim Multiple Blindfold Cubing merkt man sich in der Einprägphase die Lösung mehrerer Würfel hintereinander, um sie dann alle nacheinander „blind“ zu lösen. Zur Lösung werden hier meist Methoden eingesetzt, die möglichst wenige andere Steine pro Schritt ändern. Ähnlich wie bei Gedächtnissport merkt man sich die Schrittfolge mit Hilfe eines Memoriersystems, um sie später mit verbundenen Augen in die entsprechenden Fingerbewegungen umzusetzen.
Der aktuelle Weltrekord im Blindfold Cubing liegt bei 30,90 Sekunden, aufgestellt vom Mexikaner Gabriel Alejandro Orozco Casillas am 11. Dezember 2010.[13][14]
Varianten
 Megaminx
Megaminx
 4D8-Zauberwürfel
4D8-Zauberwürfel
Es gibt einige Varianten dieses mechanischen Puzzles. Etwas schwieriger ist ein mit Bildern bedruckter Würfel, da durch die allgemein bekannten Lösungsstrategien zwar die Farbflächen an der richtigen Stelle zu liegen kommen, jedoch die mittleren Flächen nicht immer in der richtigen Orientierung. So gibt es einfachere Würfel, die aus nur zwei Ebenen in jeder Raumrichtung bestehen wie der Pocket Cube und kompliziertere Varianten, die aus vier Ebenen (Rubik’s Revenge, auch bekannt als Rubiks Rache beziehungsweise Rubik’s Master Cube), fünf Ebenen (Professor’s Cube oder 5×5×5 Cube bzw. Rubiks Wahn) oder zwei und mehr versetzt ineinander integrierten Würfeln (Rubik’s Fusion) bestehen. Auch gab es einen 2×3×3-Quader: Rubiks Magisches Domino und einen Dodekaeder: (Megaminx). Ferner gibt es Rubik-Puzzles in Tonnen- oder Pyramidenform und Bälle, ebenfalls in verschiedenen Schwierigkeitsstufen.
2005 wurde erstmals ein Würfel mit sechs Ebenen präsentiert. Der zugrundeliegende Mechanismus erlaubt auch Würfel mit bis zu elf Ebenen. Diese müssen aber tonnenförmig – die Mitten der Flächen nach außen – verzerrt werden, damit die Befestigung der Ecksteine noch vollständig innerhalb des Würfels liegt. Diese Verzerrung zusammen mit der notwendigen Größe und dem Gewicht werden dem Spieler einiges an Geschick bei der Handhabung abverlangen. Die Lösungsmethoden für diese großen Würfel benötigen keine Züge, die nicht schon vom vier oder fünf Ebenen umfassenden Würfel her bekannt sind.
Seit Juni 2008 sind auch 6×6×6- und 7×7×7-Zauberwürfel auf dem Markt.
Ein wegen seiner sternförmigen Form sehr beliebtes mechanisches Puzzle ist der 4D8-Zauberwürfel. Diese ist abgeleitet von einem Sterntetraeder, (Stella Octangula) auch Keplerstern genannt. Allerdings sind dabei seine Spitzen abgeschnitten, es verbleiben sogenannte Pyramidenstümpfe (Truncated Pyramids).
Bei Computerprogrammen, die den Zauberwürfel simulieren, lassen sich oft auch noch mehr Ebenen einstellen.
Beim Rubiks Kalender-Cube (Datumswürfel) sind die Flächen mit Zahlen und Texten versehen, aus denen sich auf der Frontfläche das aktuelle Datum mit Wochentag, Monat und Tag zusammenstellen lässt.
In Folge des Booms in den 1980er Jahren tauchten auch mechanische Puzzles auf, denen eine andere Mechanik zu Grunde lag, beispielsweise Rubik’s Magic, die Teufelstonne, Back to Square One, Rubik’s Triamid, Rubik’s Clock, Alexander’s Star oder der Zauberturm. Das mechanisch anspruchsvollste Puzzle dieser Art ist wohl das Dogic in Form eines Ikosaeders (Zwanzigflächner).
Einzelnachweise
- ↑ http://digital-law-online.info/cases/229PQ805.htm Gerichtsurteil zur Patentverletzung
- ↑ Allround-PC.com: CeBIT 2009: Digitale Version des Rubik's Cubes vorgestellt, Nachricht vom 9. März 2009
- ↑ Vgl. Jerry Slocum: The Cube. The Ultimate Guide to the World's Bestselling Puzzle. Secrets – Stories – Solutions. New York: Black Dog & Leventhal, 2009, S. 26.
- ↑ Korf: Optimal Solutions to Rubik’s Cube
- ↑ Rokicki 25 moves suffice for Rubik’s Cube, Preprint
- ↑ Spiegel, Nr.23, 2010, S.103. Homepage von Rokicki
- ↑ Rokicki: Twenty-Two Moves Suffice
- ↑ God's Number is 20
- ↑ DDJ: Neuer Weltrekord: 26 Züge reichen
- ↑ http://www.cube20.org/
- ↑ Universität Mannheim, Seminar Computeralgebra mit GAP: Rubik's Cube
- ↑ Video des 3×3×3-Weltrekordes von Feliks Zemdegs
- ↑ Offizielle WCA Blindfold Rangliste
- ↑ http://www.youtube.com/watch?v=lAcCix7EiiY Video des Weltrekordes von Alejandro Orozco
Literatur
- Matthias Stolz: Die Rückkehr des Zaubers. In: Die Zeit. Hamburg 2009, Nr. 04 (15. Jan.), S. 10–15. (Leben, Über das Comeback des Zauberwürfels, Personen und den Erfinder des Zauberwürfels. Fotos, Interviews)
Einführungen und Anleitungen
- Douglas R. Hofstadter: Vom Zauber des Zauberwürfels. In: Mathematische Spielereien. Spektrum der Wissenschaft. Heidelberg 1981, Mai, S. 16ff. (Original: Scientific American, März 1981)ISSN 0170-2971 (u. a. Anleitung zur fachgerechten Würfeldemontage, Lösungsstrategie, grafische Muster und Variationen)
- Kurt Endl: Rubik’s Rätsel des Jahrhunderts. Würfel-Verlag, Gießen 1981. ISBN 3-923210-15-9
- Josef Trajber: Der Würfel (Rubik’s Cube). Falken, Niedernhausen/Ts. 1981. ISBN 3-8068-0565-2, ISBN 3-8068-0585-7
- Josef Trajber: Der Würfel für Fortgeschrittene. Falken, Niedernhausen/Ts. 1981. ISBN 3-8068-0590-3
- Tom Werneck: Der Zauberwürfel. Heyne, München 1982. ISBN 3-453-41449-7
- Tom Werneck: Der Zauberwürfel für Könner. Heyne, München 1982. ISBN 3-453-41478-0
- Tom Werneck: Die Zauber-Kugel. Vorwort von Martin Gardner. Heyne, München 1982. ISBN 3-453-41505-1 (von Rubik autorisiertes Lösungsbuch)
Mathematik
Die folgenden Titel befassen sich mit den mathematischen Eigenschaften des Zauberwürfels, enthalten aber auch Anleitungen, die u. U. leichter nachzuvollziehen sind als die informellen Einführungen.- David Singmaster: Notes on Rubik’s Magic Cube. Enslow, Hillside NJ 1981. (klassische Studie, die 5. und letzte Auflage hat den doppelten Umfang der ersten aus dem Jahr 1979)
- Alexander H. Frey, jr., David Singmaster: Handbook of Cubik Math. Enslow, Hillside NJ 1982. (vielleicht das beste Buch zum Thema)
- Wolfgang Hintze: Der ungarische Zauberwürfel. VEB Deutscher Verlag der Wissenschaften, Berlin 1982. (teilweise angelehnt an Singmasters Klassiker)
- Christoph Bandelow: Einführung in die Cubologie. Vieweg, Braunschweig/Wiesbaden 1981. ISBN 3-528-08499-5
- Christoph Bandelow: Inside Rubik’s Cube and Beyond. Birkhäuser, Basel/Boston 1982. (erweiterte englische Fassung des Vorgenannten)
- Ernő Rubik, Tamas Varga, Gerzson Keri, Gyorgy Marx, Tamas Vekerdy: Rubik’s Cubic Compendium. English translation by A. Buvös Kocka, with an afterword by David Singmaster. Oxford University Press, London 1987. (vom Erfinder des Zauberwürfels)
- David Joyner: Adventures in Group Theory: Rubik’s Cube, Merlin’s Machine, and Other Mathematical Toys. Johns Hopkins University Press, Baltimore/Maryland 2002. (eine Einführung in die Gruppentheorie anhand des Zauberwürfels)
Weblinks
 Commons: Zauberwürfel – Album mit Bildern und/oder Videos und Audiodateien
Commons: Zauberwürfel – Album mit Bildern und/oder Videos und Audiodateien Wiktionary: Zauberwürfel – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen
Wiktionary: Zauberwürfel – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen- Weltrekorde mit dem Rubik’s Cube
- Literatur zum Schlagwort Zauberwürfel im Katalog der DNB und in den Bibliotheksverbünden GBV und SWB
- 4D8: Lösung mit Bildern, Deutsch & Englisch
Disziplinen bei Wettkämpfen der World Cube AssociationN×N×N-Zauberwürfel: 2×2×2 (Pocket Cube) | 3×3×3 (Rubik’s Cube) | 4×4×4 (Rubik’s Revenge) | 5×5×5 (Professor’s Cube) | 6×6×6 (V-Cube 6) | 7×7×7 (V-Cube 7)
Weitere Zauberwürfel: Pyraminx (Tetraeder) | Megaminx (Dodekaeder) | Back to Square One
Ableitungen: Rubik’s Magic und Rubik’s Master Magic | Rubiks Uhr
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Zauberwürfel — Zau|ber|wür|fel, der: (als eine Art Geschicklichkeits u. Geduldsspiel hergestellter) Würfel, der aus einzelnen, in drei mal drei jeweils gegeneinander verdrehbaren Schichten angeordneten kleineren Würfeln aufgebaut ist u. bei dem im zu… … Universal-Lexikon
Rubiks Zauberwürfel — Der Zauberwürfel (englisch: Rubik’s Cube) ist ein mechanisches Geduldspiel, das vom ungarischen Bauingenieur und Architekten Ernő Rubik erfunden wurde und 1980 mit dem Sonderpreis Bestes Solitärspiel der Jury „Spiel des Jahres“ ausgezeichnet… … Deutsch Wikipedia
Blindfold Cubing — Rubiks Zauberwürfel Der Zauberwürfel (englisch: Rubik’s Cube) ist ein mechanisches Geduldspiel, das vom ungarischen Bauingenieur und Architekten Ernő Rubik erfunden wurde und 1980 mit dem Sonderpreis Bestes Solitärspiel der Jury „Spiel des… … Deutsch Wikipedia
Rubik's Cube — Rubiks Zauberwürfel Der Zauberwürfel (englisch: Rubik’s Cube) ist ein mechanisches Geduldspiel, das vom ungarischen Bauingenieur und Architekten Ernő Rubik erfunden wurde und 1980 mit dem Sonderpreis Bestes Solitärspiel der Jury „Spiel des… … Deutsch Wikipedia
Rubik-Würfel — Rubiks Zauberwürfel Der Zauberwürfel (englisch: Rubik’s Cube) ist ein mechanisches Geduldspiel, das vom ungarischen Bauingenieur und Architekten Ernő Rubik erfunden wurde und 1980 mit dem Sonderpreis Bestes Solitärspiel der Jury „Spiel des… … Deutsch Wikipedia
Rubiks Cube — Rubiks Zauberwürfel Der Zauberwürfel (englisch: Rubik’s Cube) ist ein mechanisches Geduldspiel, das vom ungarischen Bauingenieur und Architekten Ernő Rubik erfunden wurde und 1980 mit dem Sonderpreis Bestes Solitärspiel der Jury „Spiel des… … Deutsch Wikipedia
Rubiks Würfel — Rubiks Zauberwürfel Der Zauberwürfel (englisch: Rubik’s Cube) ist ein mechanisches Geduldspiel, das vom ungarischen Bauingenieur und Architekten Ernő Rubik erfunden wurde und 1980 mit dem Sonderpreis Bestes Solitärspiel der Jury „Spiel des… … Deutsch Wikipedia
Rubikwürfel — Rubiks Zauberwürfel Der Zauberwürfel (englisch: Rubik’s Cube) ist ein mechanisches Geduldspiel, das vom ungarischen Bauingenieur und Architekten Ernő Rubik erfunden wurde und 1980 mit dem Sonderpreis Bestes Solitärspiel der Jury „Spiel des… … Deutsch Wikipedia
Rubik’s Cube — Rubiks Zauberwürfel Der Zauberwürfel (englisch: Rubik’s Cube) ist ein mechanisches Geduldspiel, das vom ungarischen Bauingenieur und Architekten Ernő Rubik erfunden wurde und 1980 mit dem Sonderpreis Bestes Solitärspiel der Jury „Spiel des… … Deutsch Wikipedia
Mechanische Geduldsspiele — Das bekannteste mechanische Geduldspiel: Der Zauberwürfel Mechanische Geduldspiele oder Denk oder Knobelspiele ist eine Kategorie von Rätsel Spielen, in denen die Lösung des Problems durch Manipulation des ganzen Objektes oder Teile davon… … Deutsch Wikipedia