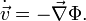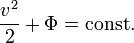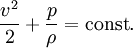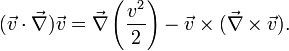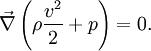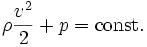- Bernoulli-Theorem
-
Als Strömung nach Bernoulli und Venturi bezeichnet man von Giovanni Battista Venturi und Daniel Bernoulli im 18. Jahrhundert entwickelte Theorien über die Strömungsmechanik, die aufeinander aufbauten, und noch heute die Grundlage für wichtige aero- und hydrodynamische Berechnungen darstellen.
Inhaltsverzeichnis
Venturi-Effekt
Der Italiener Giovanni Battista Venturi entdeckte, dass sich die Fließgeschwindigkeit eines durch ein Rohr strömenden inkompressiblen Fluids zu einem sich verändernden Rohrquerschnitt umgekehrt proportional verhält. Das heißt, die Geschwindigkeit des Fluids ist dort am größten, wo der Querschnitt des Rohres am engsten ist.
Nach dem Kontinuitätsgesetz für inkompressible Fluide tritt dieselbe Fluidmenge aus jedem beliebigen Rohrabschnitt aus, die in ihn eingeführt worden ist. Die Flüssigkeit muss die Engstelle also mit dem gleichen Durchfluss (Menge/Zeit) passieren, wie den Rest des Rohres. Deshalb muss sich die Geschwindigkeit des Fluids (Gas oder Flüssigkeit) zwingend erhöhen.Daraus alleine ergeben sich folgende zwei Fragen:
- Die Flüssigkeit, die durch ein Rohr wechselnden Querschnitts strömt, wird beschleunigt (abgebremst). Wo kommt die Kraft dazu her (siehe Newtonsche Axiome)?
- Die Flüssigkeit hat in der Engstelle des Rohres eine größere kinetische Energie als im Bereich größeren Querschnitts. Wo kommt die Energie her, ohne das Prinzip der Energieerhaltung zu verletzen?
Die Antwort hierzu führt zum Gesetz von Bernoulli.
Gesetz von Bernoulli
Daniel Bernoulli entdeckte die Beziehung zwischen der Fließgeschwindigkeit einer Flüssigkeit und deren Druck. Er fand heraus, dass in einem strömenden Fluid (Gas oder Flüssigkeit) ein Geschwindigkeitsanstieg von einem Druckabfall begleitet ist.
Herleitung aus dem Energiesatz
Der Massenpunkt im Potentialfeld
Betrachtet man einen Massenpunkt konstanter Masse m, der sich nur auf Grund eines stationären Kraftfeldes
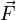 bewegt, das sich als Gradient eines Skalarpotentials
bewegt, das sich als Gradient eines Skalarpotentials 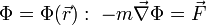 schreiben lässt, genügt er der Bewegungsgleichung:
schreiben lässt, genügt er der Bewegungsgleichung:Hier ist
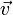 die Geschwindigkeit und
die Geschwindigkeit und 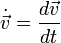 die Beschleunigung. In der klassischen Physik werden viele Prozesse mit einer Gleichung von diesem Typ beschrieben. Beispiele sind:
die Beschleunigung. In der klassischen Physik werden viele Prozesse mit einer Gleichung von diesem Typ beschrieben. Beispiele sind:- Satellitenbewegungen, hier ist Φ das Gravitionspotential und
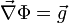 die Erdbeschleunigung
die Erdbeschleunigung - Harmonische Schwingungen, hier ist Φ das Potential aus der Rückstellkraft
- Elektrisch geladene Teilchen im elektrostatischen Feld. Φ ist das elektrische Potential des Feldes.
Auch Linearkombinationen dieser Prozesse werden durch die Bewegungsgleichung beschrieben.
Multipliziert man die Bewegungsgleichung skalar mit
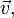 erhält man nach Integration mit der Substitutionsregel die Gleichung für die spezifische Energie:
erhält man nach Integration mit der Substitutionsregel die Gleichung für die spezifische Energie:Die Summe aus kinetischer (v2 / 2) und potentieller (Φ) spezifischer Energie ist konstant.
Die Navier-Stokes-Gleichungen
Die Bewegungsgleichung der Strömungslehre ist die Navier-Stokes-Gleichung. Für Stationarität
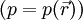 und Reibungsfreiheit (η = λ = 0) hat sie die gleiche Form wie oben allgemein. Der Druck ist hier das Skalarpotential des Kraftfeldes. Die obige Forderung nach einem Massepunkt konstanter Masse wird durch eine konstante Dichte der Strömung erreicht.
und Reibungsfreiheit (η = λ = 0) hat sie die gleiche Form wie oben allgemein. Der Druck ist hier das Skalarpotential des Kraftfeldes. Die obige Forderung nach einem Massepunkt konstanter Masse wird durch eine konstante Dichte der Strömung erreicht.Die Energiegleichung leitet sich wie oben ab und ist das Gesetz von Bernoulli:
Der Term 0,5ρv2 heißt auch dynamischer Druck oder Staudruck. Seine Summe mit dem statischen Druck p ist konstant.
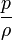 ist als Potential gleichwertig wie die Potentiale diskutiert im vorigen Abschnitt. Befindet sich die Strömung z. B. im Schwerefeld der Erde, addiert sich zu dem Gesetz von Bernoulli das Geopotential.
ist als Potential gleichwertig wie die Potentiale diskutiert im vorigen Abschnitt. Befindet sich die Strömung z. B. im Schwerefeld der Erde, addiert sich zu dem Gesetz von Bernoulli das Geopotential.Aus der Herleitung folgt, dass das Gesetz von Bernoulli für Strömungen gilt, die alle folgenden Kriterien erfüllen:
- Inkompressibilität
- Gültigkeit nur entlang einer Trajektorie (Massenpunkt)
- Stationarität (der Druck ist nur eine Funktion des Ortes)
- Reibungsfreiheit sowie keine weiteren Kräfte (z. B. Corioliskraft)
Direkte Betrachtung der Bewegungsgleichung
Die Impulsadvektion in der Navier-Stokes-Gleichung schreibt sich nach der Weber-Transformation:
Mit der zusätzlichen Annahme, dass die Strömung wirbelfrei
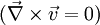 ist, wird die Navier Stokes Gleichung für stationäre, reibungsfreie Strömung konstanter Dichte:
ist, wird die Navier Stokes Gleichung für stationäre, reibungsfreie Strömung konstanter Dichte:Diese Gleichung lässt sich nun direkt entlang eines beliebigen Weges integrieren zum Gesetz von Bernoulli:
Folgerung: Ist die Strömung wirbelfrei, gilt das Gesetz von Bernoulli nicht nur entlang einer Trajektorie wie aus der Energetik abgeleitet sondern in der gesamten Strömung
Antwort auf die offenen Fragen des Absatzes Venturi-Effekt
Mit den oben stehen Herleitungen sind die offenen Fragen zu beantworten:
- Die Kraft zur Beschleunigung der Fluidteilchen in die Engstelle hinein ist die Druckgradientkraft.
- Der Energiesatz bleibt gewahrt. Die Änderung der kinetischen Energie bei Querschnittsänderung des Rohres korrespondiert mit der Änderung des Drucks als Form der potentiellen Energie.
Anwendung
Dieses Prinzip findet in unserem Alltag in vielen Dingen Anwendung. Beispiele sind:
- Die Wasserstrahlpumpe macht sich dieses Prinzip zu nutze.
- Der Ansaugtrichter eines Vergasers. Nach ihrem Erfinder sind außerdem der Venturi-Strömungsmesser und die Venturi-Düse benannt.
- Das Prandtl'sches Staurohr dient z. B. der Geschwindigkeitsmessung eines Flugzeugs. Wegen Forderung der Inkompressibilität liefert es zuverlässige Ergebnisse nur im Unterschallflug (z. B. Sportflugzeug).
- Die Umströmung einer Tragfläche genügt mit der gleichen Einschränkung dem Bernoulli-Gesetz.
Für diese Anwendungen gilt:
- Da sie keine Druckänderung entlang einer Trajektorie beschreiben, ist hierfür die Wirbelfreiheit der gesamten Strömung zu fordern.
- Das Gesetz von Bernoulli beschreibt keine Kausalität aber eine Relation zwischen Geschwindigkeits- und Druckfeld.
Siehe auch
- Bernoullische Energiegleichung
- Ausflussgeschwindigkeit (Anwendung der Bernoulli-Gleichung)
- Lavaldüse
Literatur
- G. K. Batchelor: An introduction to fluid mechanics, Cambridge university press, ISBN 0-521-66396-2
- D. Meschede (Hrsg.): Gerthsen Physik, Springer Verlag Berlin, ISBN 3540254218
Wikimedia Foundation.