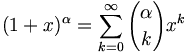- Binomialreihe
-
Die binomische Reihe ist die im binomischen Lehrsatz
auf der rechten Seite stehende Potenzreihe. Ihre Koeffizienten sind die Binomialkoeffizienten, deren Name vom Auftreten im binomischen Lehrsatz abgeleitet wurde.
Ist α ganzzahlig, so bricht die Reihe nach dem Glied k = α ab und besteht dann nur aus einer endlichen Summe. Für nicht ganzzahliges α liefert die binomische Reihe die Taylorreihe von (1 + x)α mit Entwicklungspunkt 0.
Inhaltsverzeichnis
Geschichte
Die Entdeckung der Binomialreihe für ganze positive Elemente, d. h. eine Reihenformel für Zahlen der Form (a + b)n kann heute Omar Alchaijama aus dem Jahr 1078 zugeordnet werden.
Newton entdeckt im Jahre 1669, dass die binomische Reihe für jede reelle Zahl α und alle reellen
![x\in ]-1,\,1[](/pictures/dewiki/100/dcee9d62de51b894a41c0d08ec317fd5.png) das Binom (1 + x)α darstellt. Abel betrachtete 1826 die binomische Reihe für komplexe
das Binom (1 + x)α darstellt. Abel betrachtete 1826 die binomische Reihe für komplexe  ; er bewies, dass sie den Konvergenzradius 1 besitzt, falls
; er bewies, dass sie den Konvergenzradius 1 besitzt, falls 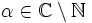 gilt.
gilt.Verhalten am Rand des Konvergenzkreises
Es sei | x | = 1 und
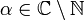 .
.- Die Reihe
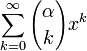 konvergiert genau dann absolut wenn Re(α) > 0 oder α = 0 ist.
konvergiert genau dann absolut wenn Re(α) > 0 oder α = 0 ist. - Für alle
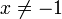 auf dem Rand konvergiert die Reihe genau dann wenn Re(α) > − 1 ist.
auf dem Rand konvergiert die Reihe genau dann wenn Re(α) > − 1 ist. - Für x = − 1 konvergiert die Reihe genau dann wenn Re(α) > 0 oder α = 0 ist.
Beziehung zur geometrischen Reihe
Setzt man α = − 1 und ersetzt x durch − x so erhält man
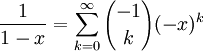 .
.Da
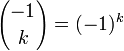 ist lässt sich diese Reihe auch schreiben als
ist lässt sich diese Reihe auch schreiben als 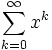 .
.Das heißt, die binomische Reihe enthält die geometrische Reihe als Spezialfall.
Beispiele

- (ein Spezialfall der ersten binomischen Formel)
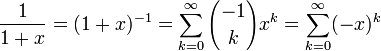
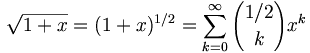
Siehe auch
Wikimedia Foundation.