- Binomische Formeln
-
Die Binomischen Formeln sind in der elementaren Algebra verbreitete Formeln zur Darstellung und zum Lösen von Quadrat-Binomen. Sie werden als Merkformeln verwendet, die zum einen das Ausmultiplizieren von Klammerausdrücken erleichtern, zum anderen erlauben sie die Term-Umformung von bestimmten Summen und Differenzen in Produkte (die Faktorisierung), was bei der Vereinfachung von Bruchtermen, beim Radizieren von Wurzeltermen sowie Logarithmenausdrücken sehr oft die einzige Lösungsstrategie darstellt.
Die Formeln gelten in allen kommutativen Ringen.
Die Bezeichnung binomisch deutet nicht auf einen Mathematiker hin, sondern erklärt sich aus der Bedeutung von bi (zwei) und Nomen (Namen) (vgl. Binom). Gleichwohl tauchen die fiktiven Alessandro Binomi und Francesco Binomi in einigen Schul- und Lehrbüchern scherzhafterweise als deren Urheber auf.
Inhaltsverzeichnis
Formeln
Allgemein:
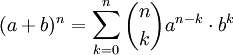 ,
, 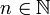
Dabei bezeichnet der Klammerausdruck den Binomialkoeffizienten.
Speziell:
-
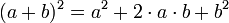
erste Binomische Formel (Plus-Formel) 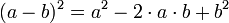
zweite Binomische Formel (Minus-Formel) 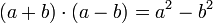
dritte Binomische Formel (Plus-Minus-Formel)
Die Gültigkeit der Formeln ist durch Ausmultiplizieren einzusehen:
Diese Formeln, häufig in der Mathematik benutzt, bieten auch eine Hilfe beim Kopfrechnen. Das Quadrat einer beliebigen Zahl zwischen 10 und 100 lässt sich oft einfach mit der binomischen Formel bestimmen, indem man die Berechnung auf Quadrate von einfacheren Zahlen (Vielfache von 10 oder einstellige Zahlen) zurückführt. Beispielsweise ist
Bei Kenntnis der Quadratzahlen bis 20 lassen sich auch viele Multiplikationen auf die dritte binomische Formel zurückführen. Beispielsweise ist
Binomische Formeln lassen sich auch für höhere Potenzen angeben, diese Verallgemeinerung ist der binomische Lehrsatz. Man benutzt dazu die Binomialkoeffizienten, die mittels des Pascalschen Dreiecks leicht zu bestimmen sind.
Auch zur dritten Binomischen Formel gibt es eine Verallgemeinerung, die einem die Faktorisierung von an - bn ermöglicht:
oder allgemein für höhere Potenzen
Eine Faktorisierung von an + bn ist ebenfalls möglich, wenn n ungerade ist, z. B.:
Für gerade n ist eine Faktorisierung von an + bn über die komplexen Zahlen möglich, z. B.:
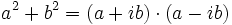 ,
,
oder, falls n auch ungerade Faktoren enthält, eine Faktorisierung in Faktoren höherer Ordnung, z. B.:
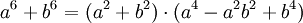 .
.
Anwendung der allgemeinen Formel
Beispiel n = 3 und b ist negativ / positiv:
Diese Formel lässt sich auch für negative Exponenten anwenden
bzw. für gebrochene Exponenten
Veranschaulichung
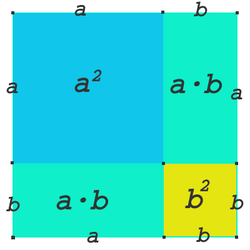
Nebenstehendes mehrfarbiges Quadrat hat die Seitenlänge (a+b). Wie sofort ersichtlich ist, passen zwei kleinere Quadrate a² und b² hinein, und es bleiben zwei Rechtecke mit der gleichen Fläche a·b übrig. Dadurch ergibt sich
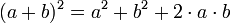
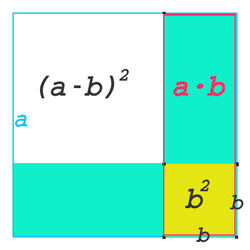
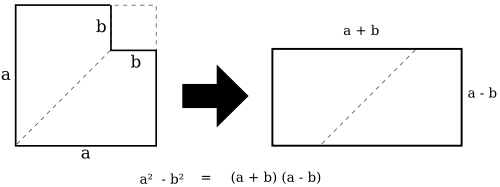
Im zweiten Bild ist a² das blau umrahmte Quadrat. Soll daraus ein Quadrat der Seitenlänge (a-b) erzeugt werden, wird zuerst die rot umrahmte Fläche a·b abgezogen. Eine ebenso große liegende Fläche kann erst abgezogen werden, wenn zuvor das kleine Quadrat b² addiert wird. Die hier gezeigte Formel lautet also
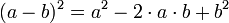
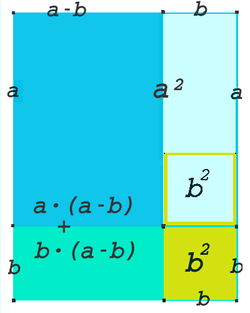
Im dritten Bild ist a² das hell- und dunkelblaue Quadrat. Wird das kleine Quadrat b² davon abgezogen und das verbleibende helle Rechteck gedreht unten angehängt, so entsteht ein Rechteck der Breite (a-b) und der Höhe (a+b). Also ergibt sich die Formel
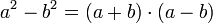
Eine weitere Veranschaulichung der dritten Binomischen Formel erhält man durch folgende Zerlegung:
Bedeutung
Mit Hilfe der Binomischen Formeln lassen sich Multiplikation und Division auf die einfacheren Rechenarten Quadrieren, Addieren, Subtrahieren, Halbieren und Verdoppeln zurückführen:
Die erste und zweite Binomische Formel liefern für das Produkt zweier Zahlen a und b:
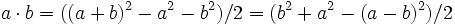
Wer an Stelle des Einmaleins die ersten hundert Quadratzahlen kennt, kann so das allgemeine Produkt zweier Zahlen leicht berechnen. In Ermangelung eines Ziffernsystems mit Null haben nachweislich die Babylonier so gerechnet und in der ganzen Antike und im Mittelalter wird man so gerechnet haben. Die angebliche Umständlichkeit der antiken Zahlsysteme wird damit relativiert, da man mit diesen Zahlsystemen sehr gut addieren und subtrahieren konnte.
Die dritte Binomische Formel ist nicht nur ein Kopfrechenkniff, sondern liefert auch ein Verfahren, die Division auf die Multiplikation und eine einfachere Division zurückzuführen. Durch Erweiterung eines Nenners a+b mit dem so genannten konjugierten a-b wird die Division durch algebraische Zahlen auf die Division von rationalen Zahlen zurückgeführt und die Division von komplexen (und hyperkomplexen) Zahlen auf die Division durch reelle Zahlen.
Siehe auch
Weblinks
Wikimedia Foundation.

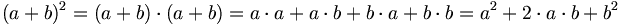
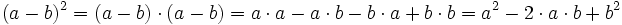
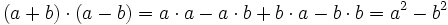
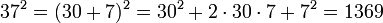
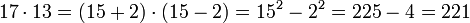
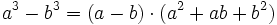
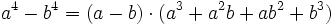
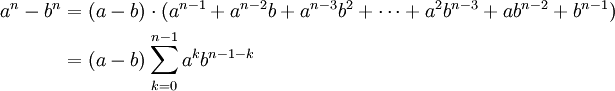
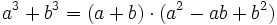
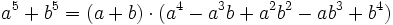
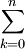 =
= 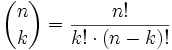 =
= 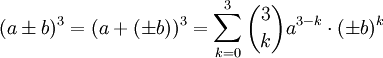
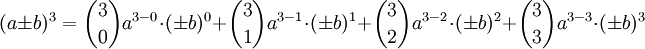
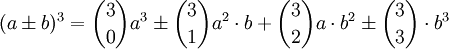
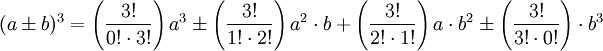
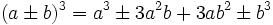
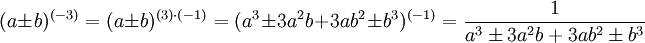
![(a \pm b)^{(\frac{3}{4})} =\sqrt[4]{(a \pm b)^{3}}=\sqrt[4]{(a^3 \pm 3 a^{2} b + 3 a b^2 \pm b^3 )}](/pictures/dewiki/57/93eb38381d0d18d9207f99c9f2244c36.png)