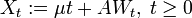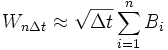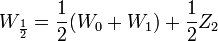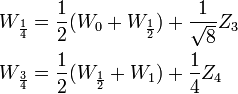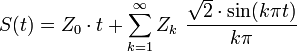- Brownian motion
-
 Zwei unabhängige Standard-Wiener-Prozesse
Zwei unabhängige Standard-Wiener-ProzesseEin Wiener-Prozess ist ein zeitstetiger stochastischer Prozess, der normalverteilte, unabhängige Zuwächse hat. Benannt wurde der Prozess, der auch als Brownsche Bewegung bekannt ist, nach dem amerikanischen Mathematiker Norbert Wiener. Seit der Einführung der Stochastischen Analysis (stochastische Integration, stochastische Differentialgleichungen) durch Itō Kiyoshi in den 1940er Jahren spielt der Wiener-Prozess die zentrale Rolle im Kalkül der zeitstetigen Stochastischen Prozesse und wird in zahllosen Gebieten der Natur- und Wirtschaftswissenschaften als Grundlage zur Simulation zufälliger Entwicklungen herangezogen.
Inhaltsverzeichnis
Definition
Ein stochastischer Prozess
 auf dem Wahrscheinlichkeitsraum (Ω,F,P), der adaptiert an die Filtrierung
auf dem Wahrscheinlichkeitsraum (Ω,F,P), der adaptiert an die Filtrierung 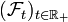 ist, heißt (Standard-)Wiener-Prozess, wenn die vier folgenden Bedingungen gelten:
ist, heißt (Standard-)Wiener-Prozess, wenn die vier folgenden Bedingungen gelten:- W0 = 0 (P-fast sicher).
- Für gegebenes s mit
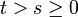 sind alle Inkremente Wt − Ws von
sind alle Inkremente Wt − Ws von 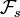 stochastisch unabhängig. Der Wiener-Prozess hat also unabhängige Zuwächse.
stochastisch unabhängig. Der Wiener-Prozess hat also unabhängige Zuwächse.  . Die Zuwächse sind also stationär und normalverteilt mit Mittelwert Null und Varianz t-s.
. Die Zuwächse sind also stationär und normalverteilt mit Mittelwert Null und Varianz t-s.- Die einzelnen Pfade sind (P-)fast sicher stetig.
Der vierte Punkt kann auch aus der Definition insofern gestrichen werden, als dass sich mit dem Stetigkeitssatz von Kolmogorow−Centsow zeigen lässt, dass es unter den obigen Voraussetzungen immer eine fast sicher stetige Version des Prozesses gibt.
Umgekehrt lässt sich ein Wiener-Prozess
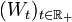 nach Lévy durch folgende zwei Eigenschaften charakterisieren:
nach Lévy durch folgende zwei Eigenschaften charakterisieren:- Wt ist ein stetiges lokales Martingal mit W0 = 0
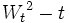 ist ein Martingal
ist ein Martingal
Eigenschaften
Einordnung
- Der Wiener-Prozess zählt zur Familie der Markow-Prozesse und dort speziell zur Klasse der Lévy-Prozesse.
- Der Wiener-Prozess ist ein spezieller Gauß-Prozess mit Erwartungswertfunktion E(Wt) = 0 und Kovarianzfunktion Cov(Ws,Wt) = min(s,t).
- Für die bedingte Erwartung gilt:
 für alle s < t, d.h.
für alle s < t, d.h.  ist ein Martingal.
ist ein Martingal. - Der Wiener-Prozess ist ein Lévy-Prozess mit stetigen Pfaden und konstantem Erwartungswert.
Eigenschaften der Pfade
- Die Pfade eines Wiener-Prozesses sind fast sicher an keiner Stelle differenzierbar und fast sicher nicht rektifizierbar.
- Die Pfade haben in jedem Intervall
![[s,t] \subset \R_{+}](/pictures/dewiki/57/912fa007e1ea33ed60b4c7dc07d138cd.png) fast sicher unendliche Variation.
fast sicher unendliche Variation. - Für die quadratische Variation gilt fast sicher < Wt > [0,t] = t.
- Über Asymptotik im Unendlichen und um den Nullpunkt geben die Gesetze des iterierten Logarithmus Auskunft.
Selbstähnlichkeiten
- Auch das Negative eines Standard-Wiener-Prozesses, also
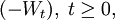 ist ein Standard-Wiener-Prozess. Allgemeiner gilt auch das Reflexionsprinzip: Ein ab einer beliebigen Stoppzeit τ gespiegelter Wiener-Prozess ist wieder ein Wiener-Prozess. Der gespiegelte Prozess
ist ein Standard-Wiener-Prozess. Allgemeiner gilt auch das Reflexionsprinzip: Ein ab einer beliebigen Stoppzeit τ gespiegelter Wiener-Prozess ist wieder ein Wiener-Prozess. Der gespiegelte Prozess 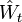 ist dabei wie folgt definiert:
ist dabei wie folgt definiert: 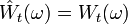 falls
falls 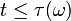 und
und 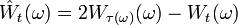 falls
falls 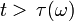 .
. - Der Wiener-Prozess ist selbstähnlich unter Streckung der Zeitachse, d.h.
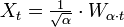 ist für jedes α > 0 ein Standard-Wiener-Prozess.
ist für jedes α > 0 ein Standard-Wiener-Prozess. - Inversion der Zeitachse: auch
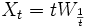 ist ein Standard-Wiener-Prozess
ist ein Standard-Wiener-Prozess - Verschiebung der Zeitachse: für jedes deterministische
 ist der stochastische Prozess Xt = Wt + s − Ws ebenfalls ein Wiener-Prozess; hier werden die Zuwächse vom Zeitpunkt s an betrachtet, d.h. W erfüllt die schwache Markow-Eigenschaft.
ist der stochastische Prozess Xt = Wt + s − Ws ebenfalls ein Wiener-Prozess; hier werden die Zuwächse vom Zeitpunkt s an betrachtet, d.h. W erfüllt die schwache Markow-Eigenschaft.
Generator
 Eine Brownsche Bewegung auf der Kugel. Der Generator dieses Prozesses ist ½ mal der Laplace-Beltrami Operator auf einer Mannigfaltigkeit, hier einer Kugeloberfläche.
Eine Brownsche Bewegung auf der Kugel. Der Generator dieses Prozesses ist ½ mal der Laplace-Beltrami Operator auf einer Mannigfaltigkeit, hier einer Kugeloberfläche.Der Generator eines eindimensionalen Wiener-Prozesses ist ½ mal der Laplace-Beltrami Operator. Damit lässt sich ein Wiener-Prozess auch auf anderen Mannigfaltigkeiten wie z.B. auf einer Kugel (siehe Bild) definieren.
Verallgemeinerter Wiener-Prozess
Ist (Wt) ein Standard-Wiener-Prozess, so nennt man den stochastischen Prozess
- Xt = μt + σWt
Brownsche Bewegung mit Drift μ und Volatilität σ. Damit lassen sich auch stochastische Prozesse darstellen, die tendenziell eher fallen (μ < 0) oder tendenziell eher steigen (μ > 0). Dabei gilt
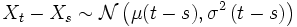 .
.Auch allgemeine Wiener-Prozesse sind Markow- und Lévy-Prozesse, aber die Martingaleigenschaft gilt nur noch in abgeschwächter Form:
Ist μ < 0, so ist Xt ein Supermartingal, ist μ > 0, so ist Xt ein Submartingal. Für μ = 0 ist Xt ein Martingal.
Der mehrdimensionale Fall
Ein mehrdimensionaler stochastischer Prozess
 heißt n-dimensionaler (standard-)Wiener-Prozess oder n-dimensionale Brownsche Bewegung, falls die Koordinaten (Wi,t) unabhängige (Standard-)Wiener-Prozesse sind. Die Zuwächse Wi,t − Wi,s sind dann ebenfalls unabhängig und
heißt n-dimensionaler (standard-)Wiener-Prozess oder n-dimensionale Brownsche Bewegung, falls die Koordinaten (Wi,t) unabhängige (Standard-)Wiener-Prozesse sind. Die Zuwächse Wi,t − Wi,s sind dann ebenfalls unabhängig und 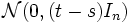 -verteilt (n-dimensionale Normalverteilung), wobei In die Einheitsmatrix der Dimension n ist.
-verteilt (n-dimensionale Normalverteilung), wobei In die Einheitsmatrix der Dimension n ist.Der n-dimensionale Wiener-Prozess hat eine besonders schöne Eigenschaft, die ihn von den meisten anderen mehrdimensionalen Prozessen abhebt und die ihn für die Modellierung des Brownschen Partikels prädestiniert: Er ist invariant unter Drehungen der Koordinatenachsen. Das bedeutet, dass für jede orthogonale Matrix
 der gedrehte (oder gespiegelte) Prozess
der gedrehte (oder gespiegelte) Prozess 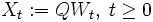 genau dieselbe Verteilung wie Wt besitzt.
genau dieselbe Verteilung wie Wt besitzt.Genau wie die eindimensionale Brownsche Bewegung kann man nun auch die n-dimensionale verallgemeinern: für jeden Vektor
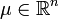 und jede Matrix
und jede Matrix  wird durch
wird durcheine Brownsche Bewegung mit Drift μ und Varianz AAT definiert. Dementsprechend gilt
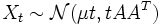 . Hierbei können die einzelnen Koordinaten also auch miteinender korreliert sein.
. Hierbei können die einzelnen Koordinaten also auch miteinender korreliert sein.Zusammenhang zu anderen stochastischen Prozessen
- Ist
 eine geometrische Brownsche Bewegung, so ist Wt: = ln(Xt) eine Brownsche Bewegung (mit Drift). Andererseits kann man aus jedem Wiener-Prozess
eine geometrische Brownsche Bewegung, so ist Wt: = ln(Xt) eine Brownsche Bewegung (mit Drift). Andererseits kann man aus jedem Wiener-Prozess  mit Drift μ und Volatilität σ durch
mit Drift μ und Volatilität σ durch 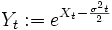 eine geometrische Brownsche Bewegung gewinnen.
eine geometrische Brownsche Bewegung gewinnen. - Mit Hilfe des stochastischen Integralbegriffes von Itô lässt sich der Wiener-Prozess zum Itō-Prozess verallgemeinern.
- Der symmetrische Random Walk kann als zeitdiskretes Pendant zum Wiener-Prozess angesehen werden, denn es gilt der folgende Konvergenzsatz: ist für
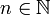 der Random Walk
der Random Walk 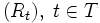 auf dem diskreten Zeitgitter
auf dem diskreten Zeitgitter 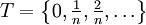 so definiert, dass R0 = 0 gilt und R sich in jedem Zeitschritt mit Wahrscheinlichkeit ½ um
so definiert, dass R0 = 0 gilt und R sich in jedem Zeitschritt mit Wahrscheinlichkeit ½ um 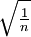 nach oben und mit Wahrscheinlichkeit ½ um
nach oben und mit Wahrscheinlichkeit ½ um 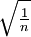 nach unten bewegt, so konvergiert R für
nach unten bewegt, so konvergiert R für 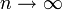 gegen einen standard-Wiener-Prozess (Invarianzprinzip von Donsker).
gegen einen standard-Wiener-Prozess (Invarianzprinzip von Donsker). - Ist
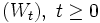 ein standard-Wiener-Prozess und T > 0, so ist
ein standard-Wiener-Prozess und T > 0, so ist 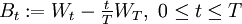 eine Brownsche Brücke.
eine Brownsche Brücke.
Geschichte des Wiener-Prozesses
1827 beobachtete der schottische Botaniker Robert Brown unter dem Mikroskop, wie Pflanzenpollen sich in einem Wassertropfen unregelmäßig hin- und herbewegten (daher der Name Brownsche Bewegung). Doch es waren nicht Naturwissenschaftler, die die Entwicklung des mathematischen Modells vorantrieben: 1880 beschrieb der Statistiker und Astronom Thorvald Nicolai Thiele (1838-1910) in Kopenhagen erstmals einen solchen „Prozess“ (die Theorie der stochastischen Prozesse war damals allerdings noch nicht entwickelt), als er wirtschaftliche Zeitreihen und die Verteilung von Residuen bei der Methode der kleinsten Quadrate studierte.
1900 griff der französische Mathematiker Louis Bachelier (1870-1946), ein Schüler Henri Poincarés, Thieles Idee auf, als er versuchte, die Kursbewegungen an der Pariser Börse zu analysieren. Beide Ansätze hatten letztendlich nur geringen Einfluss auf die zukünftige Entwicklung des Prozesses, zum Teil wohl aus dem Grunde, dass Finanzmathematik zu diesem Zeitpunkt eine untergeordnete Rolle in der Mathematik jener Zeit spielte. Heute jedoch gilt gerade die Finanzmathematik als Hauptanwendungsgebiet von Wiener-Prozessen. Dennoch bevorzugte zum Beispiel der Stochastiker William Feller die Bezeichnung Bachelier-Wiener-Prozess.
Der Durchbruch kam jedoch, als Albert Einstein 1905 in seinem annus mirabilis [1], offenbar ohne Kenntnis von Bacheliers Arbeiten und unabhängig von ihm Marian Smoluchowski (1906), [2] den Wiener-Prozess in seiner heutigen Gestalt definierten. Einsteins Motivation war es, die Bewegung der brownschen Partikel durch die molekulare Struktur des Wassers zu erklären – ein Ansatz, der damals äußerst kontrovers war, heute aber unbestritten ist – und diese Erklärung mathematisch zu untermauern. Interessanterweise forderte er dabei eine weitere, physikalisch sinnvolle Eigenschaft, die Rektifizierbarkeit der Zufallspfade, für sein Modell nicht. Obwohl dies bedeutet, dass die Partikel in jeder Sekunde eine unendlich lange Strecke zurücklegen (was das gesamte Modell theoretisch disqualifiziert), bedeutete der einsteinsche Ansatz den Durchbruch sowohl für die molekulare Theorie als auch für den stochastischen Prozess.
Einen Beweis für die wahrscheinlichkeitstheoretische Existenz des Prozesses blieb Einstein allerdings schuldig. Dieser gelang erst 1923 dem US-Amerikanischen Mathematiker Norbert Wiener, der dabei neue Hilfsmittel von Lebesgue und Borel auf dem Gebiet der Maßtheorie ausnutzen konnte. Dennoch war sein Beweis so lang und kompliziert, dass ihn wohl nur eine handvoll Zeitgenossen verstehen konnten. Von Itō Kiyoshi ist überliefert, dass er einige seiner größten Fortschritte bei der Entwicklung des stochastischen Integrals bei dem Versuch erreichte, Wieners Arbeit nachzuvollziehen.
Letztendlich war es auch Itō, der dem Wiener-Prozess den Weg von der Physik in andere Wissenschaften ebnete: durch die von ihm aufgestellten stochastischen Differentialgleichungen konnte man die Brownsche Bewegung an mehr statistische Probleme anpassen. Bacheliers Ansatz scheiterte letztendlich daran, dass der Wiener-Prozess, unabhängig von seinem Startwert, im Laufe der Zeit fast sicher einmal negative Werte erreicht, was für Aktien unmöglich ist. Doch die durch eine stochastische Differentialgleichung abgeleitete geometrische Brownsche Bewegung löst dieses Problem und gilt seit der Entwicklung des berühmten Black-Scholes-Modells als Standard. Heute werden in praktisch allen Natur- und vielen Sozialwissenschaften brownsche Bewegungen und verwandte Prozesse als Hilfsmittel verwendet.
Simulation von Brownschen Pfaden
Um mit Hilfe von Zufallszahlen Pfade eines Wiener-Prozesses zu simulieren, stehen verschiedene Methoden zur Verfügung, die allesamt auf verschiedenen Eigenschaften des Prozesses aufbauen:
Einfacher Random Walk
Die einfachste Möglichkeit besteht darin, die oben erwähnte Konvergenz des einfachen Random Walk gegen einen Wiener-Prozess auszunutzen. Dazu muss man lediglich Bernoulli-verteilte Zufallsvariablen
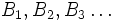 simulieren, die untereinander unabhängig sind und jeweils mit 50-prozentiger Wahrscheinlichkeit die Werte 1 und −1 annehmen. Dann kann man zu einer vorgegebenen Schrittweite
simulieren, die untereinander unabhängig sind und jeweils mit 50-prozentiger Wahrscheinlichkeit die Werte 1 und −1 annehmen. Dann kann man zu einer vorgegebenen Schrittweite  einen Wiener-Prozess an den Stellen
einen Wiener-Prozess an den Stellen  durch
durchapproximieren. Der Vorteil dieser Methode liegt darin, dass nur sehr einfach herzustellende bernoulli-verteilte Zufallsvariablen benötigt werden. Allerdings handelt es sich nur um eine Approximation: Das Resultat ist kein Gauß-Prozess, sondern hat quasi binomialverteilte Zustände (genauer gesagt ist
 binomial(n,0.5)-verteilt). Um die Normalverteilung hinreichend gut anzunähern, muss Δt deshalb sehr klein gewählt werden. Diese Methode ist deshalb nur zu empfehlen, wenn man den Prozess ohnehin auf einem sehr feinen Zeitgitter simulieren möchte.
binomial(n,0.5)-verteilt). Um die Normalverteilung hinreichend gut anzunähern, muss Δt deshalb sehr klein gewählt werden. Diese Methode ist deshalb nur zu empfehlen, wenn man den Prozess ohnehin auf einem sehr feinen Zeitgitter simulieren möchte.Gaußscher Random Walk
Die folgende Methode ist dem einfachen Random Walk überlegen (sofern kein besonders feines Zeitgitter benötigt wird), da sie den Prozess exakt simuliert (d.h. die resultierenden Zustände stimmen in Verteilung mit denen eines Wiener-Prozesses überein):
-
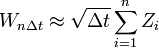 ,
,
wobei
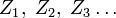 unabhängige, standardnormalverteilte Zufallszahlen sind (beispielsweise erzeugt durch die Polar-Methode von Marsaglia). Diese als Gaußscher Random Walk bezeichnete Diskretisierung ist nur dann von Nachteil, wenn die vorhandenen normalverteilten Zufallsvariablen nicht von gleichmäßiger „Qualität“ sind. Wenn zum Beispiel Quasi-Zufallszahlen verwendet werden, weisen spät auftretende Zahlen bisweilen Abhängigkeitsstrukturen auf, die das Ergebnis verzerren können. In einem solchen Fall ist eine der folgenden Methoden vorzuziehen:
unabhängige, standardnormalverteilte Zufallszahlen sind (beispielsweise erzeugt durch die Polar-Methode von Marsaglia). Diese als Gaußscher Random Walk bezeichnete Diskretisierung ist nur dann von Nachteil, wenn die vorhandenen normalverteilten Zufallsvariablen nicht von gleichmäßiger „Qualität“ sind. Wenn zum Beispiel Quasi-Zufallszahlen verwendet werden, weisen spät auftretende Zahlen bisweilen Abhängigkeitsstrukturen auf, die das Ergebnis verzerren können. In einem solchen Fall ist eine der folgenden Methoden vorzuziehen:Brownsche Brücke
Diese Methode (die nur am Rande etwas mit dem gleichnamigen stochastischen Prozess zu tun hat) nutzt die Kovarianzstruktur des Wiener-Prozesses aus und legt ein höheres Gewicht auf frühe standardnormalverteilte Zufallsvariablen
 .
.Hier wird zuerst W1, welches normalverteilt mit Varianz 1 ist, durch W1 = Z1 simuliert. Nun wird das Intervall [0,1] schrittweise halbiert und folgender Schritt wiederholt:
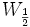 ergibt sich als arithmetisches Mittel
ergibt sich als arithmetisches Mittel 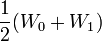 plus eine weitere Normalverteilte Zufallsvariable, um die Varianz zu korrigieren. Also:
plus eine weitere Normalverteilte Zufallsvariable, um die Varianz zu korrigieren. Also:Analog:
und so weiter. Die Faktoren
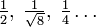 verringern sich dabei in jedem Halbierungsschritt um den Faktor
verringern sich dabei in jedem Halbierungsschritt um den Faktor 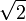 und sorgen dafür, dass die Zustände die richtige Varianz erhalten.
und sorgen dafür, dass die Zustände die richtige Varianz erhalten.Um einen Wiener-Prozess statt auf [0,1] auf ein beliebiges Intervall [0,a] auszuweiten, kann man nun die oben beschriebene Transformation
 anwenden; X ist dann ein Wiener-Prozess auf [0,a].
anwenden; X ist dann ein Wiener-Prozess auf [0,a].Spektralzerlegung
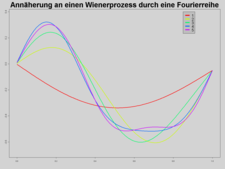
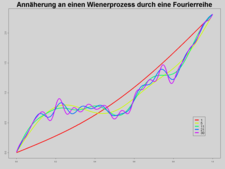
Bei der Spektralzerlegung wird der Wiener-Prozess in einer Art stochastischer Fourieranalyse als trigonometrische Polynome mit zufälligen Koeffizienten approximiert. Sind
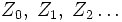 unabhängig und standardnormalverteilt, so konvergiert die Reihe
unabhängig und standardnormalverteilt, so konvergiert die Reihegegen einen Wiener-Prozess. Diese Methode konvergiert bezüglich der
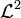 -Norm zwar mit maximaler Geschwindigkeit, beinhaltet aber im Gegensatz zur brownschen Brücke viele aufwändige trigonometrische Funktionsauswertungen. Daher findet sie, vor allem in der Monte-Carlo-Simulation, weniger oft Anwendung.
-Norm zwar mit maximaler Geschwindigkeit, beinhaltet aber im Gegensatz zur brownschen Brücke viele aufwändige trigonometrische Funktionsauswertungen. Daher findet sie, vor allem in der Monte-Carlo-Simulation, weniger oft Anwendung.Annäherung an einen Wiener-Prozeß durch Fourierreihe Geometrie
Die ein- und zwei-dimensionale Brownsche Bewegung ist rekurrent, in allen höheren Dimensionen ist sie transient. (Pólya: „Ein betrunkener Mann findet immer heim, ein betrunkener Vogel nicht.“) Siehe auch Markow-Kette.
Quellen
- ↑ Einstein, Albert: Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen.. In: Annalen der Physik. 17, 1905, S. 549-560.
- ↑ Smoluchowski, M.: Zur kinetischen Theorie der Brownschen Molekularbewegung und der Suspensionen. In: Annalen der Physik. 21, 1906, S. 756-780.
Literatur
- Andrei N. Borodin, Paavo Salminen: Handbook of Brownian Motion - Facts and Formulae, Birkhäuser, Basel 2002, ISBN 3-7643-6705-9
- Ioannis Karatzas, Steven E. Shreve: Brownian Motion and Stochastic Calculus (Graduate Texts in Mathematics), Springer, New York 1997, ISBN 0-3879-7655-8
- Bernt Øksendal: Stochastic Differential Equations. An Introduction with Applications, Springer Berlin 2003, ISBN 3-540-04758-1
- Philip E. Protter: Stochastic Integration and Differential Equations, Springer, Berlin 2003, ISBN 3-540-00313-4
- John Michael Steele: Stochastic Calculus and Financial Applications, Springer, New York 2000, ISBN 0-387-95016-8
Siehe auch
Ornstein-Uhlenbeck-Prozess, Brownsche Brücke, Stochastische Differentialgleichung, Wurzel-Diffusionsprozess, geometrische Brownsche Bewegung
Wikimedia Foundation.